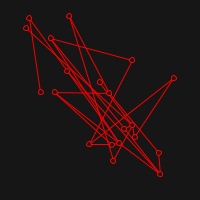
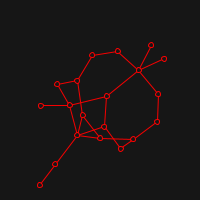
This implementation is not focused on performance, but in experimenting with this relatively simple algorithm, and visualising its process.
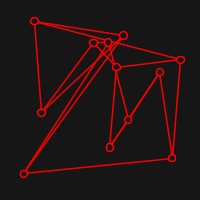
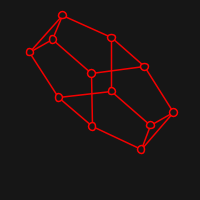
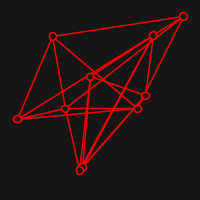
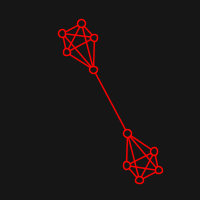
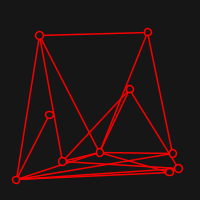
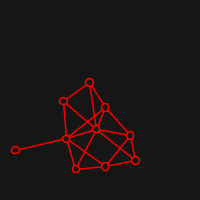
The idea of a Graph drawing is simply to take a graph and display it on a screen in a "pleasing" way whatever this means. The way that Fruchterman and Reingold approach this, is to think vertices as particles in space that exert repulsive force to the others and attractive force to the ones that are connected by some edge.
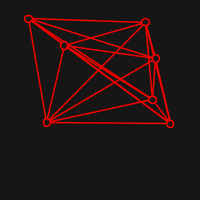
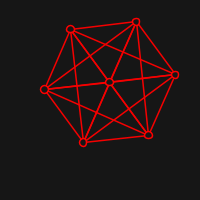
Live visualisation is implemented with quil. Here are some examples of starting positions (random) and resulting ones:
Execute with
lein run
In order to try out other graphs is likely that you only need to change some of the following lines of core.clj:
(def W 600)
(def H 600)
(def line-weight 3)
(def node-radius 15)
(defn setup []
(q/ellipse-mode :center)
(q/frame-rate 60)
{:states (al/fruchterman-reingold g/Durer (- W 30) (- H 30) 0.7)
;; We need to make with and height a little smaller since in the actual drawing
;; points have area i.e are not really points
:i -50})W (width), H (height), line-weight, node-radius and frame-rate all
explain themselves. The first of the al/fruchterman-reingold arguments
is the graph (undirected) to be drawn, to exemplify how is that we represent
graphs, here's the complete graph of three vertices:
{:V #{:a :b :c}
:E #{#{:a :b} #{:a :c} #{:b :c}}}You can either try out some of the graphs in graphs.clj or create your own. In the later case some important observations are that the graph must be connected and that the elements do not need to be keywords, since we are only interested in the structural properties of a graph and not its content.
The last argument (0.7 as default) is the ideal edge length coefficient C.
Fruchterman and Reingold approximate the ideal length of edges as C*sqrt(W*H/|V|),
in some cases if we set C too small the graph will look too dense, and if we
set it too large It will run out of space.