有很多计算机程序设计语言可以用来完成计算实习。本文章采用数学软件MATLAB来解决数学实习题,习题解答包括主程序、程序调用命令和程序执行结果三个部分。
-
用二分法求下列方程的一个近似解(精确到小数点后第六位)
(1)
$x^3+3x-5=0,x^* \in [1,2]$ ;(2)
$x= e^{-x}, x^* \in [\frac12, \ln 2]$ ;(3)
$x^2 = \cos x, x^* \in [\frac{\pi}4,\frac{3\pi}4]$ ;(4)
$7x^2-3x+\frac4x-30=0,x^* \in [2,2.5]$ .
解: 二分法主程序(bisect.m)
-
用Newton法求下列方程的近似解(精确到小数点后第10位)
(1)$x^3-x+4=0$;
(2)$x^2+\frac {1}{x^2} = 10x$
$(x>1)$ ;(3)$x\lg x = 1$;
(4)$x+e^x = 0$
(5)$\frac x2= \sin x$
$(x>0)$
解:Newton法主程序(Newton.m)
-
用Newton法导出计算机上求$A^{\frac1x}$(
$A>0$ ,n为非零整数)和$\frac1A$的算法(即只用加、减、乘三种运算的算法),并实际计算下列各值:(1)$\sqrt[3]{2}$;
(2)$\frac1{\sqrt[5]{9}}$;
(3)$\frac17$;
(4)$\frac1{11}$;
解:设$f(x)=x^n-A$,$f'(x)=nx^{n-1}$,迭代公式为$$x_{k+1}=x_{k}-\frac{x^n_k-A}{nx^{n-1}_k}=\frac{n-1}{n}x_k+\frac{A}{nx^{n-1}_k};$$
开n次方的Newton法程序代码(Newton1.m)
- 当$\epsilon=0.2$时,计算Kepler方程$$y= x-\epsilon\sin y=0 (0<\epsilon<1)$$ 对应于$x=\frac{k}{8} (k=1,2,...,8)$的y的近似值.
解:
k=1时,
 k=2时,
k=2时,
 k=3时,
k=3时,
 k=4时,
k=4时,
 k=5时,
k=5时,
 k=6时,
k=6时,
 k=7时,
k=7时,
 k=8时,
k=8时,
 5. 求方程$\tan x=x$的最小的三个正根,精确到$10^{-12}$.
5. 求方程$\tan x=x$的最小的三个正根,精确到$10^{-12}$.
解:首先粗略估计三个正根为4.4,7.6和10.9,然后带入计算。

- 求方程$\cot x = \frac{1}{x} - \frac{x}{2}$的两个正根,精确到$10^{-12}$.
解:显然,方程有无穷多个正根,粗略估计两个最小的正根为2和6,带入程序计算。

-
利用
$\pi= \displaystyle \int^{1}_{0}{\frac{dx}{1+x^2}} $ ,$π = 3.141592653589793238462643...$(1)用普通的梯形公式、Simpson公式和Cotes公式,计算圆周率$\pi$的近似值并与精确值加以比较;
(2)将区间[0,1]分成4、8等分,用复化梯形公式和复化Simpson公式计算$\pi$的近似值,并与精确值比较;
(3)用Romberg方法计算$\pi$的近似值,使它的精度达到O(
$10^{-8}$ );(4)分别用n=1,2,3,4的Gauss-Legendre公式计算$\pi$的近似值,并与前面的计算结果进行比较。
解:
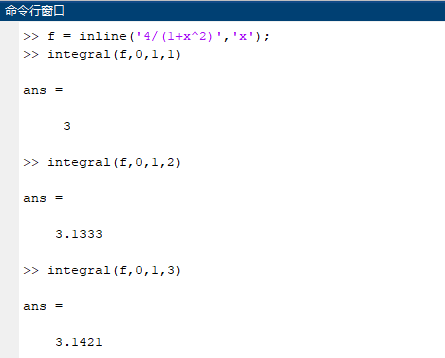
(1)
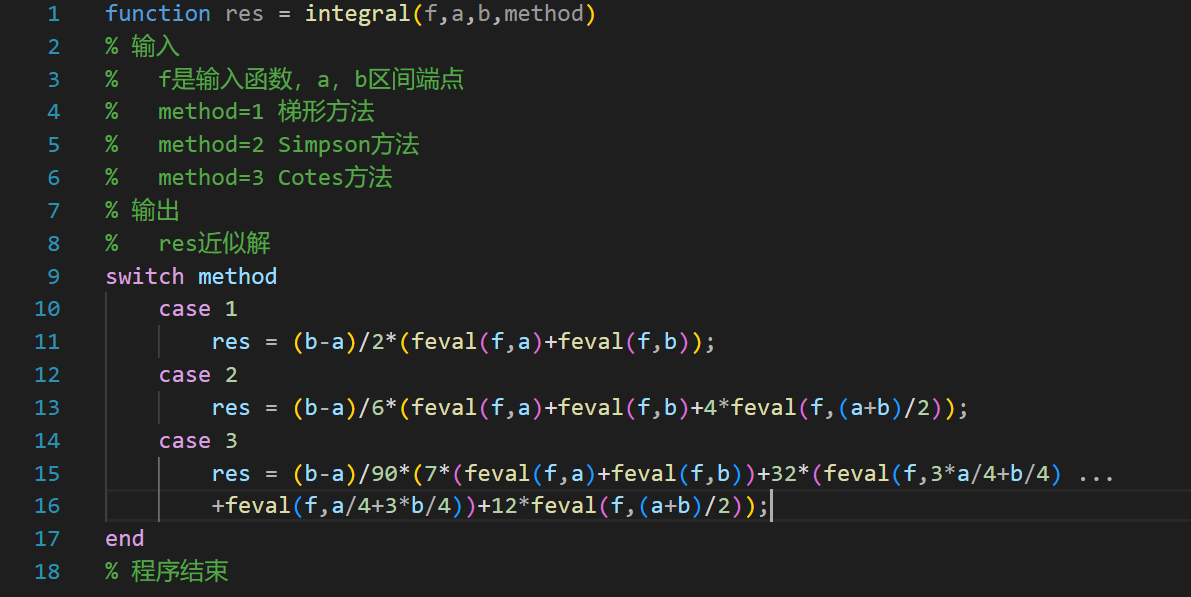
主程序(integral.m)
Cotes公式精度最高,Simpson公式其次,梯形公式最低。
(2)
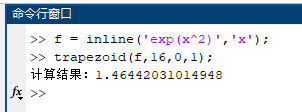
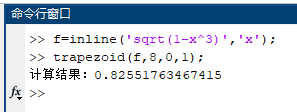
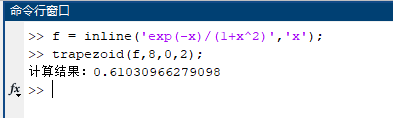
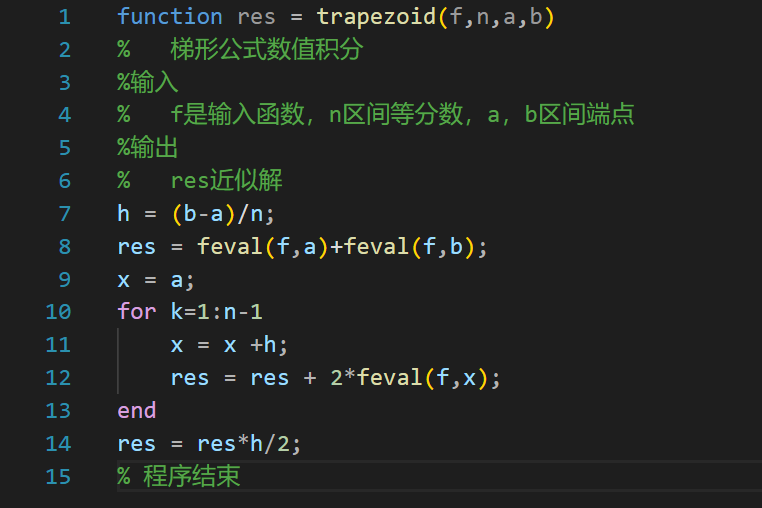
复化梯形公式主程序(trapezoid.m)
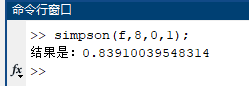
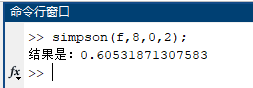
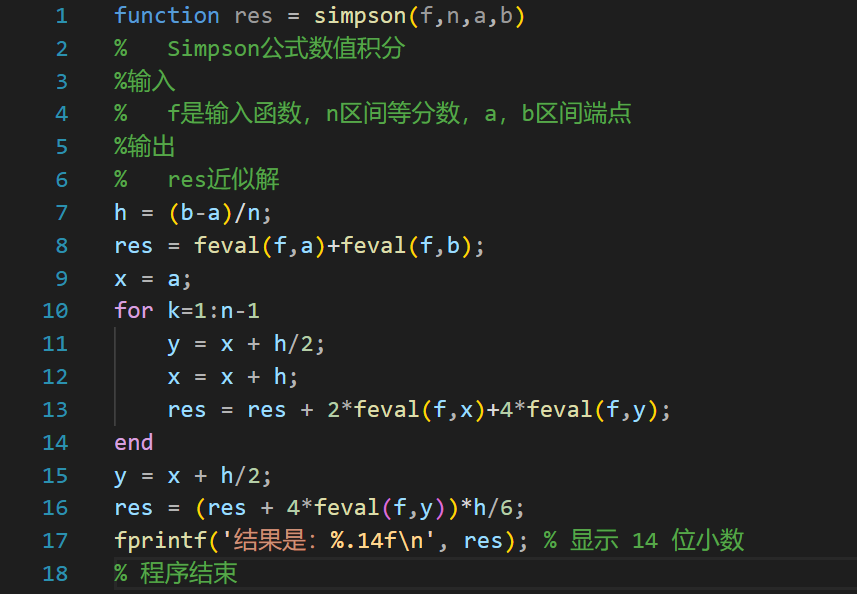
 复化Simpson公式主程序(simpson.m)
复化Simpson公式主程序(simpson.m)
 分别代入n=4和n=8,计算结果如下:
分别代入n=4和n=8,计算结果如下:
n=8时比n=4时计算精度更高,Simpson公式计算精度比梯形公式高得多。
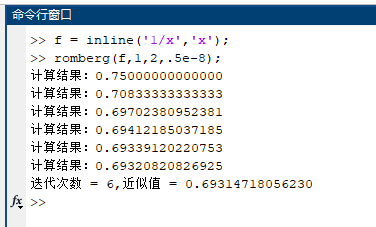
(3)
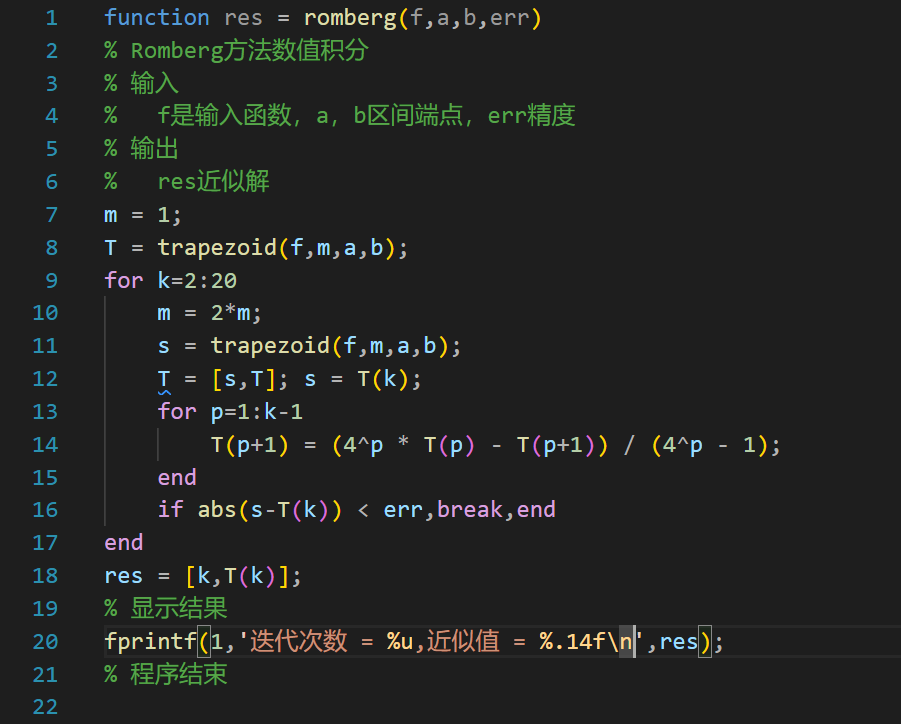
Romberg方法计算数值积分主程序(romberg.m)
计算结果:
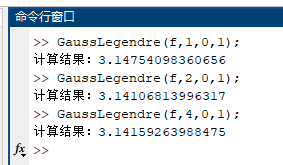
(4) Gauss-Legendre公式主程序(GaussLegendre.m)
分别使用n=1,n=2,n=4代入计算可得:
在n值相同的情况下,Gauss-Legendre公式的精确度比复化Simpson公式还要精确。
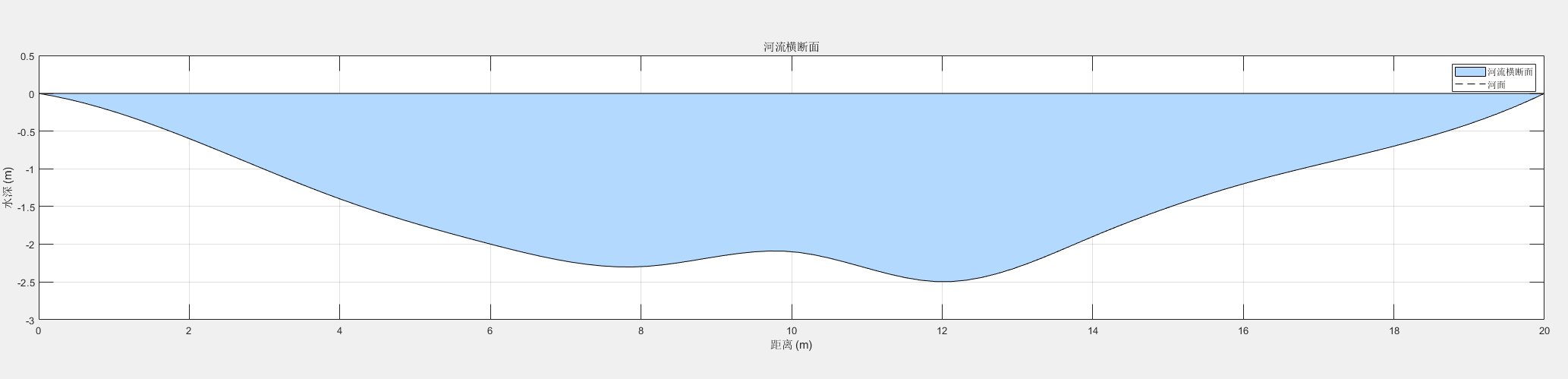
- 设河面宽20m,从河的一岸向另一岸每隔2m测得的水深(单位:m)如下:
| x | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| y | 0 | 0.6 | 1.4 | 2.0 | 2.3 | 2.1 | 2.5 | 1.9 | 1.2 | 0.7 | 0 |
求河流的横断面积。
解:使用复化梯形公式,a=0,b=20,n=10。程序如下:
x = 0:2:20;
y = [0, 0.6, 1.4, 2.0, 2.3, 2.1, 2.5, 1.9, 1.2, 0.7, 0];
A = y(1)+y(11);
for k=2:10
A = A + y(k)*2;
end
A = A*2/2
-
分别用复化梯形公式和复化Simpson公式计算下列积分:
(1)$\displaystyle \int^{1}_{0}{e^{x^2}dx},m=16$;
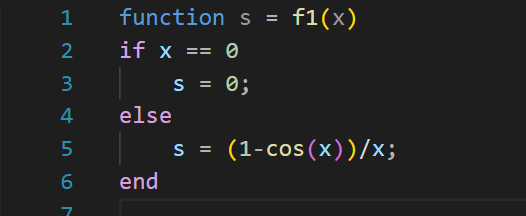
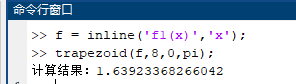
(2)$\displaystyle \int^{\pi}_{0}{\frac{1-cosx}{x}dx},m=8$; (可看成连续函数$ f(x) = \begin{cases} \frac{1-cosx}{x} & \ x \neq 0, \ 0 & \ x = 0. \end{cases} $的积分)
(3)$\displaystyle \int^{1}_{0}\sqrt{1-x^3}dx,m=8$;
(4)$\displaystyle \int_{0}^{2} \frac{e^{-x}}{1+x^2}dx,m=8$.
解
(2) 定义函数
复化梯形公式
复化Simpson公式
(3) 复化梯形公式
复化Simpson公式
(4) 复化梯形公式
复化Simpson公式
- 用Romberg计算$\displaystyle \int^{2}_{1}\frac{dx}{x}$,精确到小数点后第8位.
解
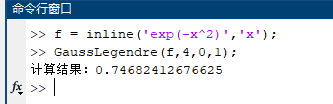
- 用一般的积分区间上的Gauss-Legendre公式(取n=4)计算积分$\displaystyle I(N)=\int^{N}_{0}{e^{-x^{2}}}dx$:
(1)$N=1$;
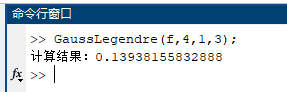
(2)$N=3$;
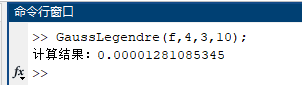
(3)$N=10$.
并与$\lim_{x \to \infty} \displaystyle \int^{N}_{0}e^{-x^{2}}dx= \frac{\sqrt{\pi}}{2}$的结果相比较。
解
于是[0,3]上积分近似于前两段积分之和0.88620568509513,[0,10]上积分近似于三段积分之和0.88621849594859,而$\sqrt{\pi}/2\approx0.886227$,精确到小数点后5位。
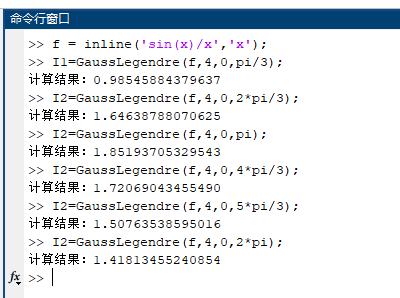
- 按照第3题(2)同样的观点,计算
解:
定义函数后,利用Gauss-Legendre公式,取n=4,依次代入k=1,2,3,...,6进行计算。
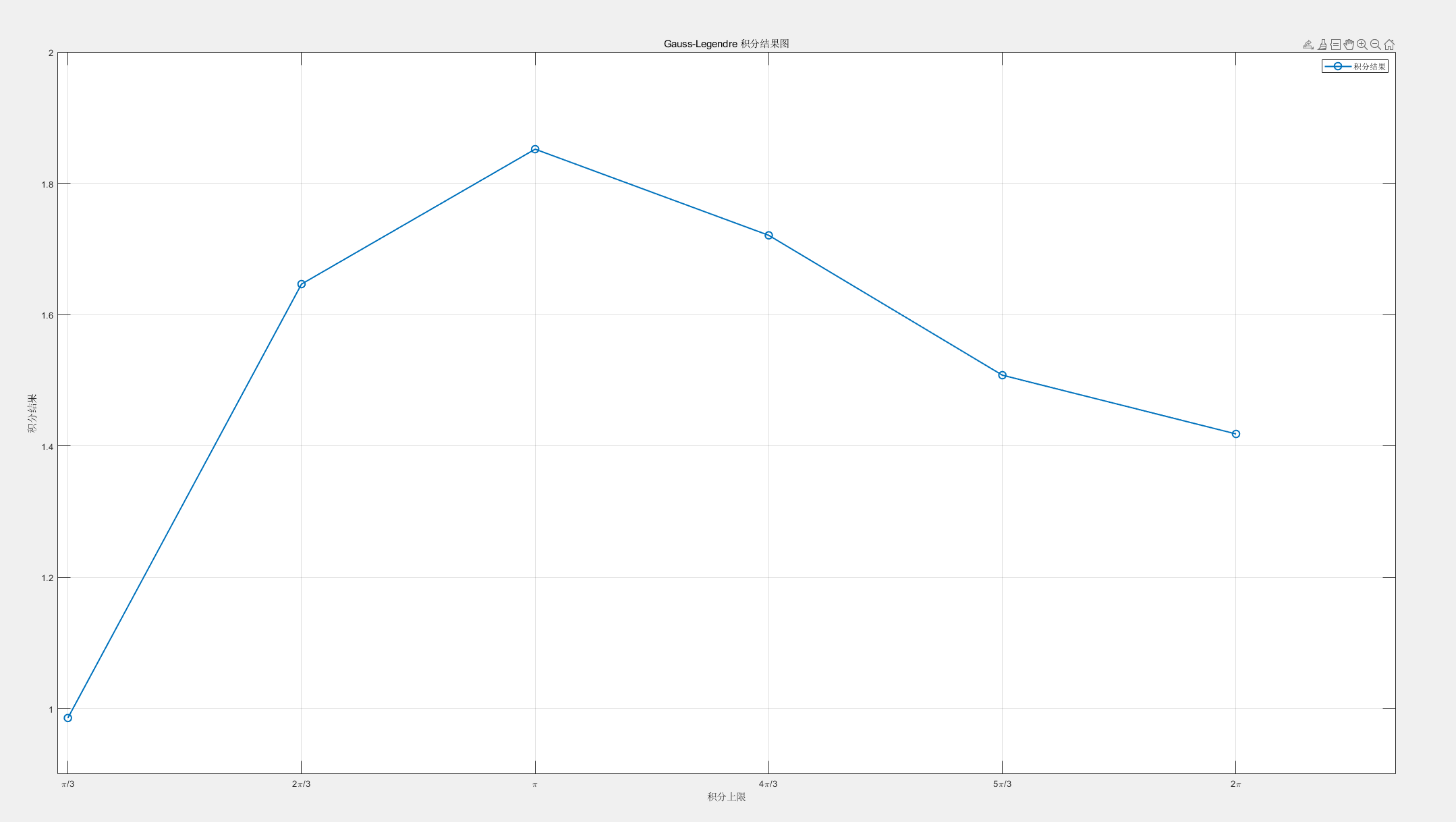
- 试编制一个通用的Gauss-Legendre求积公式程序,在计算机上实际计算下列反常积分值,并与精确值比较:
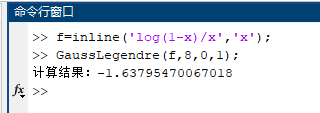
(1)$\displaystyle \int^{1}_{0}\frac{ln(1-x)}{x}dx$, 精确值$-\frac{\pi^{2}}{6}$;
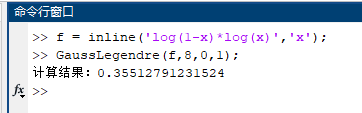
(2)$\displaystyle \int^{1}_{0}\ln x\ln(1-x)dx$, 精确值$2-\frac{\pi^{2}}{6}$;
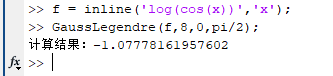
(3)$\displaystyle \int^{+\infty}_{0}\ln \cos xdx$, 精确值$-\frac{\pi}{2}\ln 2$;
(4)$\displaystyle \int^{1}_{0}\frac{\sin x}{x}dx$, 精确值$\frac{\pi}{2}$;
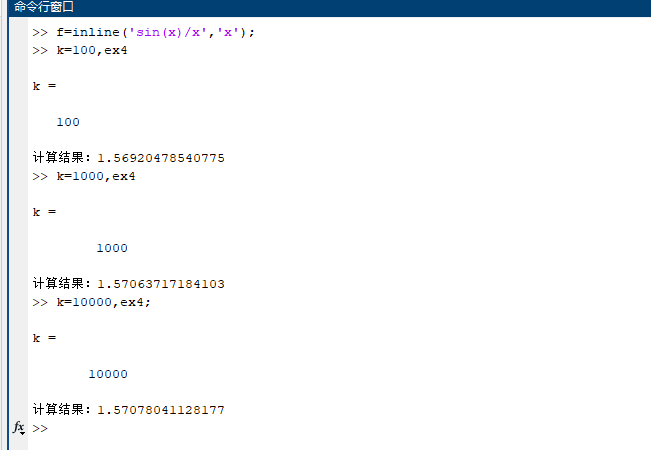
由于积分收敛较慢,根据Gauss-Legendre公式计算特点,取n=8,并将积分分段计算再求和,编写程序如下(ex4.m)
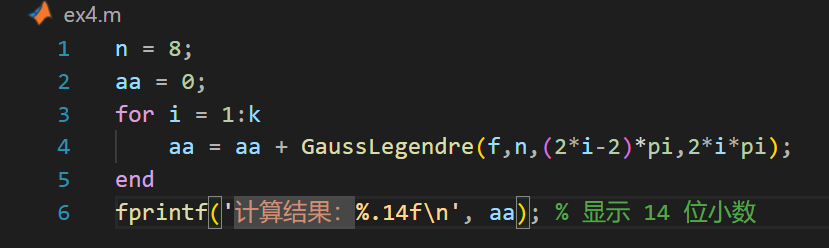
积分近似值:1.57079632679490,积分上限A计算到$20000\pi$时可得到较高的精度。
(5)$\displaystyle \int^{+\infty}_{0}\sin (x^{2})dx$, 精确值$\frac{1}{2}\sqrt{\frac{\pi}{2}}$.
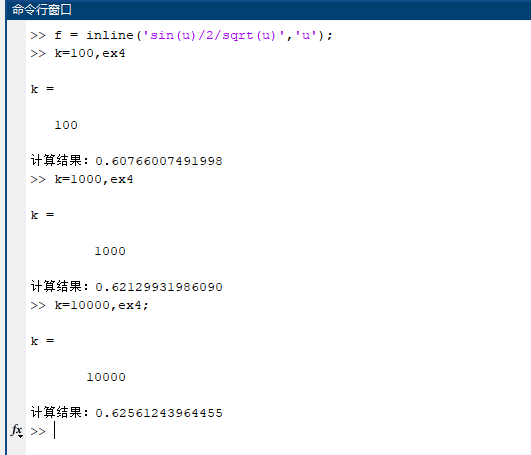
作变量代换,$u=x^{2}$, 则$dx = \frac{1}{\sqrt{u}}du$,积分化为$\displaystyle \int^{+\infty}_{0}\frac{\sin u}{2\sqrt{u}}du$
利用上一小题方法计算如下:
积分近似值0.62665706865775,可以看出积分上限A计算到$2000\pi$时得到的结果精确度不高,这是由于原积分收敛速度较慢的原因。
- 某种机器零件的加工需经两道工序,x表示零件在第一道工序中出现的疵点数(疵点指气泡、砂眼、裂痕等),y表示在第二道工序中出现的疵点数.某日测得8个零件的x与如下:
| x | 0 | 1 | 3 | 6 | 8 | 5 | 4 | 2 |
|---|---|---|---|---|---|---|---|---|
| y | 1 | 2 | 2 | 4 | 4 | 3 | 3 | 1 |
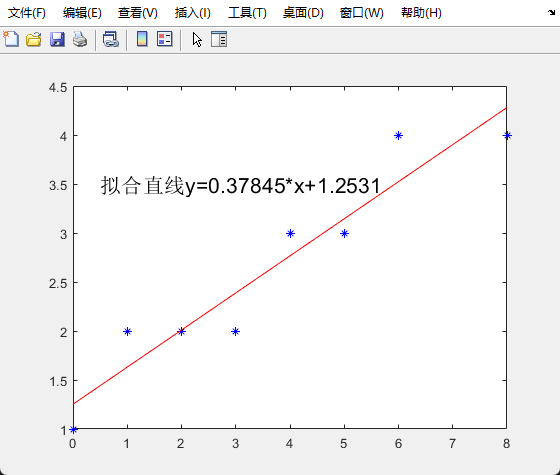
画出这些数据的散点图,找出它们之间关系的经验公式y=ax+b,并画出拟合曲线。
解: 程序代码为
hold off
x = [0,1,3,6,8,5,4,2];
y = [1,2,2,4,4,3,3,2];
plot(x,y,'b*')
hold on
A = [x',ones(size(x'))];
B = y';
x1 = A\B;
a = x1(1);b=x1(2);y=a*x+b;
plot(x,y,'r')
str = ['拟合直线y=',num2str(a),'*x+',num2str(b)];
text(0.5,3.5,str,'FontSize',16)
- 某种大豆的脂肪含量x(%)与蛋白质含量y(%)的测定结果如下表所示:
| x | 16.5 | 17.5 | 18.5 | 19.5 | 20.5 | 21.5 | 22.5 | 23.5 | 24.5 |
|---|---|---|---|---|---|---|---|---|---|
| y | 43.5 | 42.6 | 41.8 | 40.6 | 40.3 | 38.7 | 37.2 | 36.0 | 34.0 |
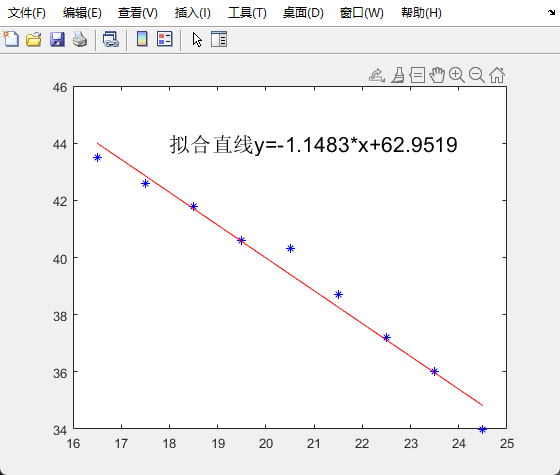
画出这些数据的散点图,找出它们之间关系的经验公式,并画出拟合曲线。 解: 程序代码如下:
hold off
x = [16.5,17.5,18.5,19.5,20.5,21.5,22.5,23.5,24.5];
y = [43.5,42.6,41.8,40.6,40.3,38.7,37.2,36.0,34.0];
plot(x,y,'b*')
hold on
A = [x',ones(size(x'))];
B = y';
x1 = A\B;
a = x1(1); b=x1(2); y=a*x+b;
plot(x,y,'r')
str = ['拟合直线y=',num2str(a),'*x+',num2str(b)];
text(18,44,str,'FontSize',16)
- 某种产品加工前的含水率(%)与加工后含水率(%)的测试结果如下表:
| 测试编号$i$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 加工前的含水率$x_i$ | 16.7 | 18.2 | 18.0 | 17.9 | 17.4 | 16.6 | 17.2 | 17.7 | 15.7 | 17.1 |
| 加工后的含水率$y_i$ | 17.5 | 18.7 | 18.6 | 18.5 | 18.2 | 17.5 | 18.0 | 18.2 | 16.9 | 17.8 |
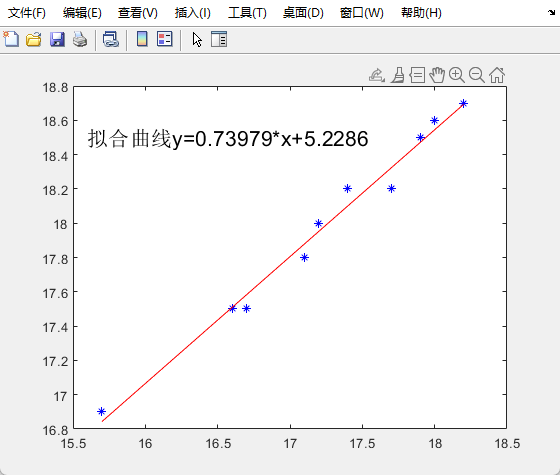
试确定加工后的含水率y与加工前含水率x的关系.
解: 程序代码为
hold off
x = [16.7,18.2,18.0,17.9,17.4,16.6,17.2,17.7,15.7,17.1];
y = [17.5,18.7,18.6,18.5,18.2,17.5,18.0,18.2,16.9,17.8];
plot(x,y,'b*')
hold on
A = [x',ones(size(x'))];
B = y';
x1 = A\B;
a = x1(1); b = x1(2); y = a*x+b;
plot(x,y,'r')
str = ['拟合曲线y=',num2str(a),'*x+',num2str(b)];
text(15.6,18.5,str,'FontSize',16)
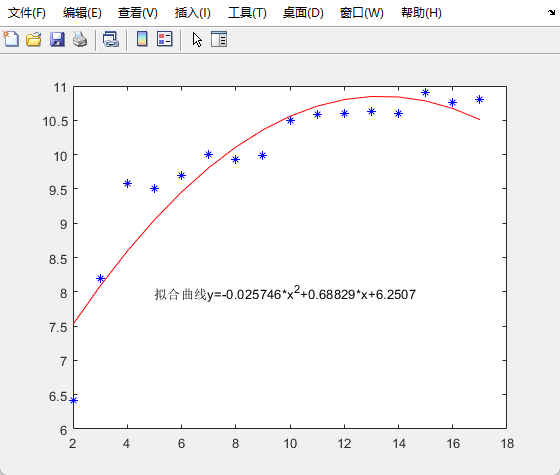
- 盛钢水的钢包,在使用过程中由于钢水对耐火材料的侵蚀,容积会不断增大.在生产过程中,积累了使用次数与钢包容积增大量之间的以下16组数据.画出这些数据的散点图,找出使用次数x与钢包容积增大量之间y之间的关系,并画出拟合曲线.
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | 6.42 | 8.20 | 9.58 | 9.50 | 9.70 | 10.00 | 9.93 | 9.99 | 10.50 | 10.59 | 10.60 | 10.63 | 10.60 | 10.90 | 10.76 | 10.80 |
解:
程序代码为
x=2:17
y = [6.42,8.20,9.58,9.50,9.70,10.00,9.93,9.99,10.50,10.59,10.60,10.63,10.60,10.90,10.76,10.80];
plot(x,y,'b*')
A=[x.^2',x',ones(size(x))']
a = A\y'
hold on
y = a(1)*x.^2+a(2)*x+a(3)
plot(x,y,'r')
str = ['拟合曲线y=',num2str(a(1)),'*x^2+',num2str(a(2)),'*x+',num2str(a(3))];
text(5,8,str)
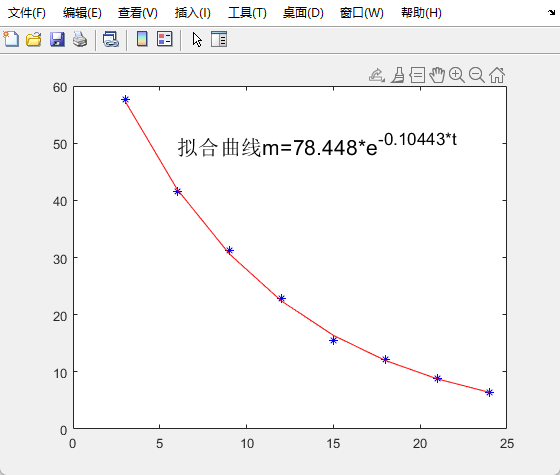
- 在研究化学反应速率时,得到下列数据.找出实验开始后的时间t与反应物的量m之间的关系,并画出拟合曲线.
| t | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
|---|---|---|---|---|---|---|---|---|
| m | 57.6 | 41.5 | 31.2 | 22.9 | 15.4 | 12.1 | 8.9 | 6.4 |
解: 程序代码为
hold off
x = 3:3:24;
y = [57.6,41.5,31.2,22.9,15.4,12.1,8.9,6.4];
plot(x,y,'b*')
hold on
y1 = log(y);
A = [x',ones(size(x))'];
a = A\y1';
y = exp(a(2))*exp(a(1)*x);
plot(x,y,'r')
string = ['拟合曲线m=',num2str(exp(a(2))),'*e^{',num2str(a(1)),'*t}'];
text(6,50,string,'FontSize',16)
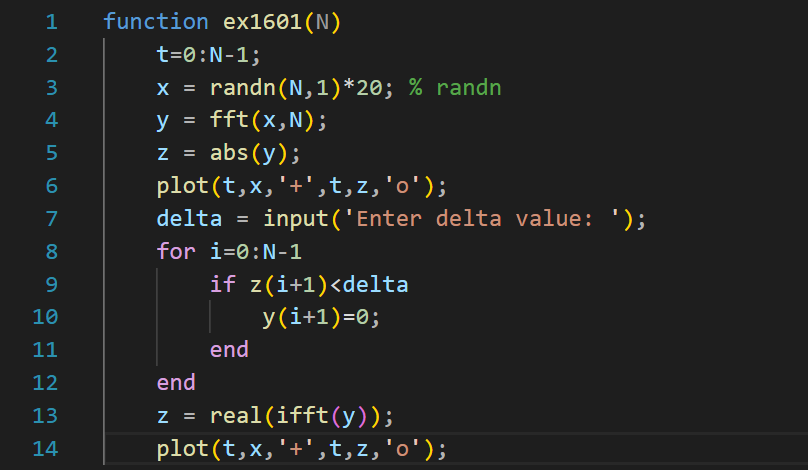
- 利用现成的数学软件,对于N=32,64,128,
(1) 生成实数序列${x(k)}_{k=0}^{N-1}$;
(2) 用快速Fourier变换(Fast Fourier Transform)计算${x(k)}{k=0}^{N-1}$的离散Fourier变换序列${X(j)}{j=0}^{N-1}$;
(3) 作出${x(k)}$和${|X(j)|}$的图并进行分析;
(4) 设定$\delta_0>0$,将${|X(j)|}<\delta_0$的数据全部置为零,再进行离散Fourier逆变换,将得到的数据与${x(k)}$比较;
(5) 改变$\delta_0$的值,重复(4),分析不同的$\delta_0$对逆变换所得到的数据的影响.
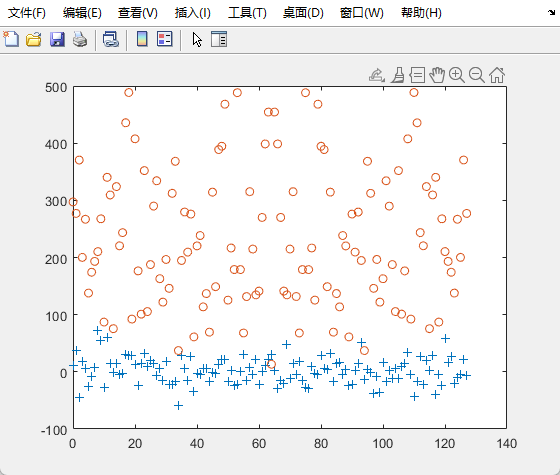
以N=128为例,运行结果如下:
本程序数据是随机产生的,“+”为原始数据,“o”为变换后的模的数据.
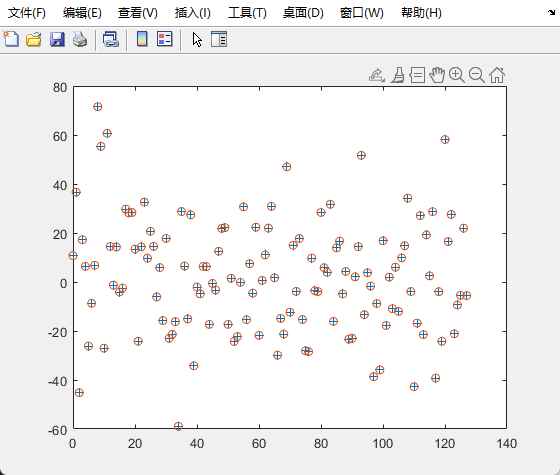
取$\delta_0 = 5$,将${|X(j)|}$中满足${|X(j)|}<\delta_0$的数据全部置为零,再进行离散Fourier逆变换.“+”为原始数据,“o”为置零后变换得到的数据,与${x(k)}$比较几乎重合.
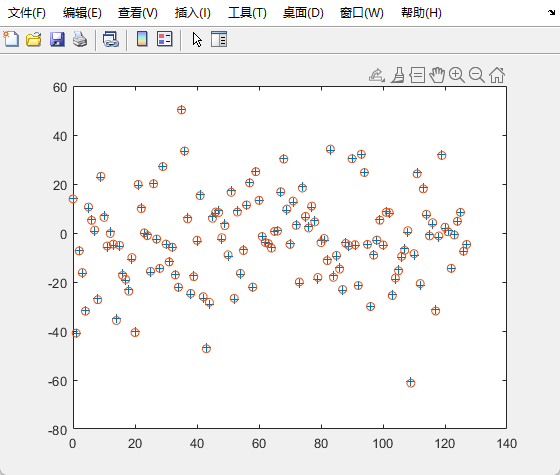
取$\delta_0 = 50$,同样处理后得到的数据,与${x(k)}$比较有些小误差.
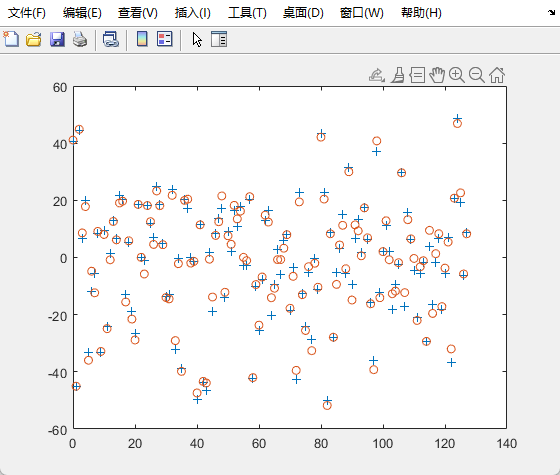
取$\delta_0 = 100$,同样处理后得到的数据,与${x(k)}$比较误差清晰可见,但不是很大.
- 对于N=32,64,128,
(1) 产生两个实数序列${x(k)}{k=0}^{N-1}$和${y(k)}{k=0}^{N-1}$;
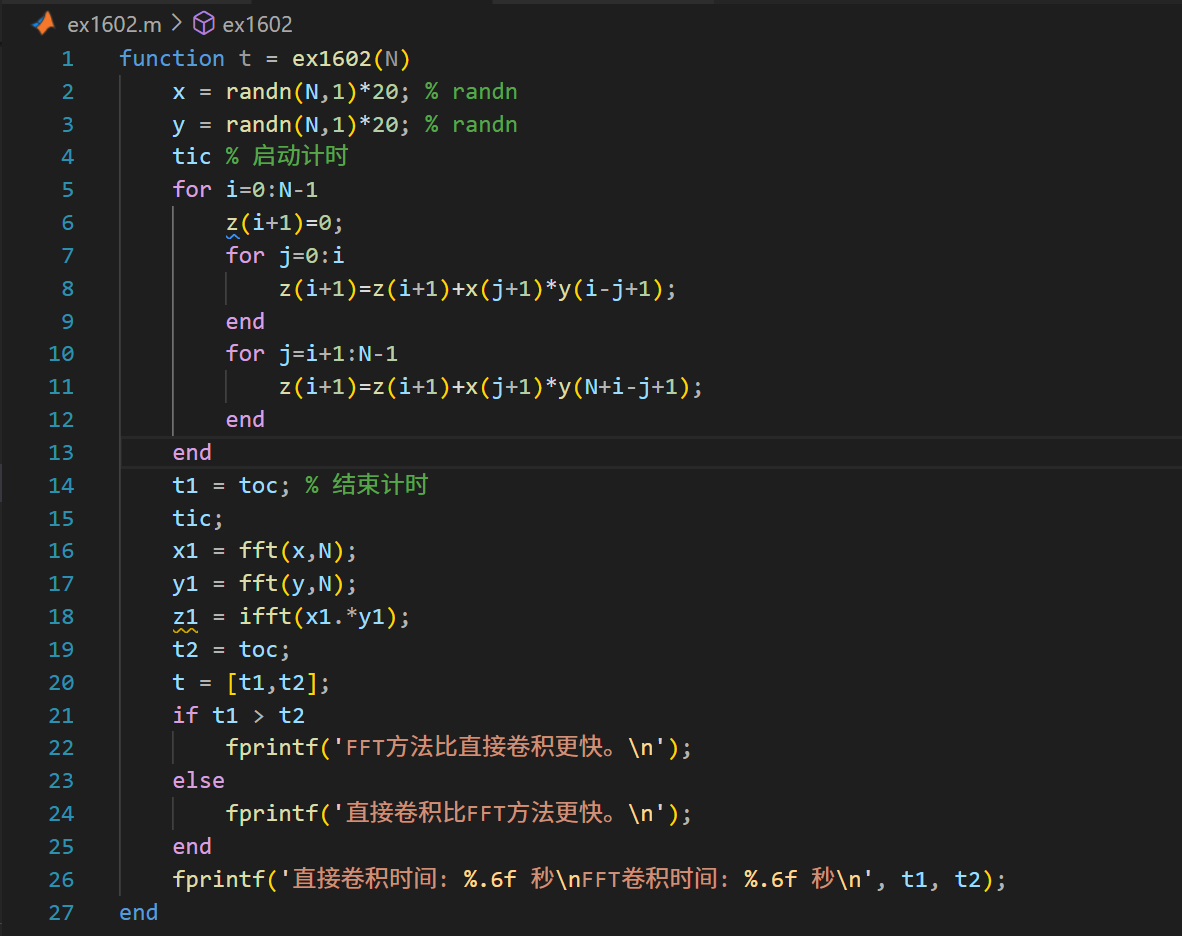
(2) 用直接方法计算${x(k)}$和${y(k)}$的卷积${z(k)}_{k=0}^{N-1}$;
(3) 改用离散Fourier变换的**,用FFT计算${z(k)}$;
(4) 结合N比较两种算法所用的时间.
- 利用FFT计算多项式$\sum_{n=0}^{m}{\frac{(-1)^nx^{2n+1}}{(2n+1)!}}$和$\sum_{n=0}^{m}{\frac{(-1)^nx^{2n}}{2n!}}$的乘积,并与$\frac{\sin2x}{2}$的Taylor级数的相应项比较.
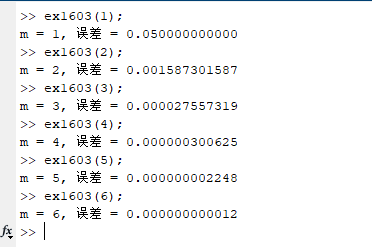
解: 源程序为ex1603.m 运行结果如下
随着m的增加,误差迅速减小。
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)