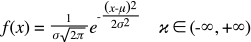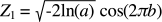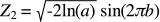正态分布 — 更真实地还原动画
JChehe opened this issue · 0 comments
在某些场景中,正态分布比随机分布更能还原自然现象。本文将阐述正态分布的相关知识,并结合案例讲解如何在动画中使用正态分布。
什么是正态分布
其实,大家都熟知随机数,通过 Math.random() 就能返回一个 [0, 1) 区间内的 伪随机数。例如:当抛硬币的次数足够大时,正/反面的出现概率均为 50%。对于这种均匀随机数的情况是可以通过 Math.random() 模拟实现的。然而,自然界中有很多变量是服从或近似服从正态分布的。
正态分布是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
一般地,如果对于任何实数 a, b(a < b),随机变量 X 满足:
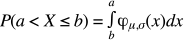
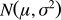
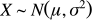
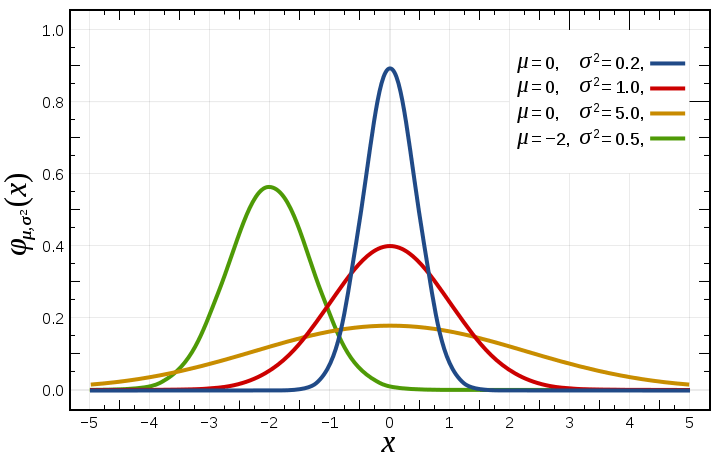
正态分布的函数表达式:
当期望值 μ 为 0(即正态曲线关于 Y 轴对称),标准差 σ 为 1 时,则为标准正态分布,记作 N(0, 1)。
因为正态分布完全由 μ 和 σ 确定,所以可以通过研究 μ 和 σ 对正态曲线的影响来认识正态曲线的特点。
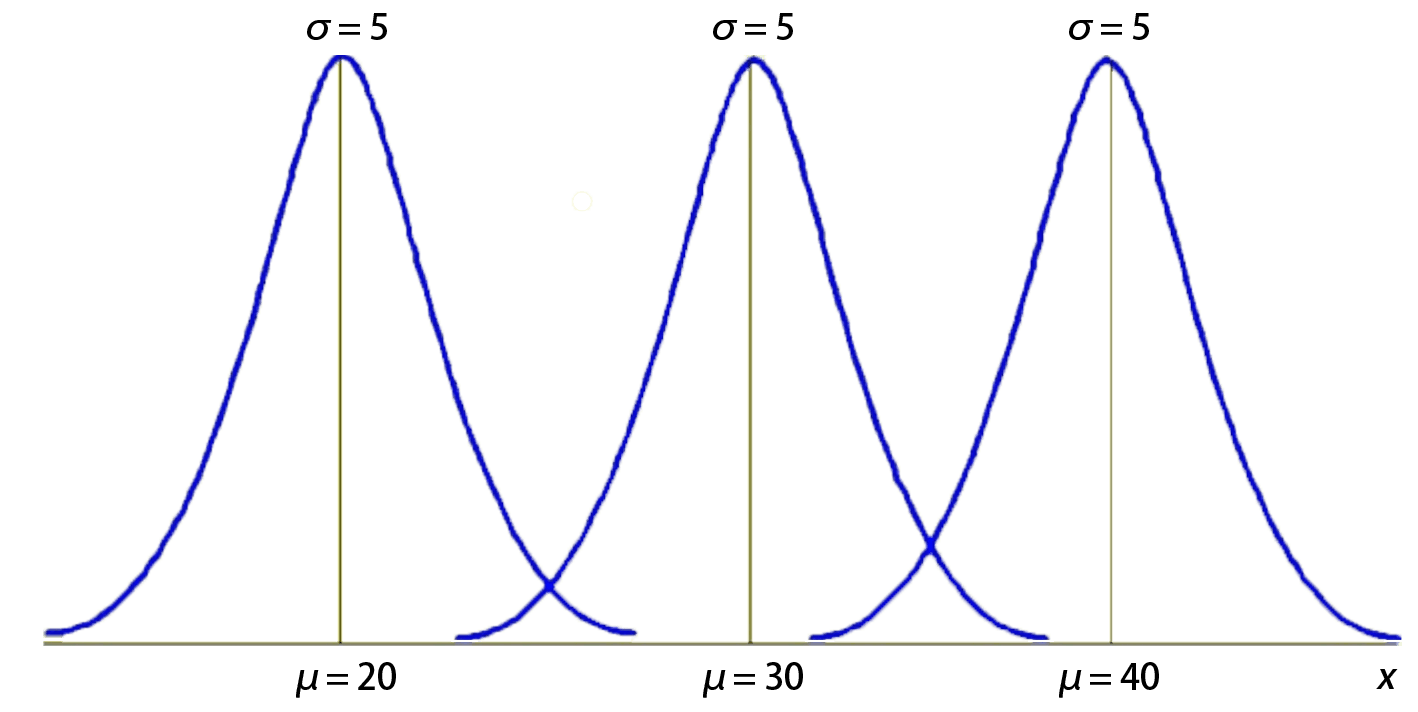
(1)先确定 σ 值,μ 取不同值的图像如下:
当 σ 一定时,曲线随着 μ 的变化而沿 x 轴平移。
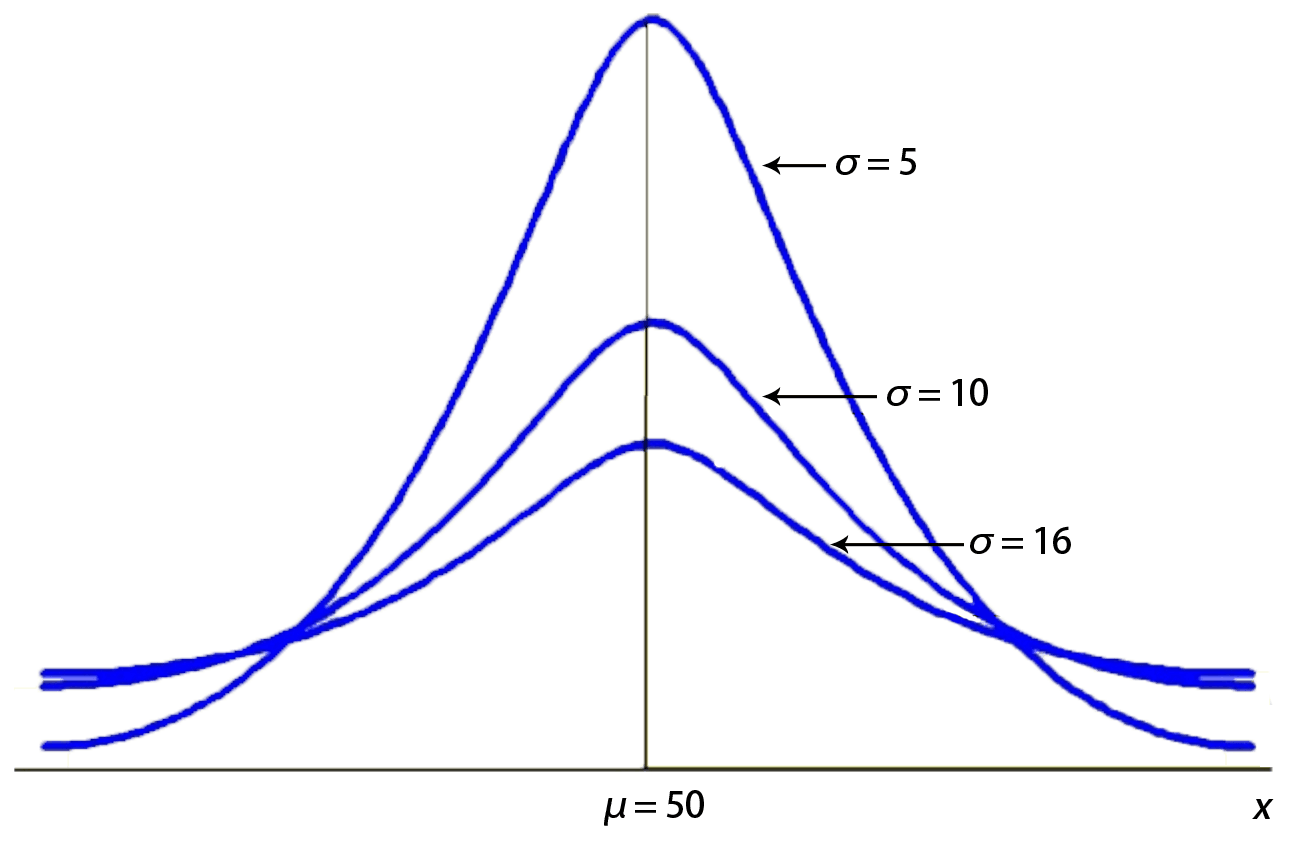
(2)再固定 μ 值,σ 取不同值的图像如下:
当 μ 一定时,曲线的形状由 σ 决定。σ 越少,曲线越“瘦高”,表示总体的分布越集中;σ 越大,曲线越“矮胖”,表示总体的分布越分散。
关于正态分布的基础知识,本文介绍至此。更多知识和实际应用的资料,读者可自行搜索。
前人栽树,后人乘凉
显然,想要在程序中实现期望值为 μ、标准差为 σ 的正态分布并不是件容易的事。ECMAScript 目前也没有提供一个直接生成服从正态分布的随机数的函数。但已有前人给出了实现算法,其中 Box-Muller transform 算法是一个能根据均匀分布的随机数来产生服从正态分布的随机数算法。
当然,也有其他生成服从正态分布随机数的算法:
- Central limit theorem
- Inverse transform sampling
- Marsaglia polar method
- Ziggurat algorithm
- ...
因为 Box-Muller transform 算法效率较高,并且计算过程比较简单,在很长时间内都是生成服从正态分布随机数的“标准”算法,所以本文就结合此算法进行阐述。
Box-Muller
根据 Box-Muller 算法,假设 a、b 是两个服从均匀分布并且取值范围在 [0, 1] 的随机数,我们就可以通过下面的公式得到两个满足标准正态分布(均数 μ 为 0,标准差 σ 为 1)的随机数 Z1 和 Z2。
得到的 Z1 和 Z2 是独立的、服从标准正态分布的随机数。因此,读者只要将 Z1 和 Z2 作为两个没有任何关联的随机数去使用即可。
实际案例
下面看看“撒金币”分别在均匀随机和正态分布下的表现,看看哪个更能俘获你的心。
See the Pen 均匀分布的随机数 by Jc (@JChehe) on CodePen.
<script async src="https://static.codepen.io/assets/embed/ei.js"></script>See the Pen 服从正态分布的随机数 by Jc (@JChehe) on CodePen.
<script async src="https://static.codepen.io/assets/embed/ei.js"></script>“撒金币”案例主要对每个金币的水平速度 vx 和垂直速度 vy 应用独立的随机数。
对于均匀分布的随机数,我们直接使用 Math.random() 实现。而对于服从正态分布的随机数,则通过 Box-Muller 算法,其大概过程如下:
// 因为 Math.random() 返回 [0, 1),1 - Math.random() 得到 (0, 1],避免出现 ln(0) = -infinite
const rand = 1 - Math.random()
const randR = Math.sqrt(-2 * Math.log(rand))
const randT = 2 * Math.PI * Math.random()
Z1 = randR * Math.cos(randT)
Z2 = randR * Math.sin(randT)结语
对于“撒金币”案例,正态分布是否比随机分布更好,也许见仁见智。但使用正确的方式还原自然现象,无疑能给用户带来更真实的体验。