Phase correction struggles with crossing echoes

[HKaras]

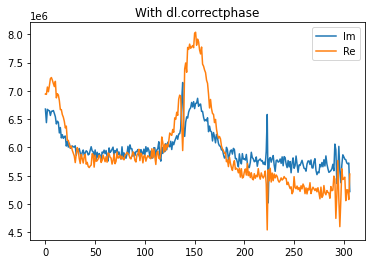
In DEER traces with a significant crossing echoes, the correctphase function sometimes fails to find the correct phase value and can even make the phase worse.

Here is an example:
Note: The imaginary part has been shifted in the yaxis to make it clearer.

As can be seen here the phase gets worse.correctphase get a phase of 0.19 however, data is correctable using a phase of -0.2 as can be seen below:

Here is the data:
phasecorrection_with_crossing_echoes.zip

[luisfabib]

After some analysis I noticed that phase correction is not failing due to the crossing echoes, but due to the fact that there appears to be an imaginary offset contribution. This means that the best phase correction would results in an imaginary contribution that has a non-zero mean. The current implementation in correctphase assumes that the imaginary component has zero mean.

PR #395 implements a new option offset that allows the function to account for that offset in the optimization of the phase, resulting in the correct behavior:

import deerlab as dl 
import matplotlib.pyplot as plt 
import numpy as np 
file = "D:\lufa\projects\DeerLab\Issues\#392\(autodeer)_(BenchB)_(DEER_5P_Q)_2hrs.DSC"

t,Vexp = dl.deerload(file)


plt.figure(figsize=[15,4])

plt.subplot(131)
plt.plot(t,Vexp.real,'b',label='real')
plt.plot(t,Vexp.imag,'r',label='imag')
plt.title(f'Raw data')
plt.legend(loc='best')


Vre,Vim,phase = dl.correctphase(Vexp,full_output=True)

plt.subplot(132)
plt.plot(t,Vre,'b',label='real')
plt.plot(t,Vim,'r',label='imag')
plt.title(f'Old (default) behavior \n offset=False  -> phase={phase[0]:.2f}rad')
plt.legend(loc='best')

Vre,Vim,phase = dl.correctphase(Vexp,full_output=True,offset=True)

plt.subplot(133)
plt.plot(t,Vre,'b',label='real')
plt.plot(t,Vim,'r',label='imag')
plt.title(f'New (optional) behavior \n offset=True  -> phase={phase[0]:.2f}rad')
plt.legend(loc='best')
plt.show()

[HKaras]

Many thanks, that looks much better. Now I just need to identify the cause of my imaginary offset.😢