clarification on norm loss calculation; possible bug?

[rllin]

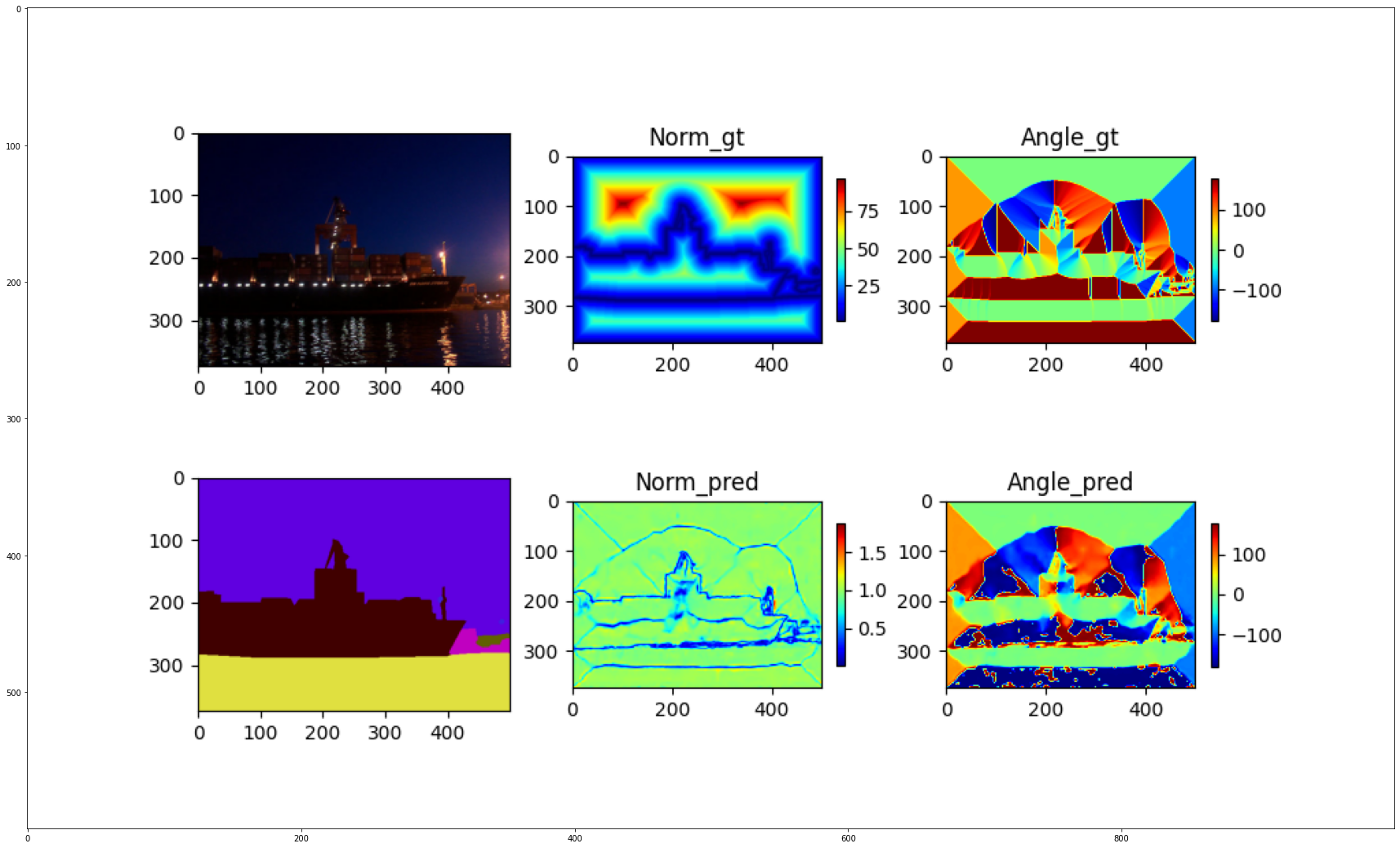
when i look at the image at https://github.com/JianqiangWan/Super-BPD/blob/master/post_process/2009_004607.png

shown here

the norm_pred seems to decrease to blue (< 0.5) in the center of the cat's face (farther from the boundary). this also happen for all midpoints from the boundary of the cat. this is extremely different than the norm_gt

when I look at the code in

https://github.com/JianqiangWan/Super-BPD/blob/master/vis_flux.py#L45

that seems like the correct calculation for the norm

I've run this on a few other examples

and a similar thing seems to happen.

this led me to go investigate the implementation of the loss

If I'm understanding the loss as defined in the paper

that means norm_loss should be pred_flux - gt_flux like in https://github.com/JianqiangWan/Super-BPD/blob/master/train.py#L42

norm_loss = weight_matrix * (pred_flux - gt_flux)**2

however, this happens after https://github.com/JianqiangWan/Super-BPD/blob/master/train.py#L39. which, I believe, is incorrect

I believe that L39 needs to happen after L42. otherwise, the norm_loss as-is is actually training the norm values to be angle values.

This makes sense as if we look at the norm_pred outputs, they look more similar to the norm_angle outputs than they should be.

HOWEVER, I could be completely misunderstanding the norm_loss term, so please let me know if I am! 🤞

[JianqiangWan]

Emmm, I am sorry for the confusion of norm gt (It is wrong, norm gt should be 1 at each pixel. Actually, it is a distance transform map). The calculation of gt flux can be seen in sec 3.1 of origin paper, returned gt_flux of datasets.py is not normalized by corresponding distance because the visualization of norm gt will be collapse.

Super-BPD/datasets.py

Lines 97 to 99 in 3c44638

	diff = grid - nearPixel
	direction_field[:, img > 0] = diff[:, img > 0]

So the normalization process is put in the loss calculation function.

[rllin]

thanks for the fast response @JianqiangWan !

however do you understand my concern with the pred_norm collapsing at unexpected places? perhaps I'm misunderstanding pred_norm?

[rllin]

i am also then confused that

Super-BPD/train.py

Lines 39 to 48 in 3c44638

	gt_flux = 0.999999 * gt_flux / (gt_flux.norm(p=2, dim=1) + 1e-9)
	# norm loss
	norm_loss = weight_matrix * (pred_flux - gt_flux)**2
	norm_loss = norm_loss.sum()
	# angle loss
	pred_flux = 0.999999 * pred_flux / (pred_flux.norm(p=2, dim=1) + 1e-9)
	angle_loss = weight_matrix * (torch.acos(torch.sum(pred_flux * gt_flux, dim=1)))**2

gt_flux is normalized (because it was not in datasets.py) for the norm loss

but pred_flux is normalized for the angle loss and not the norm loss

[JianqiangWan]

We define gt flux at each pixel as a two-dimensional unit vector pointing from its nearest boundary to the pixel. So gt flux around medial points have nearly opposite directions. It is difficult for neural networks to learn such sharp changes, and the network is more inclined to get a smooth transition (like from -1 to 1, network tend to output -1 -0.5 0 0.5 1).

For the norm loss, gt flux is a two-dimensional unit vector field, pred flux does not to be normalized.
For the angle loss, normalize pred flux inside or outside of torch.acos is the same.

[rllin]

thanks for the thorough response

let me make sure I understand:

1. gt flux transitions directionality upon hitting the medial points. we can see this difficulty in learning sharp transitions in the difference between angle_gt and angle_pred: the transition from media to the boundary in angle_pred shows a gradient (like you mention -1 -0.5 0 0.5 1). your explanation makes sense to me for the angles and is born out by the actual behavior of the network.
2. however, my primary concern is specifically with the norm component. my understanding is that these are direction agnostic, as seen in norm_gt where we see:

boundary ---- medial point ---- boundary
     0 1 2 3 4 5 6 7 6 5 4 3 2 1 0

however, we do not see that this is the case for norm_pred. the network seems to always predict:

boundary ---- medial point ---- boundary
     0 1 1 1 1 1 1 0 1 1 1 1 1 1 0

[JianqiangWan]

We need two channels (x, y) to express a flux field, gt flux around medial points can be roughly expressed as (x1, y1) and (-x1, -y1) since they have opposite direction.

From -x1 to x1 or -y1 to y1, network hardly gets the sharp transition, tending to get smooth transition.
norm = sqrt( x**2 + y**2), so pred norm between medial points (x to -x) or boundary points (-x to x) is very small, but the angle is still correct (we only use angle information for image segmentation).
Again, norm gt at each pixel is 1, 'norm gt' in the picture is a distance transform map before normalization.