SParry is a shortest path calculating Python tool using some algorithms with CUDA to speedup.
It's developing.
所谓工欲善其事必先利其器。
SParry 是一个最短路径计算工具包,封装了诸如:Dijkstra , Bellman-Ford , Delta-Stepping , Edge-Based 等主流的最短路径算法。它也提供了基于CUDA的并行加速版本,以提高开发效率。
同时 SParry 还封装了自动分图计算方法的 Dijkstra 算法,可有效解决大规模图在 GPU 显存不足无法直接并行计算的问题。
下面是开发实验中通过测试的环境。也可以参阅 requirements.txt. 。
Python Version
python3.6
python3.7
Plantform
Windows
Linux
Requirements
cyaron==0.4.2 networkx==2.5 numpy==1.19.4 pycuda==2019.1.2 pynvml==8.0.4
直接下载文件包,即可在主目录中运行 pretreat.py 中的 read() 函数预处理数据,然后就可以放入 calc() 接口函数。
目前不是发行版本,故不可pip安装,开发结构尚不是很完善。
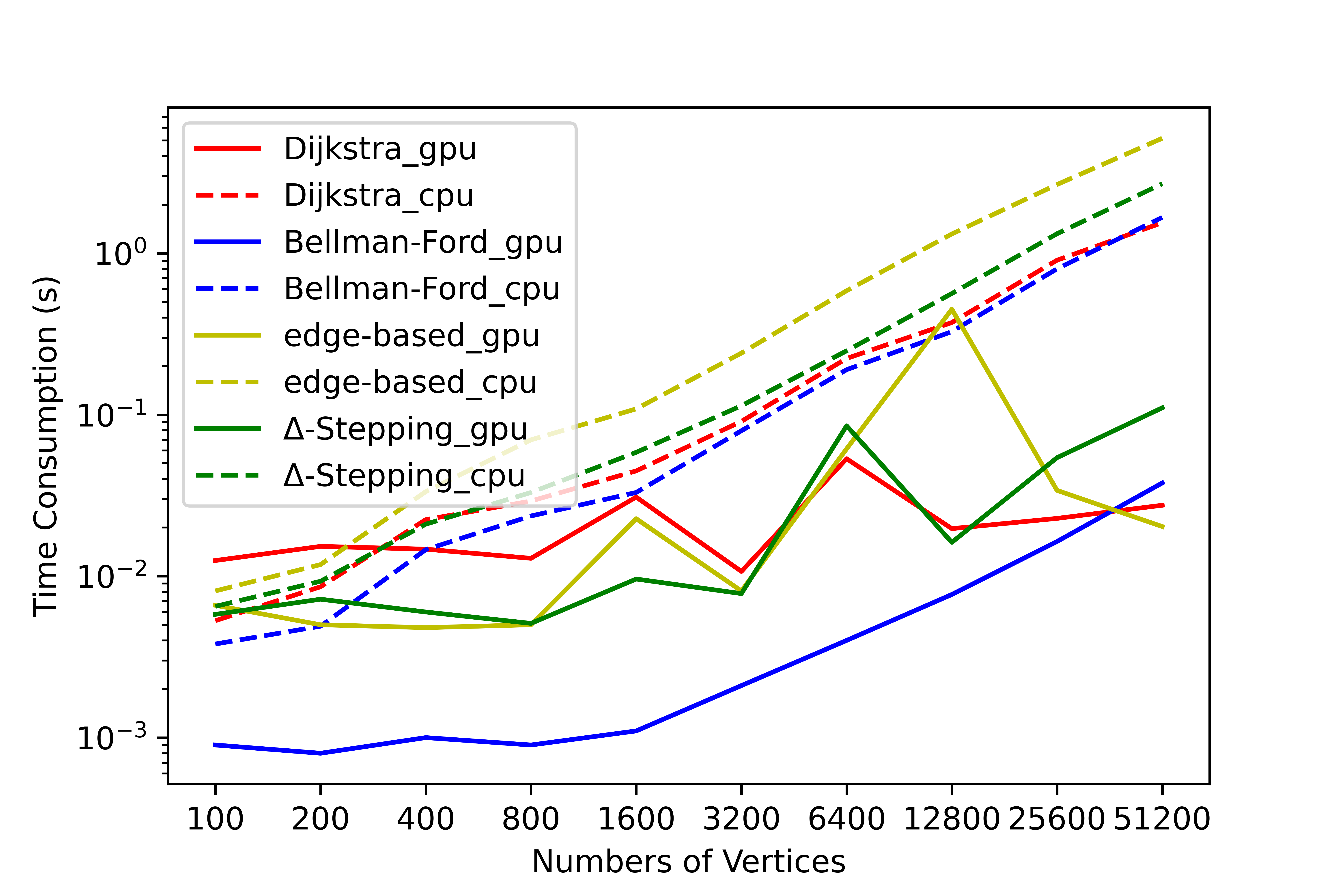
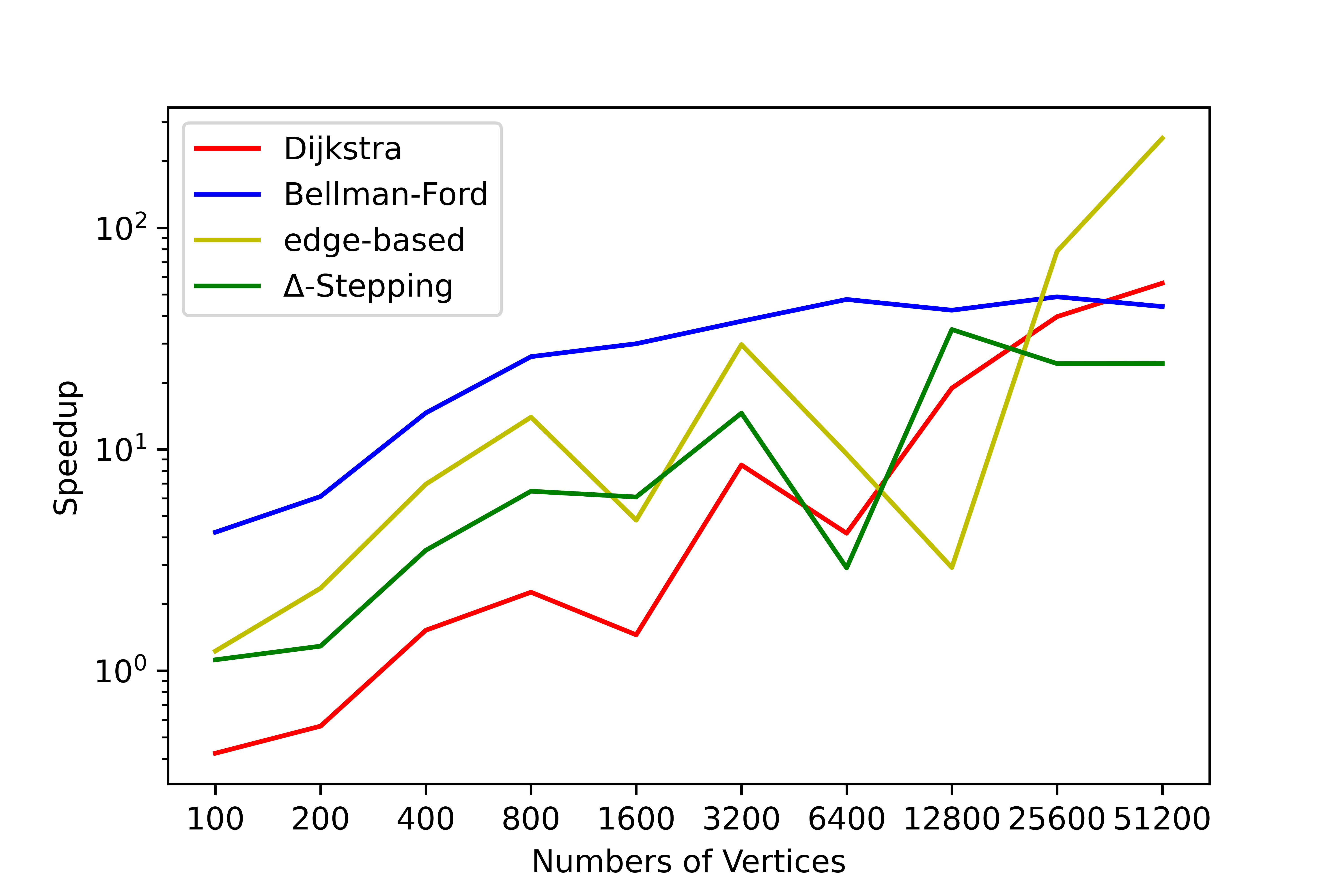
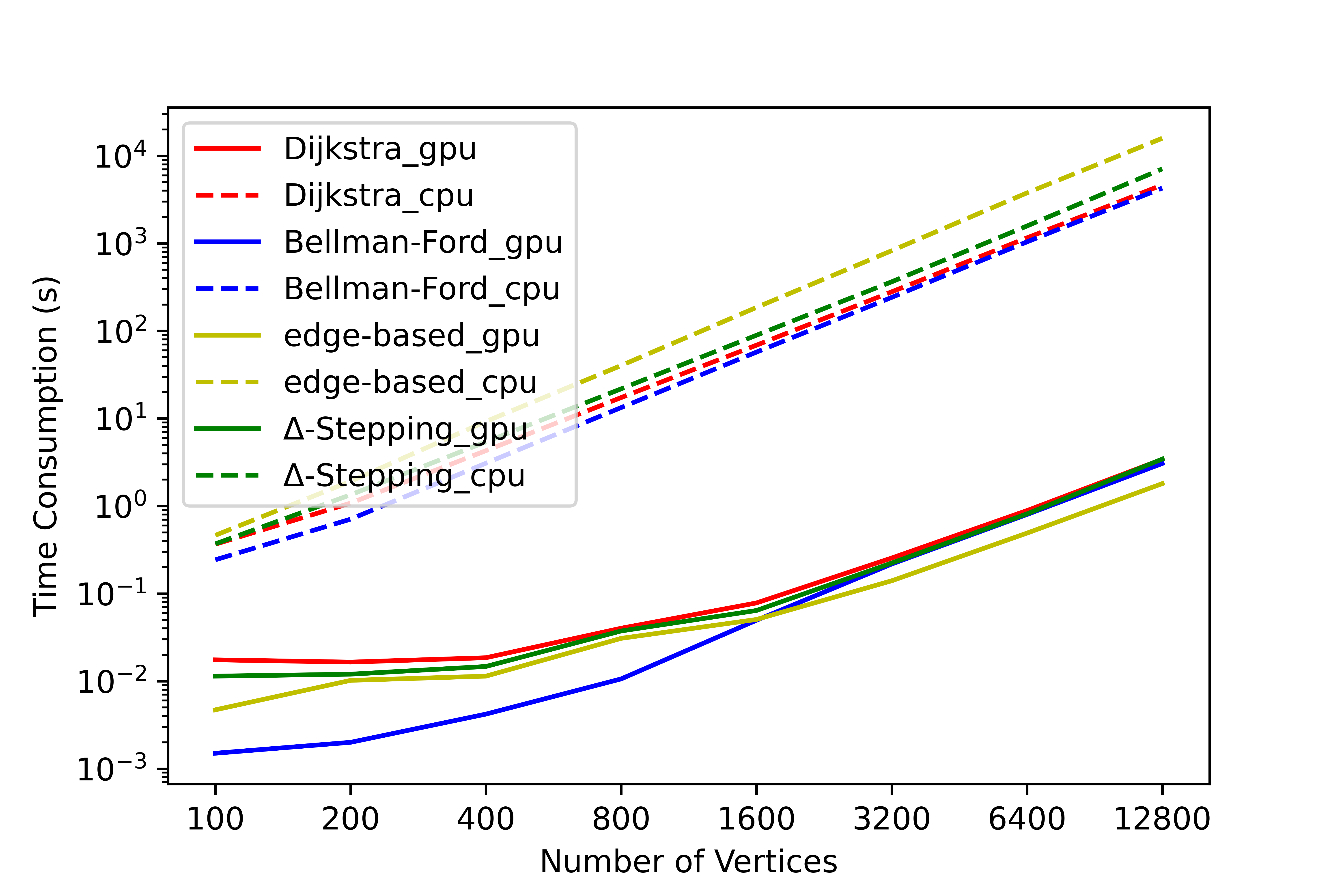
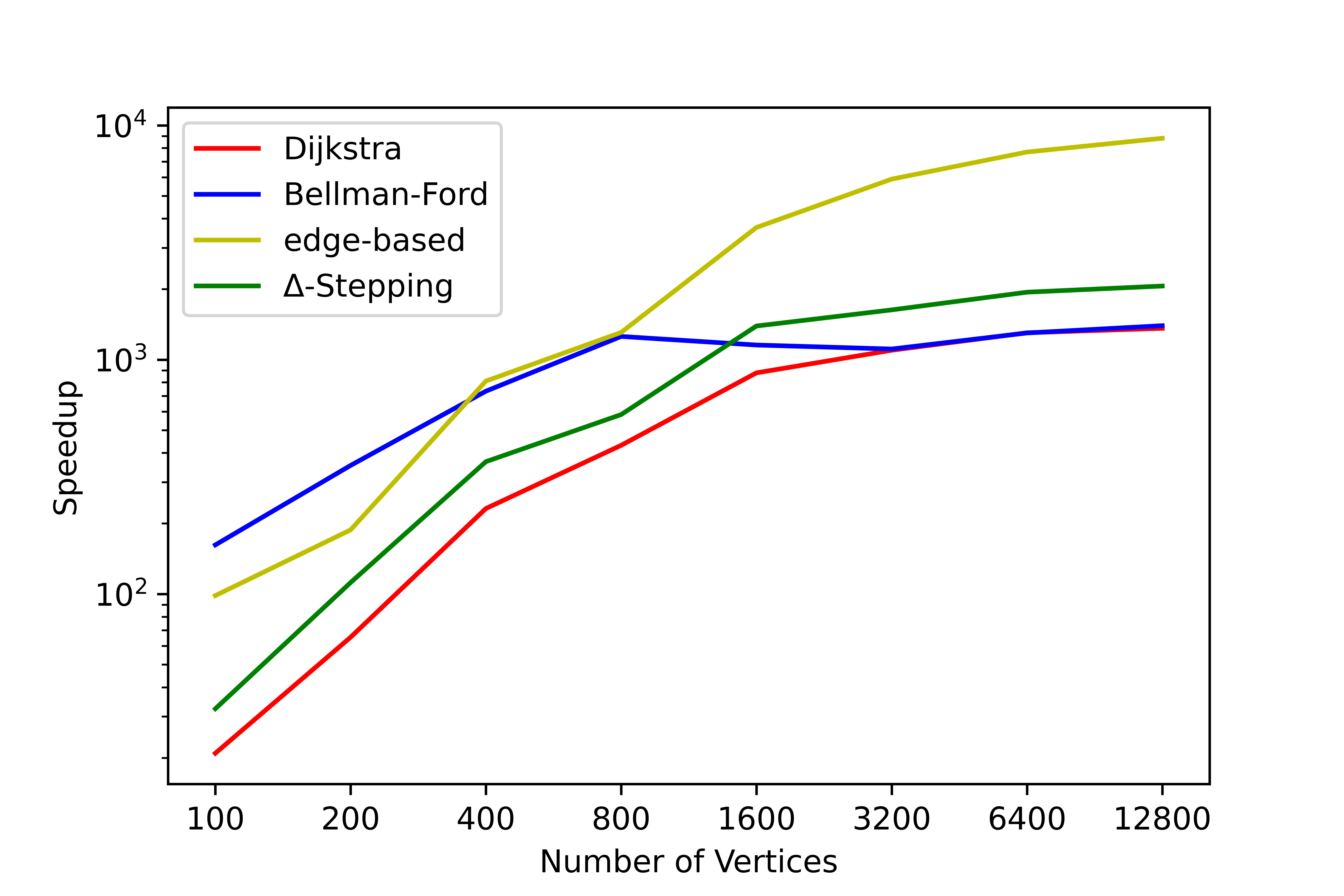
我们对此工具进行了大量的测试,在测试结果中无错误情况发生,统计了各个算法在部分图上计算**单源最短路径问题(SSSP)和全源最短路径问题(APSP)**的用时情况和串并行加速比。下面展示平均度为 4 时,各算法随结点数量变化的用时变化情况,更详细的数据请查阅 SParry/testResult。
SSSP time consumption by degree=4 SSSP speedup ratio by degree=4 APSP time consumption by degree=4 APSP speedup ratio by degree=4本节是帮助 SParry 新手快速上手的简介。同时你也可以查看demo.py。
cd XXX/SParry/当您的图数据在内存中并符合邻接矩阵数据要求 时,可以像下面一样导入您的数据,快速计算结果。
>>> from calc import calc
>>> import numpy as np
>>> from pretreat import read
>>>
>>> matrix = np.array([[0,1,2,3],[1,0,2,3],[2,2,0,4],[3,3,4,0]], dtype = np.int32) # 邻接矩阵的数据
>>> matrix # 模拟已经拥有了一个邻接矩阵的图数据
array([[0, 1, 2, 3],
[1, 0, 2, 3],
[2, 2, 0, 4],
[3, 3, 4, 0]], dtype=int32)
>>>
>>> graph = read(matrix = matrix, # 传入的数据是邻接矩阵
... method = "dij", # 计算方法使用 Dijkstra
... detail = True # 记录图中的详细信息
... ) # 处理图数据
>>> # 计算的最短路径
>>> res = calc(graph = graph, # 传入图数据的类
... useCUDA = True, # 使用 CUDA 加速
... srclist = 0, # 设置源点为 0 号结点
... )
>>>
>>> res.dist # 输出最短路径
array([0, 1, 2, 3], dtype=int32)
>>>
>>> print(res.display()) # 打印相关参数
[+] the number of vertices in the Graph: n = 4,
[+] the number of edges(directed) in the Graph: m = 16,
[+] the max edge weight in the Graph: MAXW = 4,
[+] the min edge weight in the Graph: MINW = 0,
[+] the max out degree in the Graph: degree(0) = 4,
[+] the min out degree in the Graph: degree(0) = 4,
[+] the average out degree of the Graph: avgDegree = 4.0,
[+] the directed of the Graph: directed = Unknown,
[+] the method of the Graph: method = dij.
[+] calc the shortest path timeCost = 0.017 sec
>>>
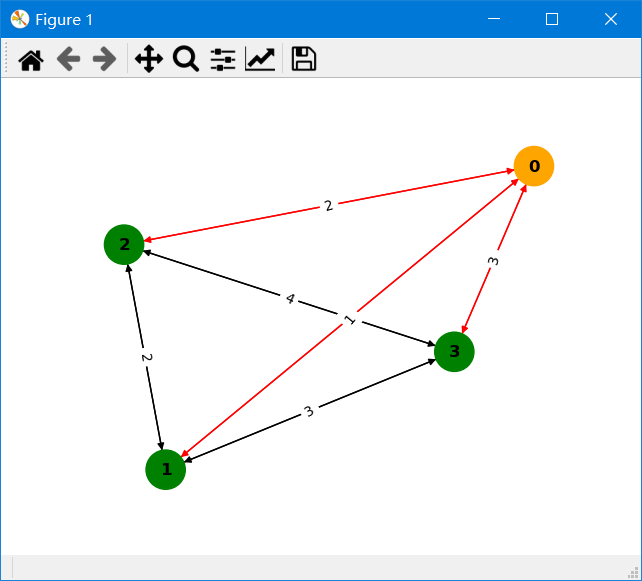
>>> res.drawPath() # 红色的线表示此条边在最短路径上;橙色的点为源点;箭头表示边的方向;边上的数字表示边权。当您的图数据在内存中并符合CSR数据要求 时,可以像下面一样导入您的数据,快速计算结果。
>>> from calc import calc
>>> import numpy as np
>>> from pretreat import read
>>>
>>> CSR = np.array([np.array([0, 2, 3, 4, 4]),
... np.array([1, 2, 3, 1]),
... np.array([1, 3, 4, 5])])
>>> CSR # 模拟已经拥有了CSR格式是图数据
array([array([0, 2, 3, 4, 4]), array([1, 2, 3, 1]), array([1, 3, 4, 5])],
dtype=object)
>>>
>>> graph = read(CSR = CSR, # 传入的数据类型是 CSR
... method = "delta", # 使用的算法为 delta-stepping
... detail = True) # 记录图中的详细信息
>>> # 计算的最短路径
>>> res = calc(graph = graph, # 传入的图数据类
... useCUDA = True, # 使用 CUDA 并行加速
... srclist = 0) # 源点为 0 号结点
>>>
>>> res.dist
array([0, 1, 3, 5], dtype=int32)
>>>
>>> print(res.display()) # 打印相关参数
[+] the number of vertices in the Graph: n = 4,
[+] the number of edges(directed) in the Graph: m = 4,
[+] the max edge weight in the Graph: MAXW = 5,
[+] the min edge weight in the Graph: MINW = 1,
[+] the max out degree in the Graph: degree(0) = 2,
[+] the min out degree in the Graph: degree(3) = 0,
[+] the average out degree of the Graph: avgDegree = 1.0,
[+] the directed of the Graph: directed = Unknown,
[+] the method of the Graph: method = delta.
[+] calc the shortest path timeCost = 0.007 sec当您的图数据在内存中并符合edgeSet数据要求 时,可以像下面一样导入您的数据,快速计算结果。
>>> from calc import calc
>>> import numpy as np
>>> from pretreat import read
>>>
>>> edgeSet = [[0, 0, 2, 1], # 每条边的起始点
... [1, 3, 1, 3], # 每条边的结束点
... [1, 2, 5, 4]] # 每条边的权值
>>>
>>> edgeSet # 模拟已经拥有了edgeSet格式是图数据
[[0, 0, 2, 1], [1, 3, 1, 3], [1, 2, 5, 4]]
>>>
>>> graph = read(edgeSet = edgeSet, # 传入的图数据是 edgeSet
... detail = True) # 需要记录图中的数据
>>> # 计算的最短路径
>>> res = calc(graph = graph, # 传入的图数据类
... useCUDA = False, # 使用 CPU 串行计算
... srclist = 0) # 源点为 0 号结点
>>> res.dist
array([ 0, 1, 2139045759, 2], dtype=int32)
>>>
>>> print(res.display()) # 打印相关参数
[+] the number of vertices in the Graph: n = 4,
[+] the number of edges(directed) in the Graph: m = 4,
[+] the max edge weight in the Graph: MAXW = 5,
[+] the min edge weight in the Graph: MINW = 1,
[+] the max out degree in the Graph: degree(0) = 2,
[+] the min out degree in the Graph: degree(3) = 0,
[+] the average out degree of the Graph: avgDegree = 1.0,
[+] the directed of the Graph: directed = Unknown,
[+] the method of the Graph: method = dij.
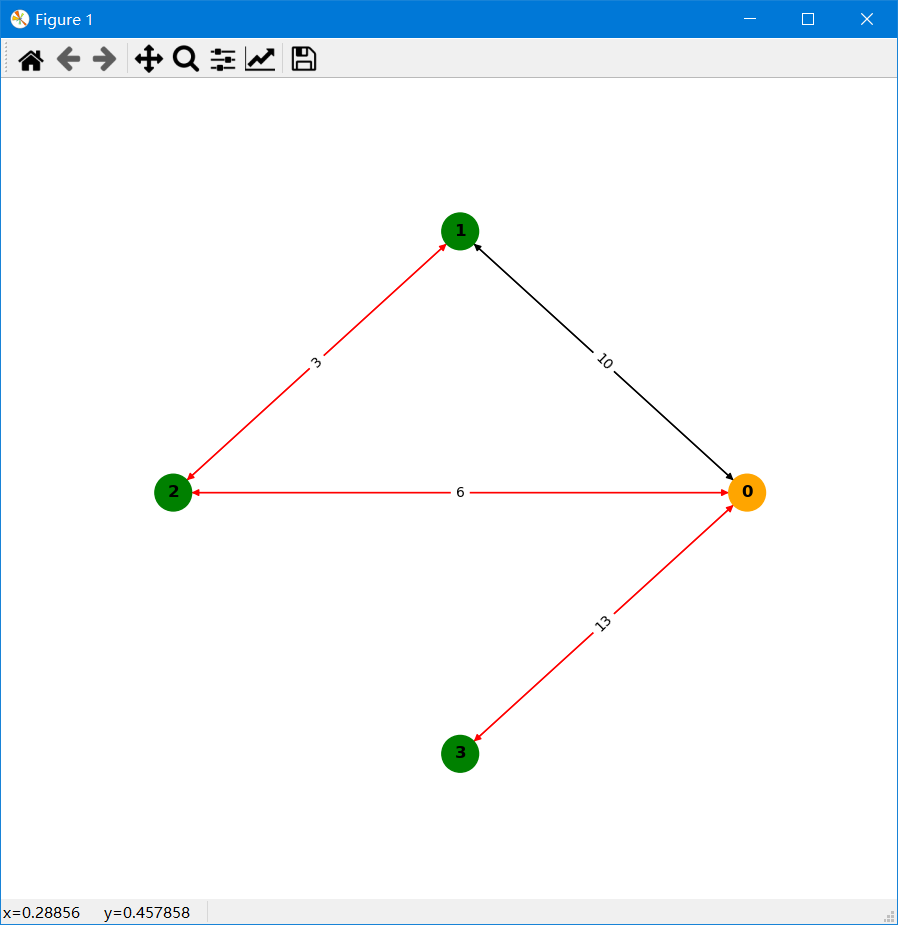
[+] calc the shortest path timeCost = 0.0 sec当您的图数据存储在文件中并符合数据要求时 (文件数据),您也可以传入文件来计算最短路径。
本例子中的文件如下, test.txt 。
4 6
0 1 1
0 2 2
0 3 3
1 2 2
1 3 3
2 3 4
代码如下:
>>> from calc import calc
>>> import numpy as np
>>> from pretreat import read
>>>
>>> filename = "./data/test.txt" # 存储图数据的文件路径
>>> graph = read(filename = filename, # 传入的数据是文件
... method = "spfa", # 使用的算法是 spfa
... detail = True, # 记录图中的细节
... directed = False) # 图为无向图
>>>
>>> res = calc(graph = graph, # 传入的图数据类
... useCUDA = True, # 使用 CUDA 并行加速
... srclist = 0) # 源点为 0 号结点
>>>
>>> res.dist # calculated shortest path
array([0, 1, 2, 3], dtype=int32)
>>>
>>> print(res.display()) # 打印相关参数
[+] the number of vertices in the Graph: n = 4,
[+] the number of edges(directed) in the Graph: m = 12,
[+] the max edge weight in the Graph: MAXW = 4,
[+] the min edge weight in the Graph: MINW = 1,
[+] the max out degree in the Graph: degree(0) = 3,
[+] the min out degree in the Graph: degree(0) = 3,
[+] the average out degree of the Graph: avgDegree = 3.0,
[+] the directed of the Graph: directed = False,
[+] the method of the Graph: method = spfa.
[+] calc the shortest path timeCost = 0.002 sec
>>> res.drawPath() # 红色的线表示此条边在最短路径上;橙色的点为源点;箭头表示边的方向;边上的数字表示边权。关于伪代码请查阅这里 pseudocode。
更多信息请参阅开发者文档。