An application for the foreign exchange market using Bellman-Ford algorithm with the objective of identifying arbitrage opportunities.
Suppose we are individual who want to gain from an arbitrage opportunity. Check this example:
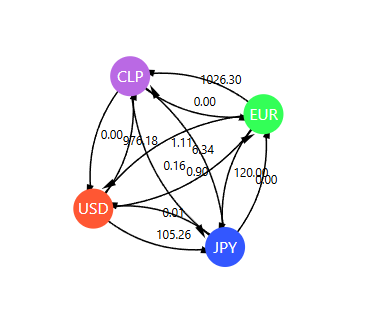
We have 3 differents currencies: USD, EUR and JPY. Between these currencies, there exists exchanges rates, so we want to invest an amount
Imagine these exchange rates:
- 1 USD = 0.9 EUR
- 1 EUR = 120 JPY
- 1 JPY = 0.0092 USD
We can convert these rates to negative logarithms to simplify the mathematics, because it's better to sum than to multiply:
$USD \rightarrow EUR: -log(0.9)$ $EUR \rightarrow JPY: -log(120)$ $JPY \rightarrow USD: -log(0.0092)$
If the sum of all these values is negative, we can execute a sequence of foreign exchange that can generate a net gain. In this case, we can use the Bellman-Ford (BF) algorithm to detect that negative cycle. If the cycle sum is negative, we know that we have an arbitrage opportunity.
Being more explicit with the example:
using logarithms:
With a simple example, if we start with 100 USD:
In the previous example, it's not advantageous to follow this path. But if we change the rates to reflect a market opportunity
A currency is represented as
An arbitrage opportunity exists if:
where:
-
$r_{c_k \rightarrow c_{k+1}}$ is the exchange rate from currency$c_k$ to currency$c_{k+1}$ -
$c_{n+1} = c_1$ to complete the cycle back to the starting currency -
$n$ is the number of exchanges in the cycle.
Alternatively, an arbitrage opportunity exists if:
- We can use
$log(x)$ too.
By assigning weights to the edges of the currency exchange graph as the negative logarithm of the exchange rates:
So, an arbitrage opportunity exists if there is a negative cycle in the graph:
- Trello Activities
- View latex presentation
- This is for the video that i wanna create