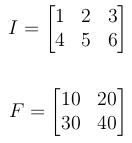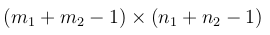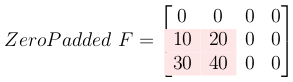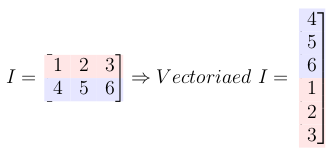Step by step explanation of 2D convolution implemented as matrix multiplication using toeplitz matrices
Instead of using for-loops to perform 2D convolution on images (or any other 2D matrices) we can convert the filter to a Toeplitz matrix and image to a vector and do the convolution just by one matrix multiplication (and of course some post-processing on the result of this multiplication to get the final result)
There are many efficient matrix multiplication algorithms, so using them we can have an efficient implementation of convolution operation.
Mathematical and algorithmic explanation of this process. I will put a naive Python implementation of this algorithm to make it more clear.
Let I be the input signal and F be the filter or kernel.
If the I is m1 x n1 and F is m2 x n2 the size of the output will be:
Zero pad the filter to make it the same size as the output.
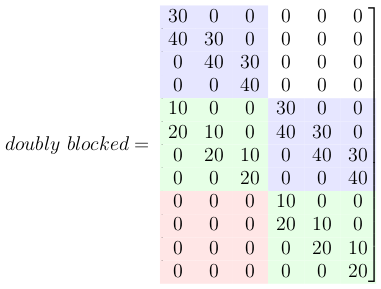
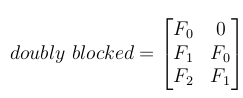
Now all these small Toeplitz matrices should be arranged in a big doubly blocked Toeplitz matrix.
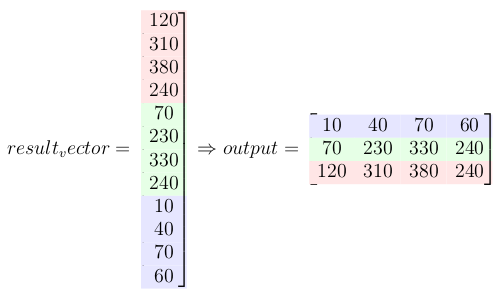
This multiplication gives the convolution result.
See the implementation in python (jupyter notebook)
Look at the notebook
or Look at this pdf in this repo for more details