VaspBandUnfolding: A Python repository from Shibu778

Introduction

VaspBandUnfolding consists of a collection of python scripts that deal with VASP output files.

vaspwfc.py can be used to read the plane-wave coefficients in the WAVECAR file and then generate real-space representation of the pseudo-wavefunction by Fourier transform. Other wavefunction related quantites, e.g. transition dipole moment (pseudo-wavefunction part), inverse participation ratio and electron localization function et al. can also be conveniently obtained.

Moreover, a command line tool named wfcplot in the bin directory can be used to output real-space pseudo-wavefunctions.
paw.py can be used to parse the PAW POTCAR file. A command line tool named potplot in the bin directory can be used to visualize the projector function and partial waves contained in the POTCAR.
aewfc.py can be used to generate all-electron (AE) wavefunction.
unfold.py can be used to perform band unfolding from supercell calculations.

Installation

Requirements
- Numpy
- Scipy
- Matplotlib
- ASE
- pySBT for spherical Bessel transform

Manual Installation

git clone https://github.com/QijingZheng/VaspBandUnfolding
# set the 
cd VaspBandUnfolding
python setup.py install --prefix=/the/path/of/your/dir/
export PYTHONPATH=/the/path/of/your/dir:${PYTHONPATH}

Using Pip

pip install git+https://github.com/QijingZheng/VaspBandUnfolding

Examples

Reading VASP WAVECAR

Pseudo-wavefunction.

As is well known, VASP WAVECAR is a binary file and contains the plane-wave coefficients for the pseudo-wavefunctions. The pseudo-wavefunction in real space can be obtained by 3D Fourier transform on the plane-wave coefficients and represented on a 3D uniform grid which can be subsequently visualized with software such as VESTA.

For a normal WAVECAR, i.e. not gamma-only or non-collinear WAVECAR, one can write a small python script and convert the desired Kohn-Sham states to real space.
```
#/usr/bin/env python
from vaspwfc import vaspwfc

pswfc = vaspwfc('./examples/wfc_r/WAVECAR')
# KS orbital in real space, double the size of the FT grid
phi = pswfc.get_ps_wfc(ikpt=2, iband=27, ngrid=pswfc._ngrid * 2)
# Save the orbital into files. Since the wavefunction consist of complex
# numbers, the real and imaginary part are saved separately.
pswfc.save2vesta(phi, poscar='./examples/wfc_r/POSCAR')
```
- In the above script, pswfc._ngrid is the default 3D grid size and phi is a numpy 3D array of size 2*pswfc._ngrid, with the first dimensiton being x and the last "z".
- The spin, k-point and band index for the KS state are designated by the argumnt ispin, ikpt and iband, respectively, all of which start from 1.
- Generally, the pseudo-wavefunction is complex, pswfc.save2vesta will export both the real and imaginary part of the wavefunction, with the file name "wfc_r.vasp" and "wfc_i.vasp", respectively.
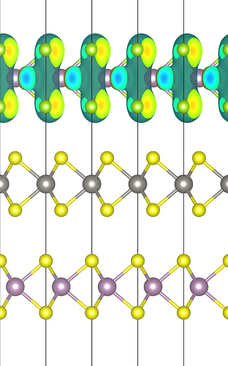
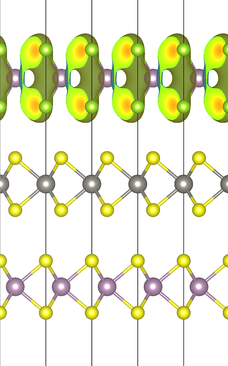
Below are the real (left) and imaginary (right) part of the selected KS orbital:

For gamma-only WAVECAR, one must pass the argument lgamma=True when reading WAVECAR in the vaspwfc method. Moreover, as VASP only stores half of the full plane-wave coefficients for gamma-only WAVECAR and VASP changes the idea about which half to save from version 5.2 to 5.4. An addition argument must be passed.

#/usr/bin/env python
from vaspwfc import vaspwfc

# For VASP <= 5.2.x, check
# which FFT VASP uses by the following command:
#
#     $ grep 'use.* FFT for wave' OUTCAR
#
# Then
#
#     # for parallel FFT, VASP <= 5.2.x
#     pswfc = vaspwfc('WAVECAR', lgamma=True, gamma_half='z')
#
#     # for serial FFT, VASP <= 5.2.x
#     pswfc = vaspwfc('WAVECAR', lgamma=True, gamma_half='x')
#
# For VASP >= 5.4, WAVECAR is written with x-direction half grid regardless of
# parallel or serial FFT.
#
#     # "gamma_half" default to "x" for VASP >= 5.4
#     pswfc = vaspwfc('WAVECAR', lgamma=True, gamma_half='x')

pswfc = vaspwfc('WAVECAR', lgamma=True, gamma_half='x')

For non-collinear WAVECAR, however, one must pass the argument lsorbit=True when reading WAVECAR. Note that in the non-collinear case, the wavefunction now is a two-component spinor.

#/usr/bin/env python
from vaspwfc import vaspwfc

# for WAVECAR from a noncollinear run, the wavefunction at each k-piont/band is
# a two component spinor. Turn on the lsorbit flag when reading WAVECAr.
pswfc = vaspwfc('examples/wfc_r/wavecar_mose2-wse2', lsorbit=True)
phi_spinor = pswfc.get_ps_wfc(1, 1, 36, ngrid=pswfc._ngrid*2)
for ii in range(2):
    phi = phi_spinor[ii]
    prefix = 'spinor_{:02d}'.format(ii)
    pswfc.save2vesta(phi, prefix=prefix,
            poscar='examples/wfc_r/poscar_mose2-wse2')

If only real-space representation of the pseudo-wavefunction is needed, a helping script wfcplot in the bin directory comes to rescue.

$ wfcplot -w WAVECAR -p POSCAR -s spin_index -k kpoint_index -n band_index             # for normal WAVECAR
$ wfcplot -w WAVECAR -p POSCAR -s spin_index -k kpoint_index -n band_index  -lgamma    # for gamma-only WAVECAR
$ wfcplot -w WAVECAR -p POSCAR -s spin_index -k kpoint_index -n band_index  -lsorbit   # for noncollinear WAVECAR

Please refer to wfcplot -h for more information of the usage.

All-electron wavefunction in real space

Refer to this post for detail formulation.

PAW All-Electron Wavefunction in VASP

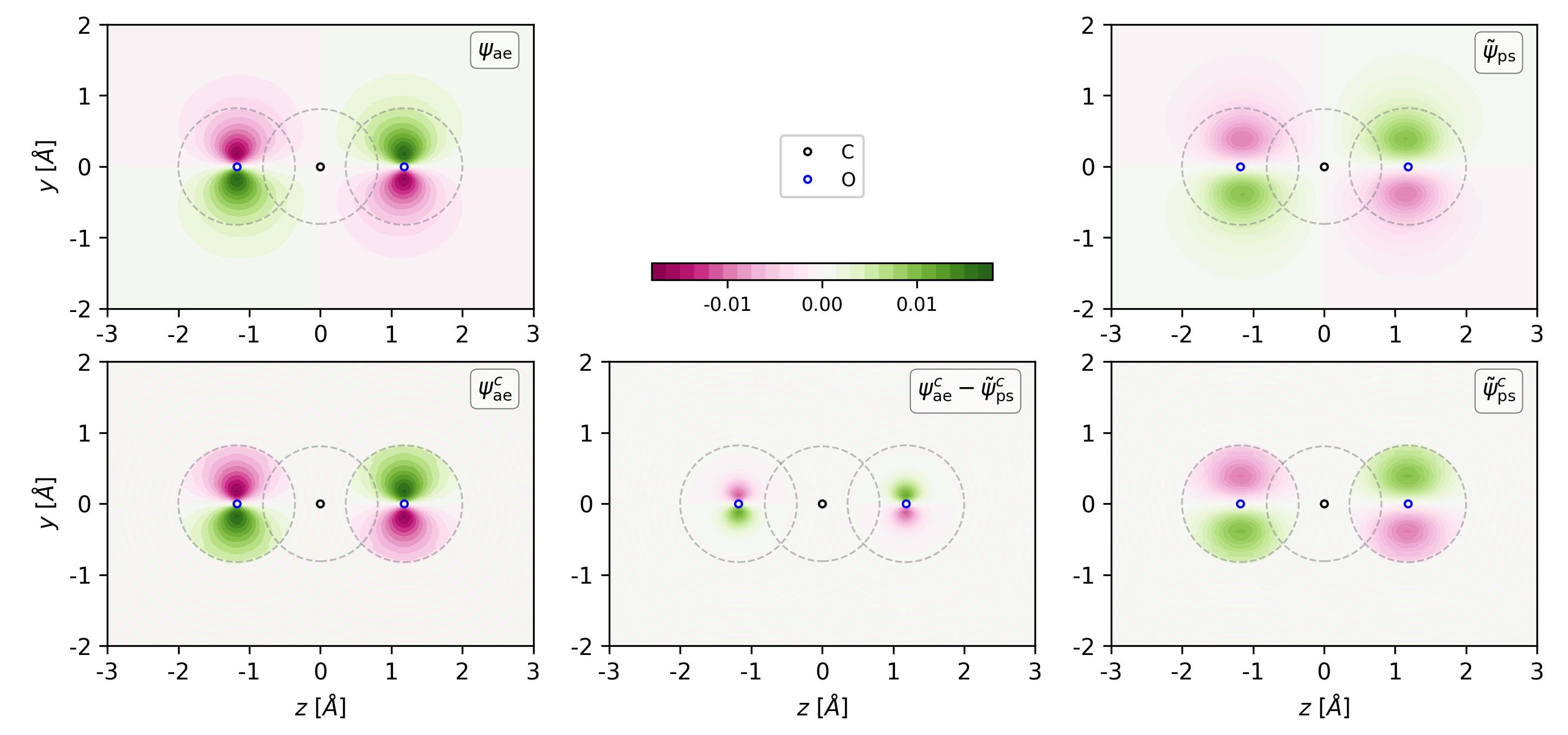
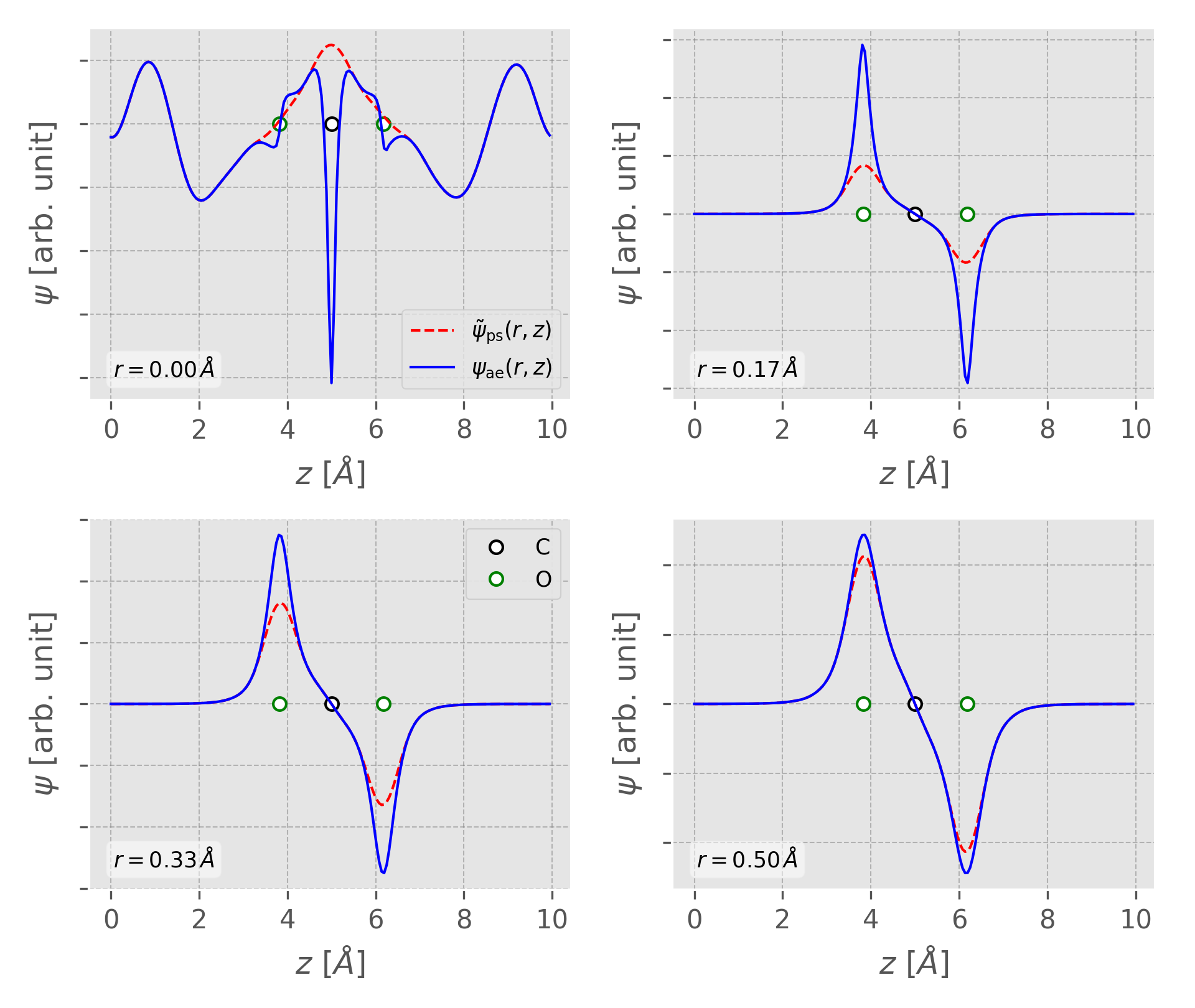
#/usr/bin/env python

from vaspwfc import vaspwfc
from aewfc import vasp_ae_wfc

# the pseudo-wavefunction
ps_wfc = vaspwfc('WAVECAR', lgamma=True)
# the all-electron wavefunction
# here 25x Encut, or 5x grid size is used
ae_wfc = vasp_ae_wfc(ps_wfc, aecut=-25)

phi_ae = ae_wfc.get_ae_wfc(iband=8)

The comparison of All-electron and pseudo wavefunction of CO₂ HOMO can be found in examples/aewfc/co2.

Dipole transition matrix

Refer to this post for detail formulation.

Light-Matter Interaction and Dipole Transition Matrix

Under the electric-dipole approximation (EDA), The dipole transition matrix elements in the length gauge is given by:
```
      <psi_nk | e r | psi_mk>
```
where | psi_nk > is the pseudo-wavefunction. In periodic systems, the position operator "r" is not well-defined. Therefore, we first evaluate the momentum operator matrix in the velocity gauge, i.e.
```
      <psi_nk | p | psi_mk>
```
And then use simple "p-r" relation to apprimate the dipole transition matrix element
```
                                  -i⋅h
    <psi_nk | r | psi_mk> =  -------------- ⋅ <psi_nk | p | psi_mk>
                               m⋅(En - Em)
```
Apparently, the above equaiton is not valid for the case Em == En. In this case, we just set the dipole matrix element to be 0.

NOTE that, the simple "p-r" relation only applies to molecular or finite system, and there might be problem in directly using it for periodic system. Please refer to this paper for more details.

Relation between the interband dipole and momentum matrix elements in semiconductors

The momentum operator matrix in the velocity gauge
```
        <psi_nk | p | psi_mk> = hbar <u_nk | k - i nabla | u_mk>
```
In PAW, the matrix element can be divided into plane-wave parts and one-center parts, i.e.
```
    <u_nk | k - i nabla | u_mk> = <tilde_u_nk | k - i nabla | tilde_u_mk>
                                 - \sum_ij <tilde_u_nk | p_i><p_j | tilde_u_mk>
                                   \times i [
                                     <phi_i | nabla | phi_j>
                                     -
                                     <tilde_phi_i | nabla | tilde_phi_j>
                                   ]
```
where | u_nk > and | tilde_u_nk > are cell-periodic part of the AE/PS wavefunctions, | p_j > is the PAW projector function and | phi_j > and | tilde_phi_j > are PAW AE/PS partial waves.

The nabla operator matrix elements between the pseudo-wavefuncitons
```
    <tilde_u_nk | k - i nabla | tilde_u_mk>

   = \sum_G C_nk(G).conj() * C_mk(G) * [k + G]
```
where C_nk(G) is the plane-wave coefficients for | u_nk >.
```
import numpy as np

from vaspwfc import vaspwfc
from aewfc import vasp_ae_wfc

# the pseudo-wavefunction
ps_wfc = vaspwfc('WAVECAR', lgamma=True)
# the all-electron wavefunction
ae_wfc = vasp_ae_wfc(ps_wfc)

# (ispin, ikpt, iband) for initial and final states
ps_dp_mat = ps_wfc.get_dipole_mat((1,1,1), (1, 1, 9))
ae_dp_mat = ae_wfc.get_dipole_mat((1,1,1), (1, 1, 9))
```
Inverse Participation Ratio

IPR is a measure of the localization of Kohn-Sham states. For a particular KS state \phi_j, it is defined as
```
                \sum_n |\phi_j(n)|^4 
IPR(\phi_j) = -------------------------
              |\sum_n |\phi_j(n)|^2||^2
```
where n iters over the number of grid points.
Electron Localization Function (Still need to be tested!)

In quantum chemistry, the electron localization function (ELF) is a measure of the likelihood of finding an electron in the neighborhood space of a reference electron located at a given point and with the same spin. Physically, this measures the extent of spatial localization of the reference electron and provides a method for the mapping of electron pair probability in multielectronic systems. (from wiki)
- Nature, 371, 683-686 (1994)
- Becke and Edgecombe, J. Chem. Phys., 92, 5397(1990)
- M. Kohout and A. Savin, Int. J. Quantum Chem., 60, 875-882(1996)
- http://www2.cpfs.mpg.de/ELF/index.php?content=06interpr.txt
NOTE that if you are using VESTA to view the resulting ELF file, please rename the output file as "ELFCAR", otherwise there will be some error in the isosurface plot! When VESTA read in CHG*/PARCHG/*.vasp to visualize isosurfaces and sections, data values are divided by volume in the unit of bohr^3. The unit of charge densities input by VESTA is, therefore, bohr^−3. For LOCPOT/ELFCAR files, volume data are kept intact.
```
#/usr/bin/env python
import numpy as np
from vaspwfc import vaspwfc, save2vesta

kptw = [1, 6, 6, 6, 6, 6, 6, 12, 12, 12, 6, 6, 12, 12, 6, 6]

pswfc = vaspwfc('./WAVECAR')
# chi = wfc.elf(kptw=kptw, ngrid=wfc._ngrid * 2)
chi = pswfc.elf(kptw=kptw, ngrid=[20, 20, 150])
save2vesta(chi[0], lreal=True, poscar='POSCAR', prefix='elf')
```
Remember to rename the output file "elf_r.vasp" as "ELFCAR"!

VASP POTCAR

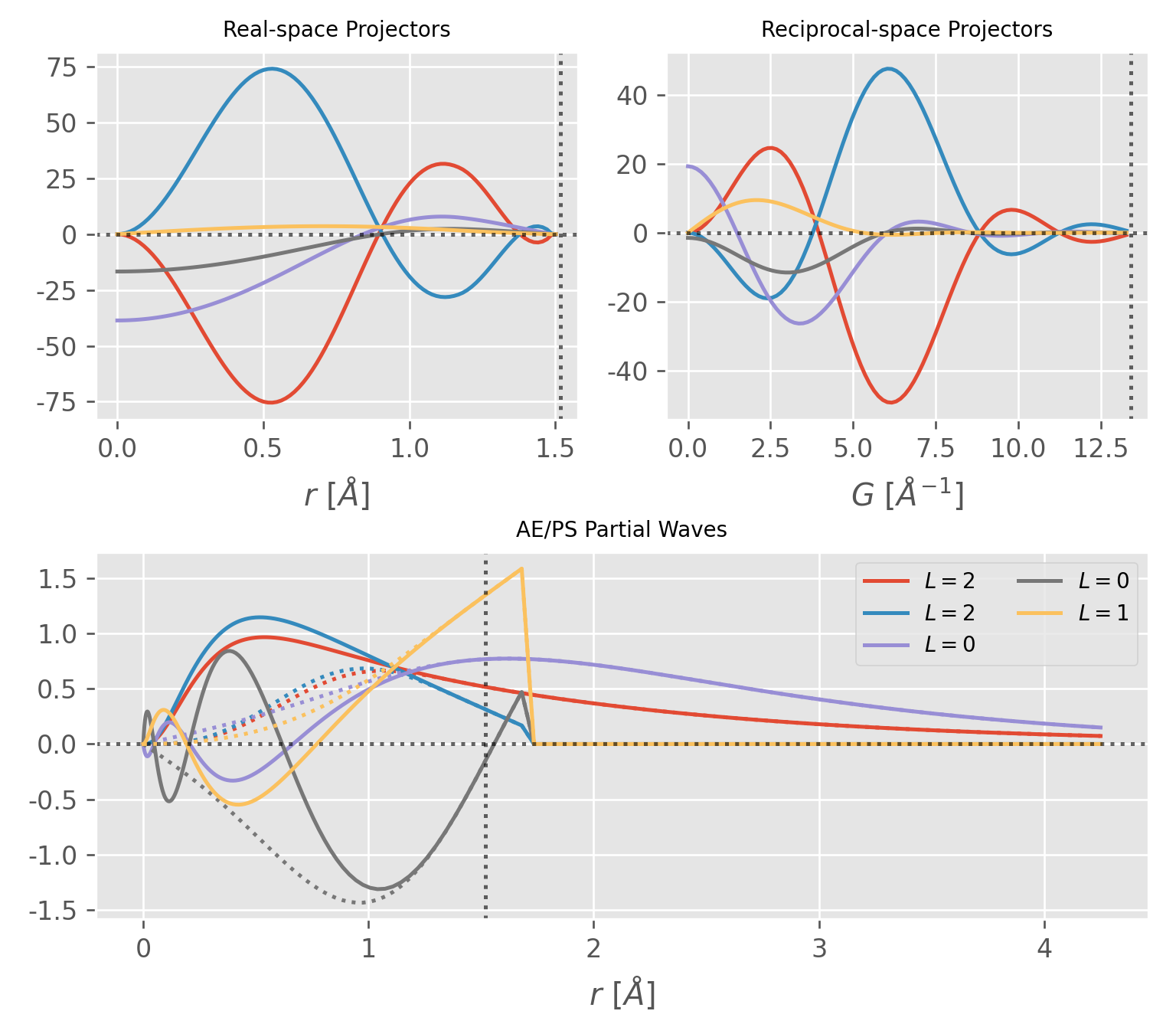
The paw.py contains method to parse the PAW POTCAR (pawpotcar class) can calculate relating quantities in the PAW within augment sphere. For example,

from paw import pawpotcar

pp = pawpotcar(potfile='POTCAR')

# Q_{ij} = < \phi_i^{AE} | \phi_j^{AE} > -
#          < \phi_i^{PS} | \phi_j^{PS} >
Qij = pp.get_Qij()
# nabla_{ij} = < \phi_i^{AE} | nabla_r | \phi_j^{AE} > -
#              < \phi_i^{PS} | nabla_r | \phi_j^{PS} >
Nij = pp.get_nablaij()

A helping script utilizing the paw.py in the bin directory can be used to visulize the projector function and partial waves.

# `Ti` POTCAR for exampleTCAR for example
potplot -p POTCAR

As the name suggests, paw.py also contains the methods (nonlq and nonlr class) to calculate the inner products of the projector function and the pseudo-wavefunction. The related formula can be found in my post.

PAW All-Electron Wavefunction in VASP

Band unfolding

Using the pseudo-wavefunction from supercell calculation, it is possible to perform electronic band structure unfolding to obtain the effective band structure. For more information, please refer to the following article and the GPAW website.

V. Popescu and A. Zunger Extracting E versus k effective band structure from supercell calculations on alloys and impurities Phys. Rev. B 85, 085201 (2012)

Theoretical background with an example can be found in my post:

Band Unfolding Tutorial

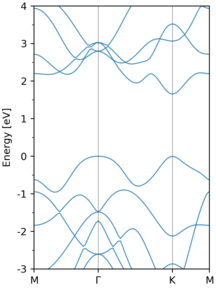
Here, we use MoS₂ as an example to illustrate the procedures of band unfolding. Below is the band structure of MoS2 using a primitive cell. The calculation was performed with VASP and the input files can be found in the examples/unfold/primitive

Create the supercell from the primitive cell, in my case, the supercell is of the size 3x3x1, which means that the transformation matrix between supercell and primitive cell is
```
 # The tranformation matrix between supercell and primitive cell.
 M = [[3.0, 0.0, 0.0],
      [0.0, 3.0, 0.0],
      [0.0, 0.0, 1.0]]
```

In the second step, generate band path in the primitive Brillouin Zone (PBZ) and find the correspondig K points of the supercell BZ (SBZ) onto which they fold.

from unfold import make_kpath, removeDuplicateKpoints, find_K_from_k

# high-symmetry point of a Hexagonal BZ in fractional coordinate
kpts = [[0.0, 0.5, 0.0],            # M
        [0.0, 0.0, 0.0],            # G
        [1./3, 1./3, 0.0],          # K
        [0.0, 0.5, 0.0]]            # M
# create band path from the high-symmetry points, 30 points inbetween each pair
# of high-symmetry points
kpath = make_kpath(kpts, nseg=30)
K_in_sup = []
for kk in kpath:
    kg, g = find_K_from_k(kk, M)
    K_in_sup.append(kg)
# remove the duplicate K-points
reducedK, kid = removeDuplicateKpoints(K_in_sup, return_map=True)

# save to VASP KPOINTS
save2VaspKPOINTS(reducedK)

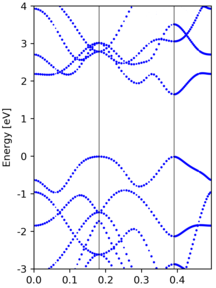
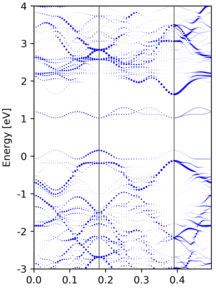
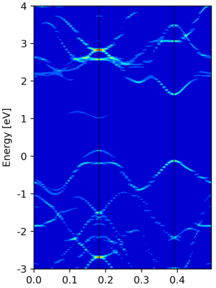
Do one non-SCF calculation of the supercell using the folded K-points and obtain the corresponding pseudo-wavefunction. The input files are in examples/unfold/sup_3x3x1/. The effective band structure (EBS) and then be obtained by processing the WAVECAR file.

from unfold import unfold

# basis vector of the primitive cell
cell = [[ 3.1850, 0.0000000000000000,  0.0],
        [-1.5925, 2.7582909110534373,  0.0],
        [ 0.0000, 0.0000000000000000, 35.0]]

WaveSuper = unfold(M=M, wavecar='WAVECAR')

from unfold import EBS_scatter
sw = WaveSuper.spectral_weight(kpath)
# show the effective band structure with scatter
EBS_scatter(kpath, cell, sw, nseg=30, eref=-4.01,
        ylim=(-3, 4), 
        factor=5)

from unfold import EBS_cmaps
e0, sf = WaveSuper.spectral_function(nedos=4000)
# or show the effective band structure with colormap
EBS_cmaps(kpath, cell, e0, sf, nseg=30, eref=-4.01,
        show=False,
        ylim=(-3, 4))

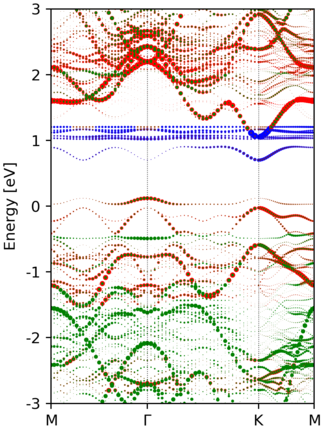
The EBS from a 3x3x1 supercell calculation are shown below:

Another example of EBS from a 3x3x1 supercell calculation, where we introduce a S vacancy in the structure.

Yet another band unfolding example from a tetragonal 3x3x1 supercell calculation, where the transformation matrix is

 M = [[3.0, 0.0, 0.0],
      [3.0, 6.0, 0.0],
      [0.0, 0.0, 1.0]]

Compared to the band structure of the primitive cell, there are some empty states at the top of figure. This is due to a too small value of NBANDS in supercell non-scf calculation, and thus those states are not included.

Band unfolding wth atomic contributions

After band unfolding, we can also superimpose the atomic contribution of each KS states on the spectral weight. Below is the resulting unfolded band structure of Ce-doped bilayer-MoS2. Refer to ./examples/unfold/Ce@BL-MoS2_3x3x1/plt_unf.py for the entire code.

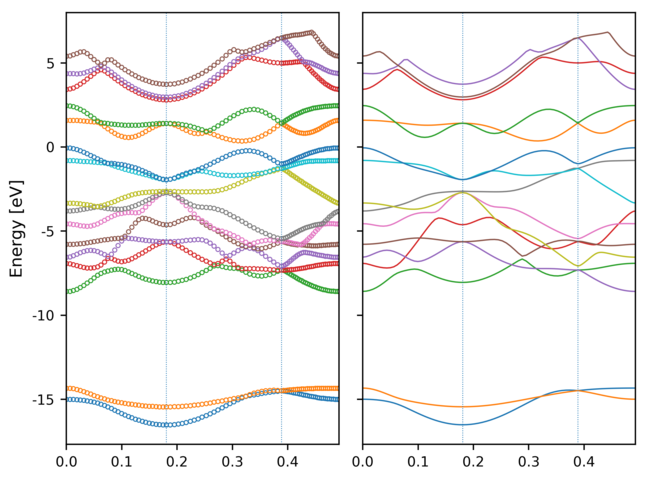
Band re-ordering

Band re-ordering is possible by maximizing the overlap between nerghbouring k-points. The overlap is defined as the inner product of the periodic part of the Bloch wavefunctions.

                    `< u(n, k) | u(m, k-1) >`

Note, however, the WAVECAR only contains the pseudo-wavefunction, and thus the pseudo u(n,k) are used in this function. Moreover, since the number of planewaves for each k-points are different, the inner product is performed in real space.

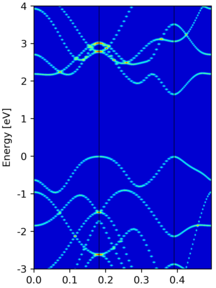
The overlap maximalization procedure is as follows:

Pick out those bands with large overlap (> olap_cut).
Assign those un-picked bands by maximizing the overlap.

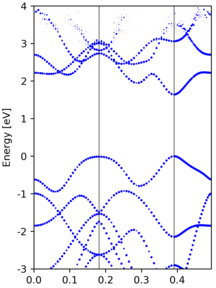
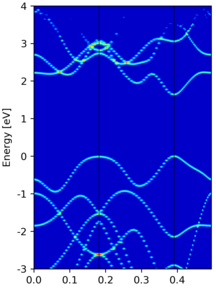
An example band structure re-ordering is performed in MoS2. The result is shown in the following image, where the left/right panel shows the un-ordered/re-ordered band structure.

Shibu778/VaspBandUnfolding