Kolmogorov–Arnold Networks with modified activation (using MLP + positional encoding to represent the activation). The code utilizes torch.vmap to accelerate and simplify the process.
Running the following code for quick experiment:
python experiment.pyfrom kan_layer import KANLayer
model = nn.Sequential(
KANLayer(2, 5),
KANLayer(5, 1)
)
x = torch.randn(16, 2)
y = model(x)
# y.shape = (16, 1)I experimented with a simple objective function:
def target_fn(input):
# f(x,y)=exp(sin(pi * x) + y^2)
if len(input.shape) == 1:
x, y = input
else:
x, y = input[:, 0], input[:, 1]
return torch.exp(torch.sin(torch.pi * x) + y**2)The first experiment set the network as:
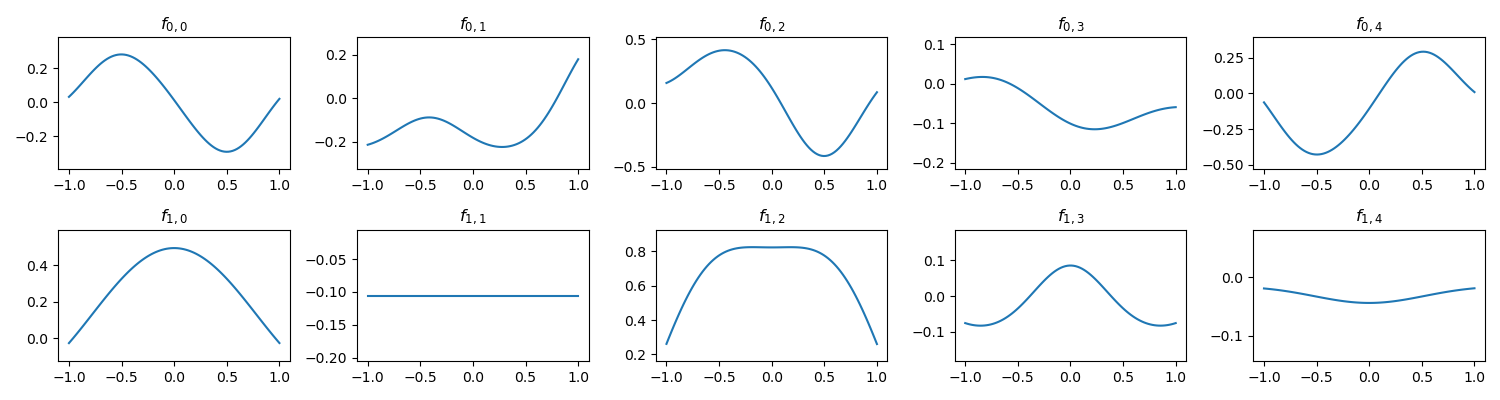
dims = [2, 5, 1]
model = nn.Sequential(
KANLayer(dims[0], dims[1]),
KANLayer(dims[1], dims[2])
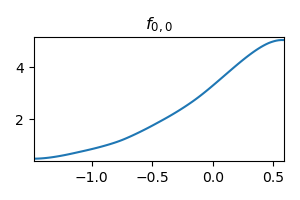
)After training on this, the activation function did learn the
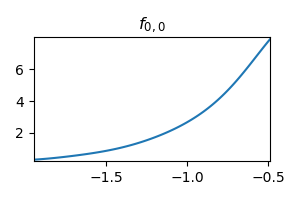
The exponential function is also been learned for the second layer:
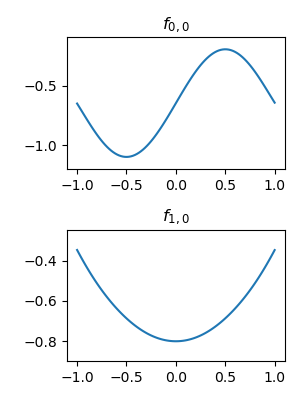
For better interpretability, we can set the network as:
dims = [2, 1, 1]
model = nn.Sequential(
KANLayer(dims[0], dims[1]),
KANLayer(dims[1], dims[2])
)Both the first layer and the second layer learning exactly the target function:
Second layer learning the exponential function:
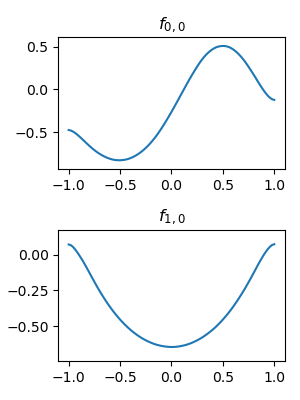
from kan_layer import KANInterpoLayer
model = nn.Sequential(
KANInterpoLayer(2, 5),
KANInterpoLayer(5, 1)
)
x = torch.randn(16, 2)
y = model(x)
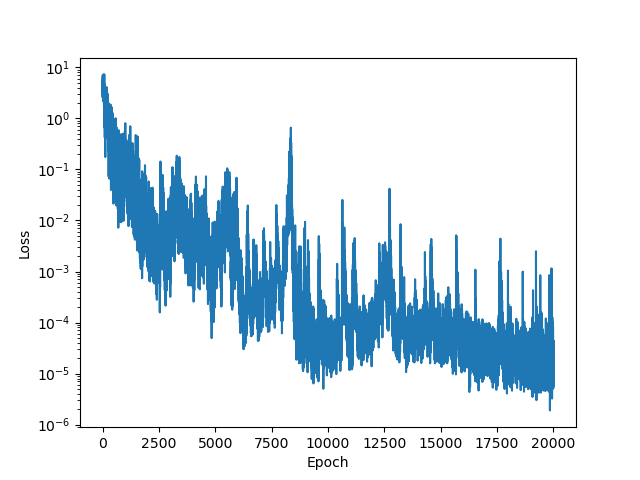
# y.shape = (16, 1)The result shows similar performance. However, this version is harder to train. I guess it is because each parameter only affect the behavior locally, making it harder to cross local minima, or zero-gradient points. Adding smooth_penalty may help.