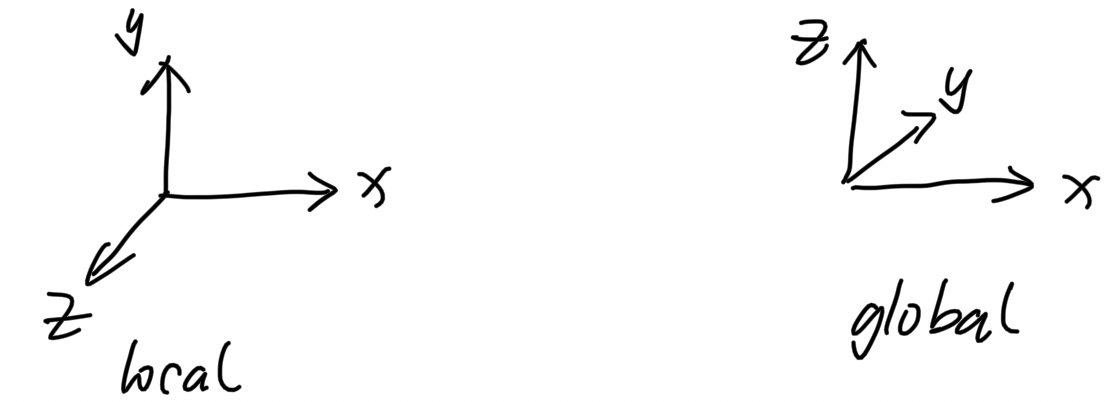一个基于 Path Tracing 的光线追踪渲染器。
- 使用了基于光源面积的采样
- 实现了 Lambert 着色(后续会引入 Phong 着色以及微表面模型)
- 导出必要的光线信息,支持可视化地对每一根光线 debug
参数:400px,256spp
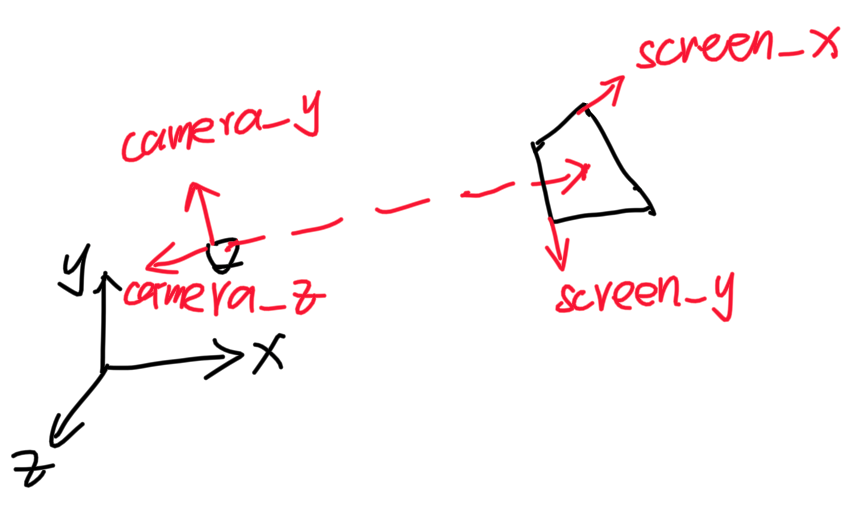
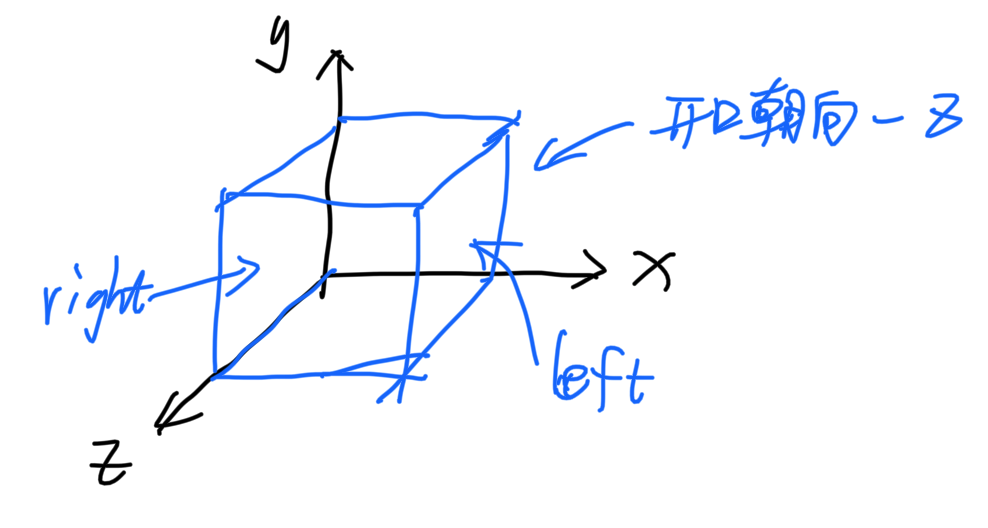
这里有三个坐标系:世界坐标系,摄像机坐标系,屏幕坐标系。
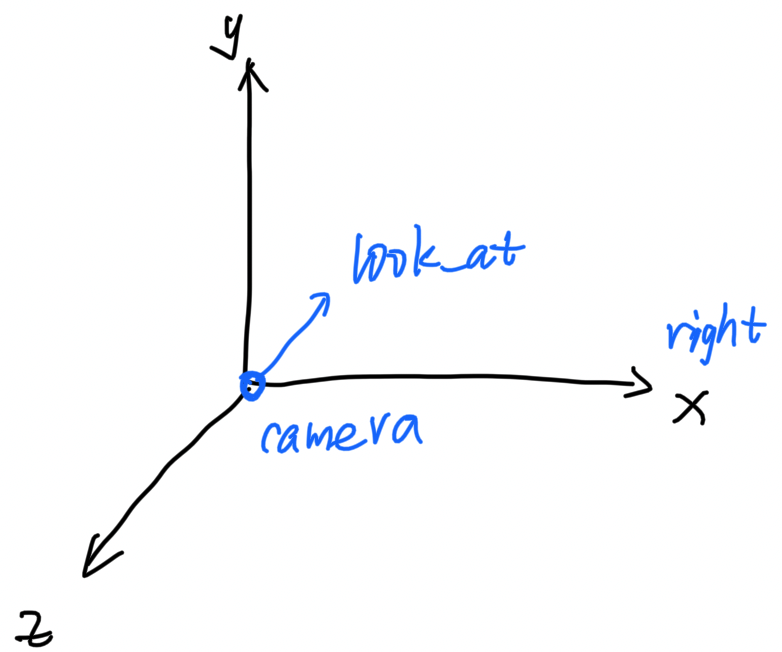
摄像机坐标系固定在摄像机上,-z 为摄像机的朝向,不考虑摄像机的桶滚运动,+x 为摄像机的右方向:
摄像机坐标系的基向量可以表示为:
coor_camera_z = -look_at;
coor_camera_x = cross(vec3(0, 1, 0), coor_camera_z);
coor_camera_y = cross(coor_camera_z, coor_camera_x);从摄像机坐标系变换到世界坐标系:(其中 i, j, k 表示摄像机坐标系的基向量,e 表示摄像机在世界坐标系的位置)
$$
Pos_{world} =
\left[\begin{array}{ccc}
i_x && j_x && k_x && e_x \
i_y && j_y && k_y && e_y \
i_z && j_z && k_z && e_z \
0 && 0 && 0 && 1
\end{array}\right]
\cdot {Pos}_{camera}
$$
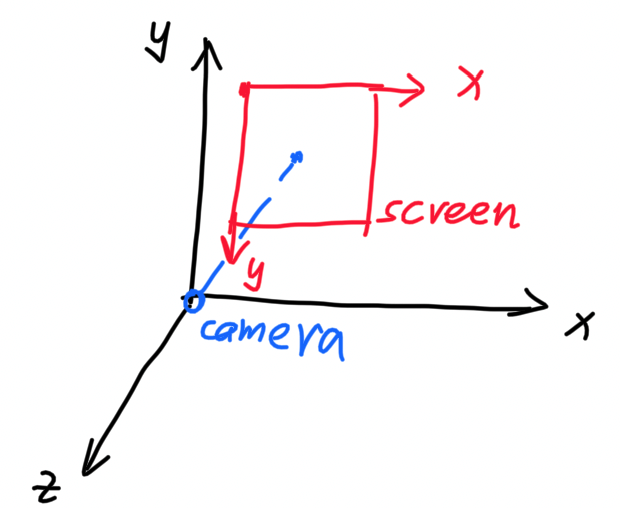
屏幕坐标系位于摄像机坐标系中。
一般来说,摄像机正对着屏幕,距屏幕一定的距离:
屏幕坐标系中的一个像素点 (x_screen, y_screen) 如何转化为摄像机坐标系中的坐标 (x_view, y_view)
需要定义以下参数:
- 摄像机到屏幕的距离:
dis - 摄像机的视场角:
fov - 屏幕的宽高比:
aspect - 屏幕的像素:
screen_h(可以计算出screen_w)
可以计算出,投影平面的宽和高:
view_h = 2 * tan(fov / 2) * dis;
view_w = height * aspect;屏幕坐标和投影平面坐标的对应关系:
屏幕中像素的坐标值 投影平面的坐标值
x: [0 , screen_w] -> [-view_w / 2, view_w / 2]
y: [screen_h, 0 ] -> [-view_h / 2, view_h / 2]
z: -> -1
变换公式为:(考虑到像素中心点在每个像素的**,所以这里使用 0.5 ) $$ x_{view} = (\frac{x_{screen}}{W_{screen}} - 0.5) * \frac{W_{view}}{2} \ y_{view} = (0.5 - \frac{y_{screen}}{H_{screen}}) * \frac{H_{view}}{2} $$
将物体导入后,其 local 坐标系和 global 坐标系的对应图:
这个应用中使用的 cornell-box,其位姿为(local 坐标系):
为了实现 debug 功能,需要将所有的光路信息都记录下来。
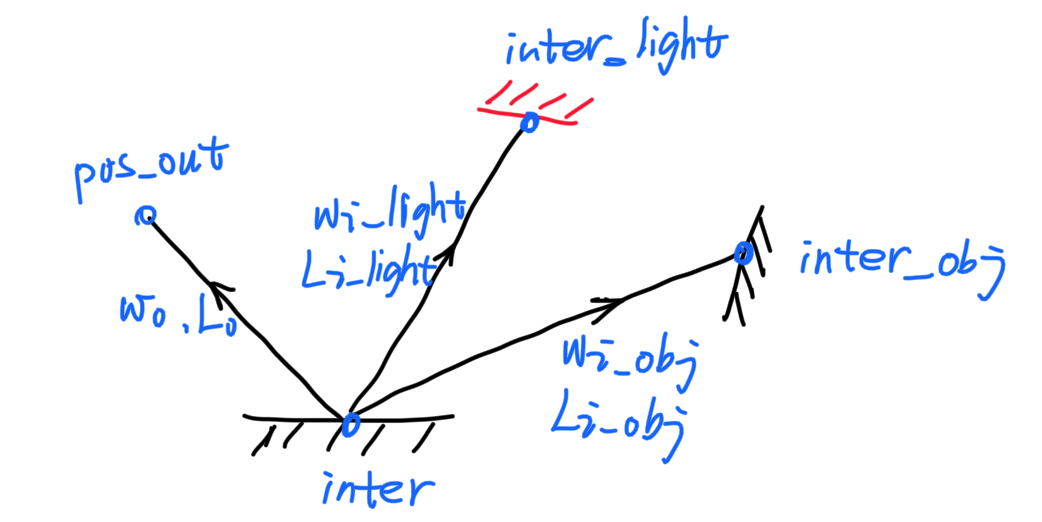
光路由许多的路径节点组成,路径节点主要包含一下信息:
- 交点信息:交点的位置,材质,法线等
- 入射,出射光线的 Radiance 和方向
- 使用了对光源采样,所以光路节点中会区分来自光源的入射光线和来自物体的入射光线
以下是一个路径节点的示意图:
在内存中的数据结构为:
struct PathNode {
/* 出射光线的信息 */
Eigen::Vector3f Lo{0.f, 0.f, 0.f}; /* 出射光线的 Radiance */
Direction wo = Direction::zero(); /* 出射光线的方向 */
Eigen::Vector3f pos_out{0.f, 0.f, 0.f}; /* 出射光线的端点 */
Intersection inter = Intersection::no_intersect(); /* 是否和物体有交点 */
/* 来自光源的入射光线 */
struct {
Eigen::Vector3f Li_light{0.f, 0.f, 0.f};
Direction wi_light = Direction::zero();
Intersection inter_light = Intersection::no_intersect(); /* 交点信息:材质,法线,位置等 */
} from_light;
/* 来自物体的入射光线 */
struct {
float RR{-1.f}; /* 记录俄罗斯轮盘赌的概率,方便 debug */
Eigen::Vector3f Li_obj{0.f, 0.f, 0.f};
Direction wi_obj = Direction::zero();
Intersection inter_obj = Intersection::no_intersect();
} from_obj;
};path tracing 的算法思路是:从摄像机向场景内投射光线,光线在物体之间弹射,递归地计算 Radiance
这个项目使用了对光源采样,所以需要区别对待发光体和普通物体
从摄像机投射光线,有以下几种情况:
情况1:没有与任何物体相交
最终的 Lo = 0
情况2:与光源相交
最终的 Lo = Light.Lo
情况3:与物体相交
这种情况,需要递归地计算,以俄罗斯轮盘赌来判断光线弹射是否终结
使用俄罗斯轮盘赌来控制弹射是否终结时,弹射次数期望的计算公式为:RR / (1 - RR) ^2
- 当 RR = 0.8 时,期望弹射 20 次
为什么要对光源进行采样:如果采用随机采样,则光线很难和光源相交——很多采样光线是无效的
如何基于光源采样:
- 在所有光源中随机选择一点作为光源的采样点
- 判断物体的采样点和光源的采样点之间是否有阻挡
- 将反射方程通过变换积分变量的方式,变成对光源面积做积分,计算出入射的 Radiance
光线和物体相交之后会发生弹射,由于误差的存在,计算出后下一步的交点可能仍然在当前交点附近,也就是光线在原地弹射。
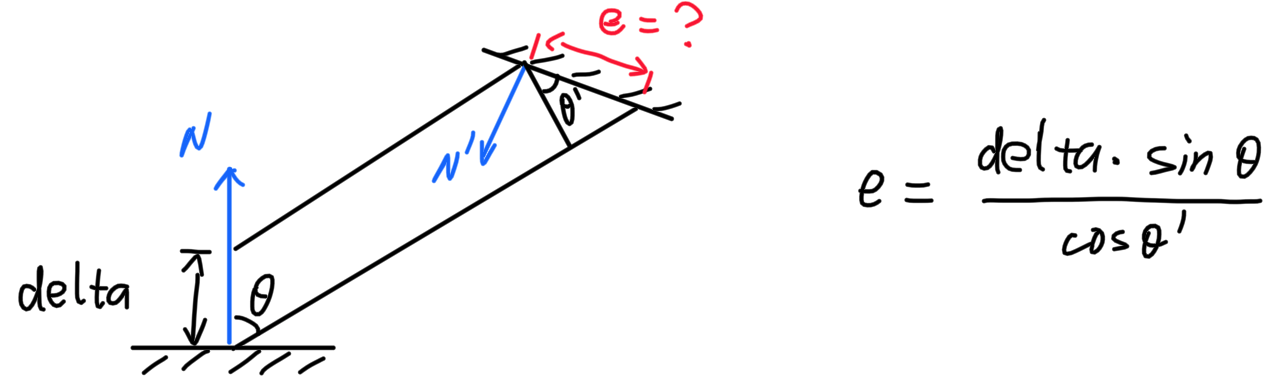
目前想到的解决办法是:让反射光线的原点关于物体法线做一个小的偏移:
这样做会有一个问题:弹射光线的交点也和原本的交点有了一个偏移,这个偏移如何计算:
使用蒙特卡洛积分来进行数值计算,n=1,反射方程变成:
$$
L_o = f_r L_i \cos\theta / pdf
$$
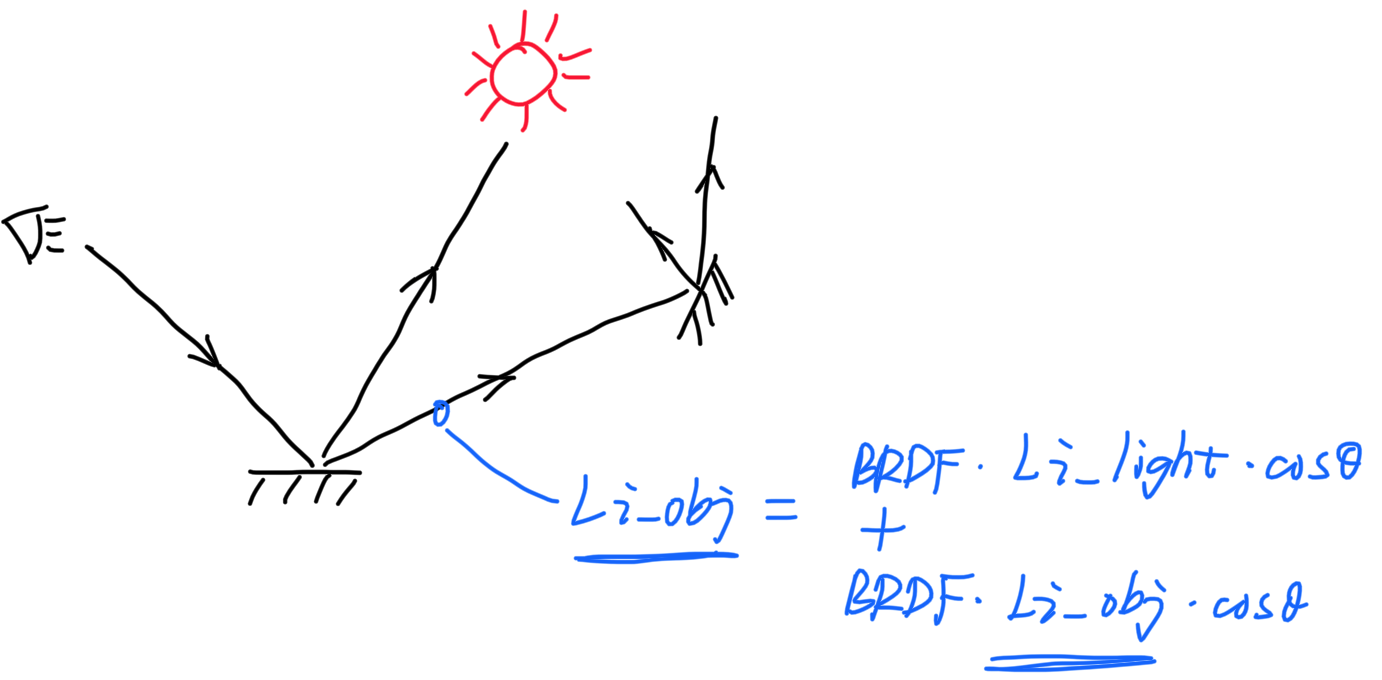
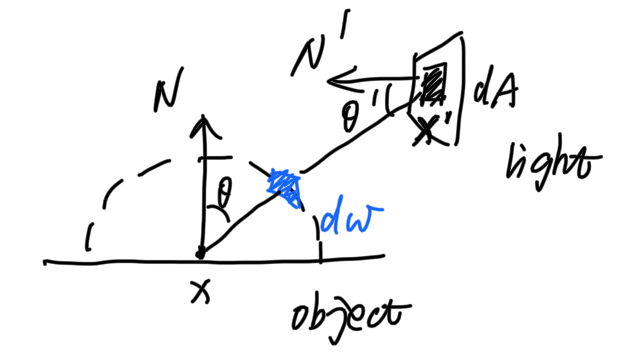
对于光源,使用了基于光源面积的采样,应该改变积分域:
积分变量之间存在着这样的关系: $$ dA \cos\theta' = d\omega (dis)^2 $$
对于来自光源的入射光线,反射方程为: $$ L_o = f_r L_i \cos\theta \frac{\cos\theta'}{||x' - x||^2} / pdf $$
光线在普通物体上弹射时,需要通过俄罗斯轮盘赌来判断是否继续弹射,改造后的反射方程为: $$ L_o = \frac{f_r L_i \cos\theta}{pdf * RR} $$
考虑了自发光,直接光照,间接光照的反射方程为: $$ L_o = L_E + f_r L_i \cos\theta \frac{\cos\theta'}{||x' - x||^2} / pdf
- \frac{f_r L_i \cos\theta}{pdf * RR} $$
一些实现的细节,踩坑的地方。
- 射线可能与包围盒平行,需要单独考虑
- 包围盒可能退化为点/线/面,这些情况下能否计算出正确的交点
- 计算射线和 BVH 交点时,如果射线和左右子树都有交点,则取离射线原点更近的交点
- 计算射线和三角形模型交点的方法:
- 首先以一个三角形为最小单元,建立起 BVH
- 通过 BVH 来计算交点
一定要小心使用 Catch2 的 SECTION,有些代码可能会被重复执行多次
构造函数最好显式初始化所有成员变量,让函数行为可控
class A{
public:
A(): _val(0) {}
private:
int _val;
};类成员不要通过其默认构造函数初始化,应该手动设置初始值,行为可控
class A{
private:
Eigen::Vector3f _vec{ 0.f, 0.f, 0.f };
};多使用工厂函数来创建对象,构造函数的表达性不强
不要在使用 class 的静态变量,包括全局变量,类静态成员,以及函数静态变量。因为这可能会引入两个问题
- 可能会抛出异常
- 构造函数的调用时机不明确
运行的静态变量,必须是 POD (Plain Old Data)的
- 光线追踪渲染器中,可以通过减少内存的
copy来优化执行效率;还可以减少内存的分配次数,比如shared_ptr的申请次数,以及vector等容器的扩容次数 - 误差是如何产生的?那些判断过程需要使用 epsilon,epsilon 的值应该定多大?滥用 epsilon 是否会额外引入误差?