TANS 2019-2020 Final Project

Description

This program is a basic implementation of simulation and recontruction of particles colliding events (proton-proton collision).
The collisions are generated in a region called collision diamond centered in the origin of a cartesian plane, where z is the beampipe direction.
A vertex detector is designed to determine the coordinates of the collision (primary vertex).
In this project only the z coordinate is being reconstructed.

Experimental Setup

The vertex detector is built of two cylindrical silicon pixel detectors, coaxial with the beampipe.
While often the interaction region is in a magnetic field, it is supposed that the field intensity and the distance from vertex to detectors is small enough to assume that the trajectories of charged particles are rectilinear (locally and with high momentum).
The vertex specification are:

The standard deviation in z is .
The standard deviation in x and y is .

The beampipe is made of Berilium and has a radius of 30 mm and a thickness of 0.8 mm.
The first pixel detector has a radius of 40 mm and a thickness of 0.2 mm.
The second pixel detector has a radius of 70 mm and a thickness of 0.2 mm.
Each one of the detectors is 270 mm long.
Hit points' smearing is based on a gaussian distribution with in z and in .
Multiple scattering can be simulated in the beampipe and silicon layers.

Simulation

Collision vertexes are generated with a normal distribution and particles follow the pseudorapidity and angle distribution from a given kinematic file. Multiplicity can be generated from different distributions (default: gaussian).
The vertex coordinates and multiplicity generated by generateVertex(double * ptc) are saved in an array double ptc[4].
The coordinates are then passed to the generateParticles(double *ptc, TClonesArray *particles, const uint8_t distType) where particles are generated by the defined distributions, then their coordinates are saved in a TClonesArray.
Particles' array is passed to intersect(double *ptc, TClonesArray *particles, TClonesArray *Hits, double width, double radius, double z_sm, double rho_sm, int randomNoise) where the intersection with the detector layer is calculated; the method accepts as inputs width, radius, z smearing, rho smearing and can also generate a number of random coordinates simulating noise and low energy particles.
Paricles which don't intersect are dropped to speed up computation. The result is a TClonesArray containing hits' coordinates expressed in cylindrical coordinates. The same is repeated for the second detector layer.
If multiple scattering is enabled, before any intersect, the method multipleScattering(TClonesArray *particles, double rmsTh) is called. This method modifies the particles' array by applying the rotation matrix to the scattering vector.
The simulation then fills a file called simulation.root with vertexes and hits arrays.

Interaction with detector layers

intersect(double *ptc, TClonesArray *particles, TClonesArray *Hits, double width, double radius, double z_sm, double rho_sm, int randomNoise) is the intersection method.
Given a primary vertex and a particles' array, a basic linear interpolation is computed to find the interaction point on the detector. The interaction point is then smeared by generating random values with a given mean and rms value. Detector noise can be generated specifying the number of random points, then the coordinates are generated following a normal distribution for z and .

multipleScattering(TClonesArray *particles, double rmsTh) is the multiple scattering method.
Given a particles' array and a rms angle value, a rotation matrix is built with the particle coordinates and then a scattering vector is computed via random generation of and values. The two are multiplied and the result are the new particle coordinates, which replace the originals in the array.

Reconstruction

The recontruction script reads the events from the previous simulation file to reconstruct the vertexes. The reconstruction is taking care of z coordinate only, since 3D recontruction with this setup is not as precise and the standard deviation on x and y is small enough.

Reconstruction procedure

Hits and vertexes are read from the simulation file in a for loop to process every event. The size of the reconstruction can be selected when calling the method.
Histograms relating hits and multiplicity, hits and Z are filled. Those will be used to compute efficiency.
The method to reconstruct z is then called.

Tracklet Algorithm

By reading hits from the arrays, filtering by angle is applied to reduce the following computation. The remaining hits are then passed to the tracklet class and correlated by findZVertex() which uses a simple linear interpolation to return the z.
Reconstructed z coordinates are added to a vector and filled in an histogram; from the histogram is extracted the mode value by getting the most frequent value via findMax(TH1I &data, const double &tol); a multiple maximum rejection and average is also implemented.
The mode value extracted is then averaged with the nearest values by the nearAvg() method, which selects the values in a neighborhood of a specified width. The value returned by this method is the definitive reconstructed z.

Statistics generation

The reconstruction process will print the resulting statistics, giving the user histograms on:

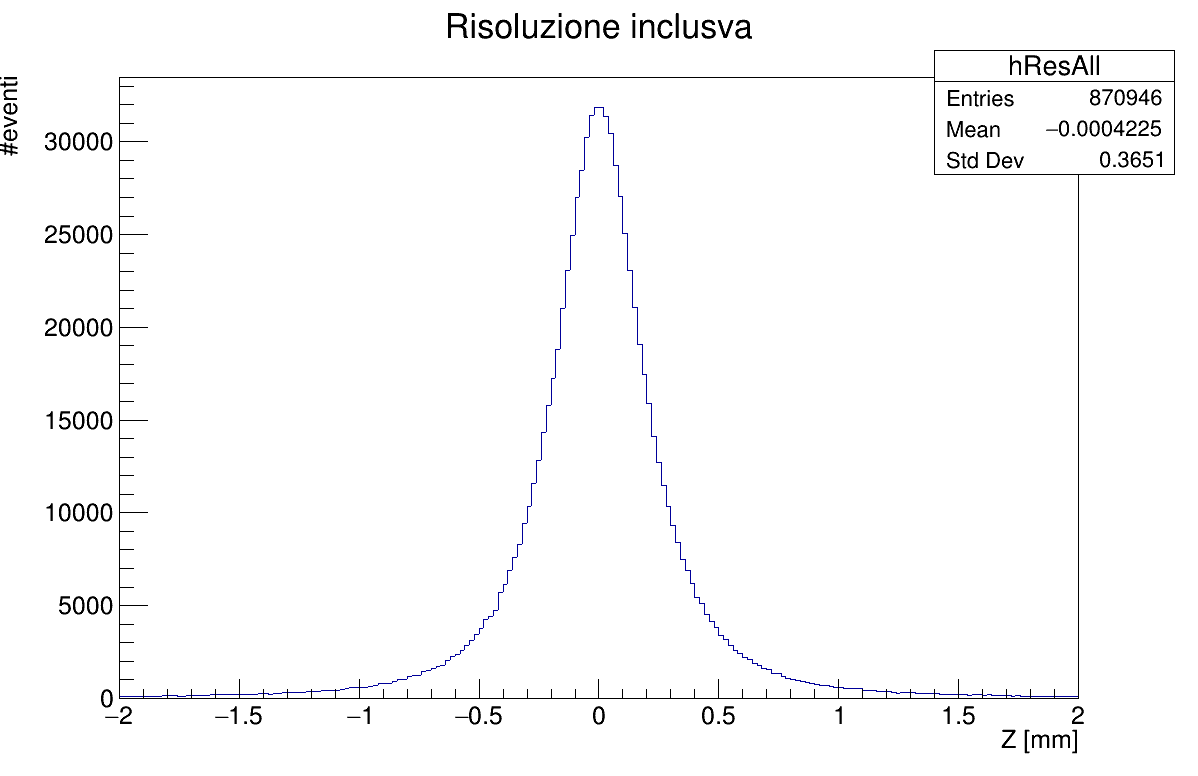
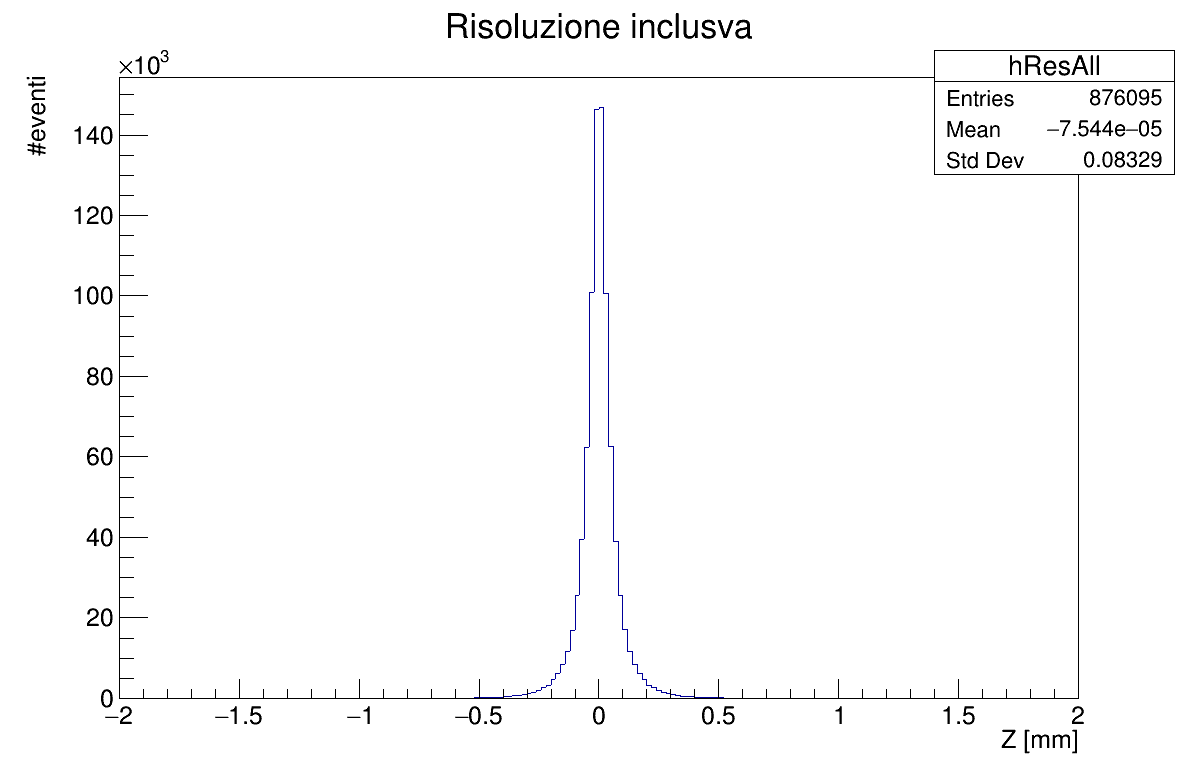
Vertex resolution distribution
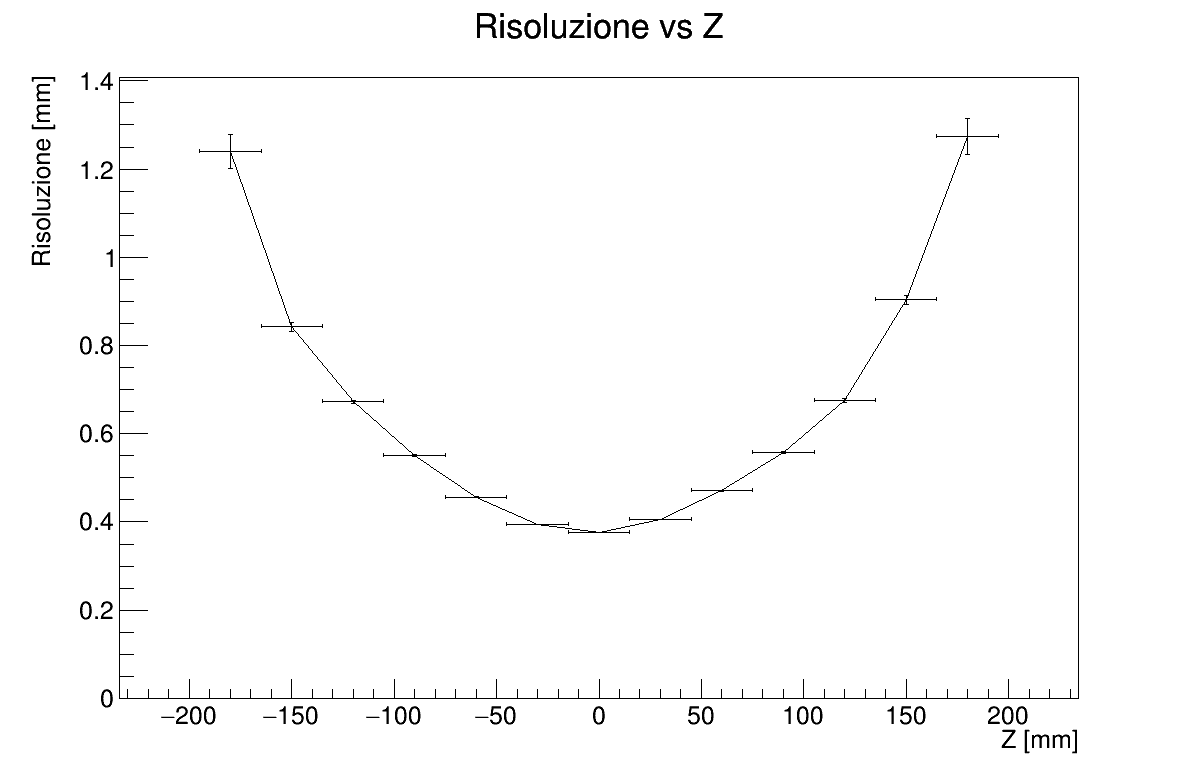
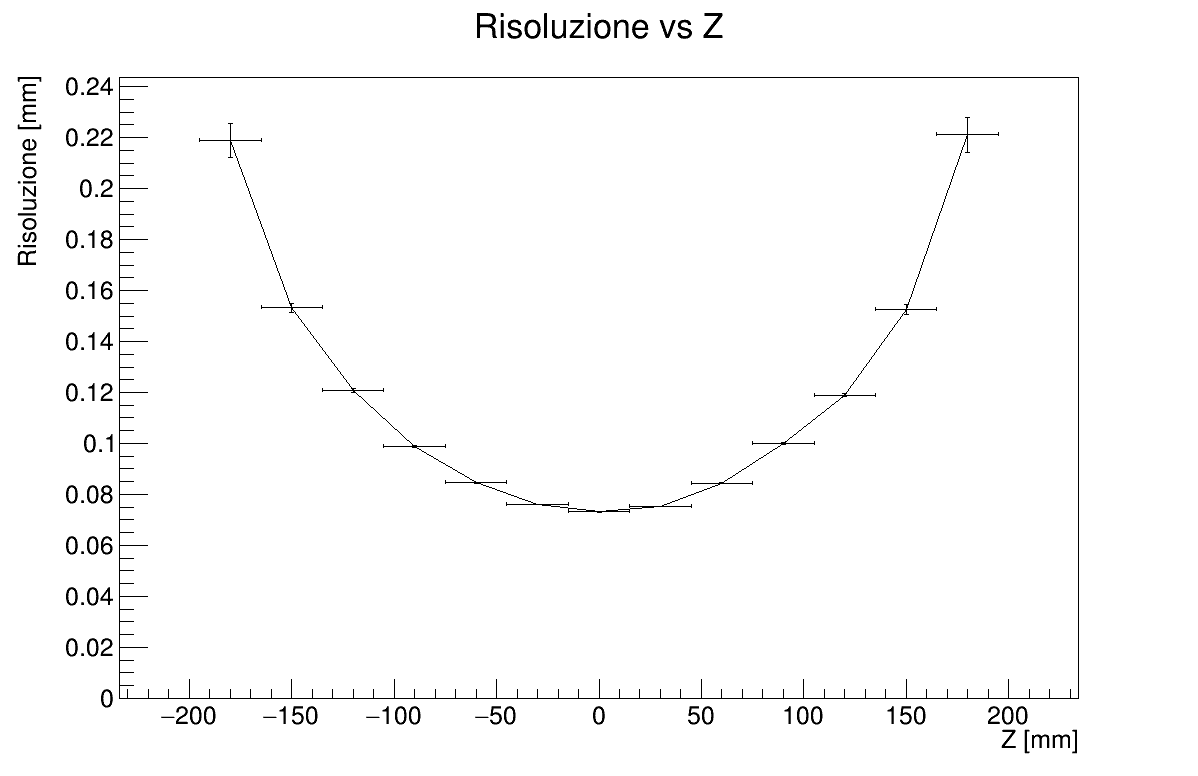
Resolution vs Z-axis
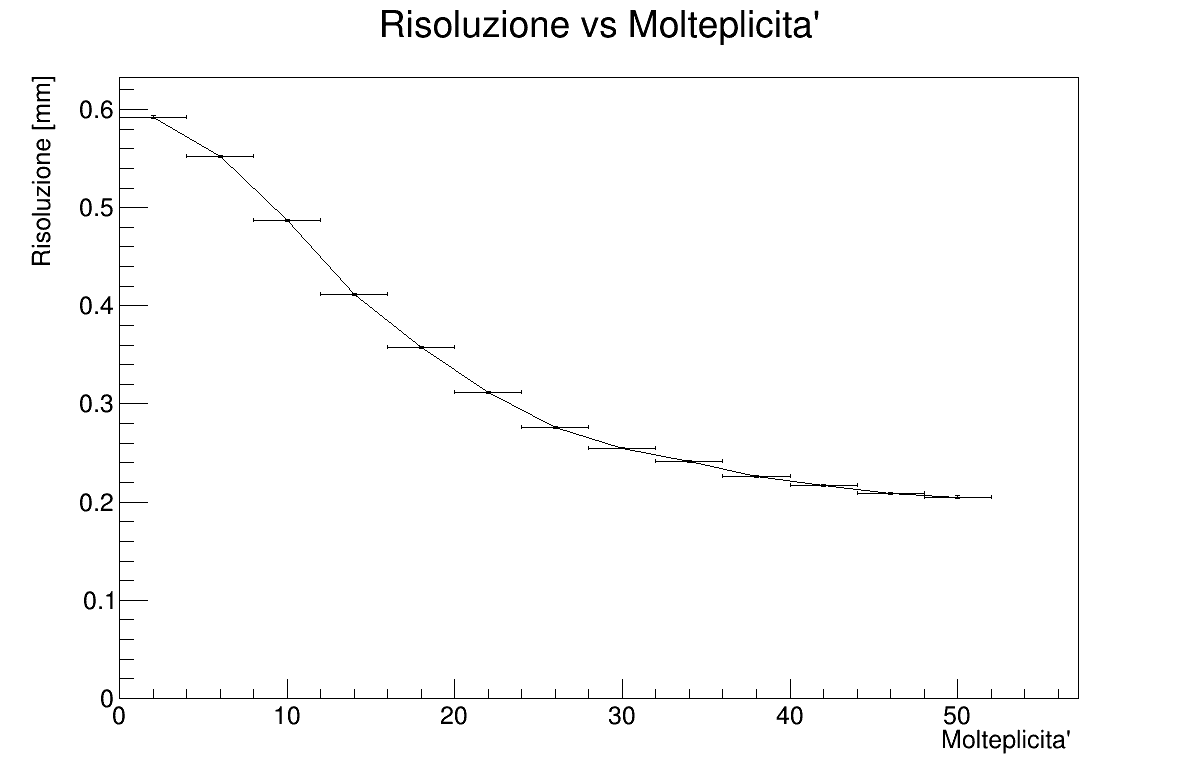
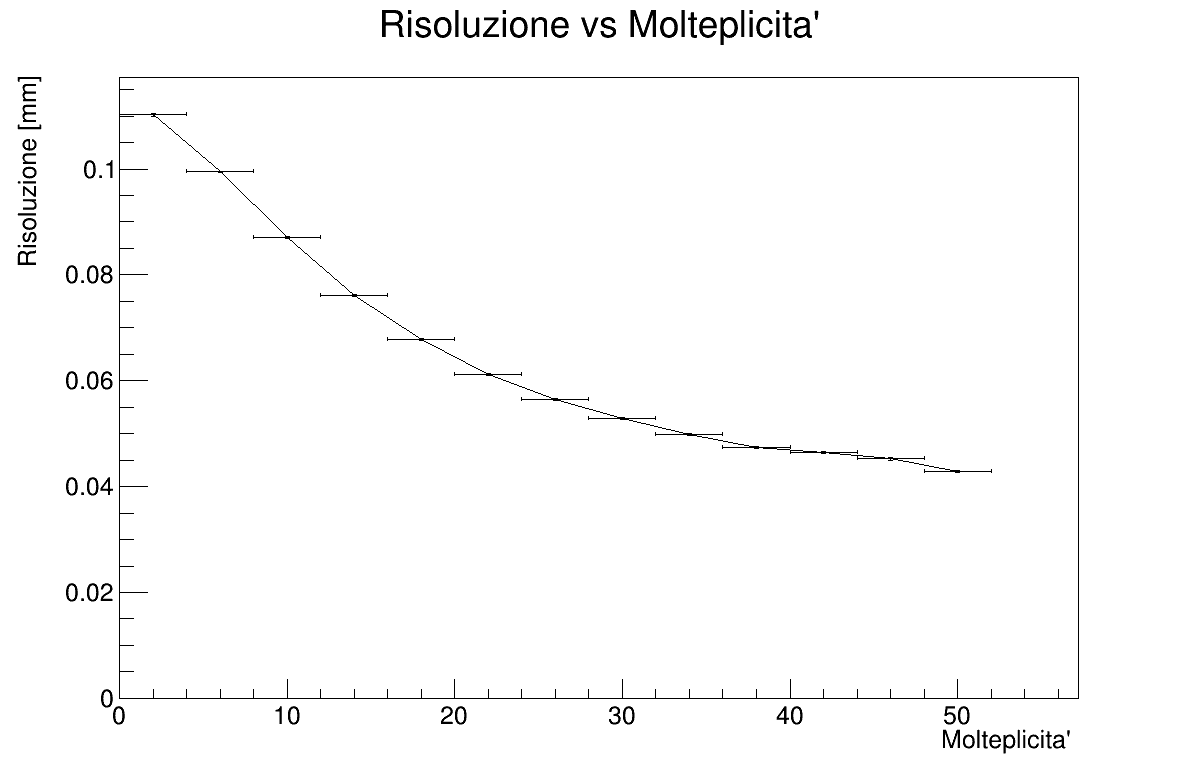
Resolution vs Multiplicity
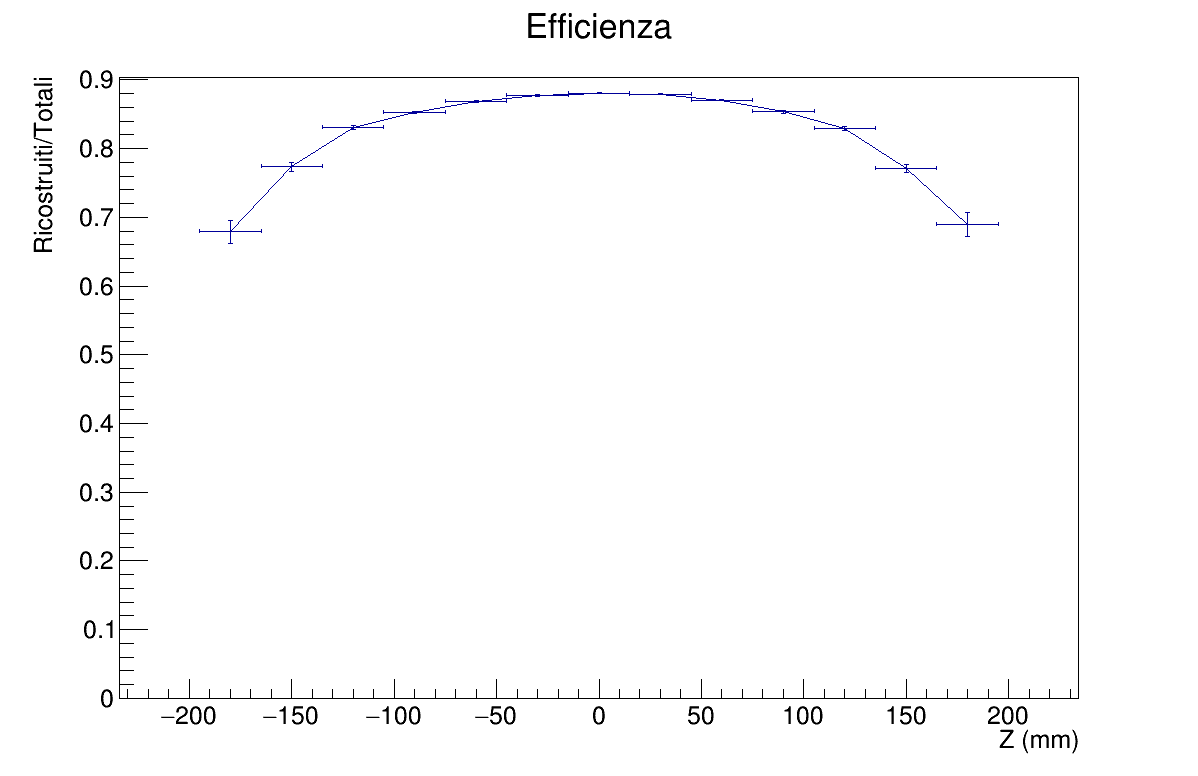
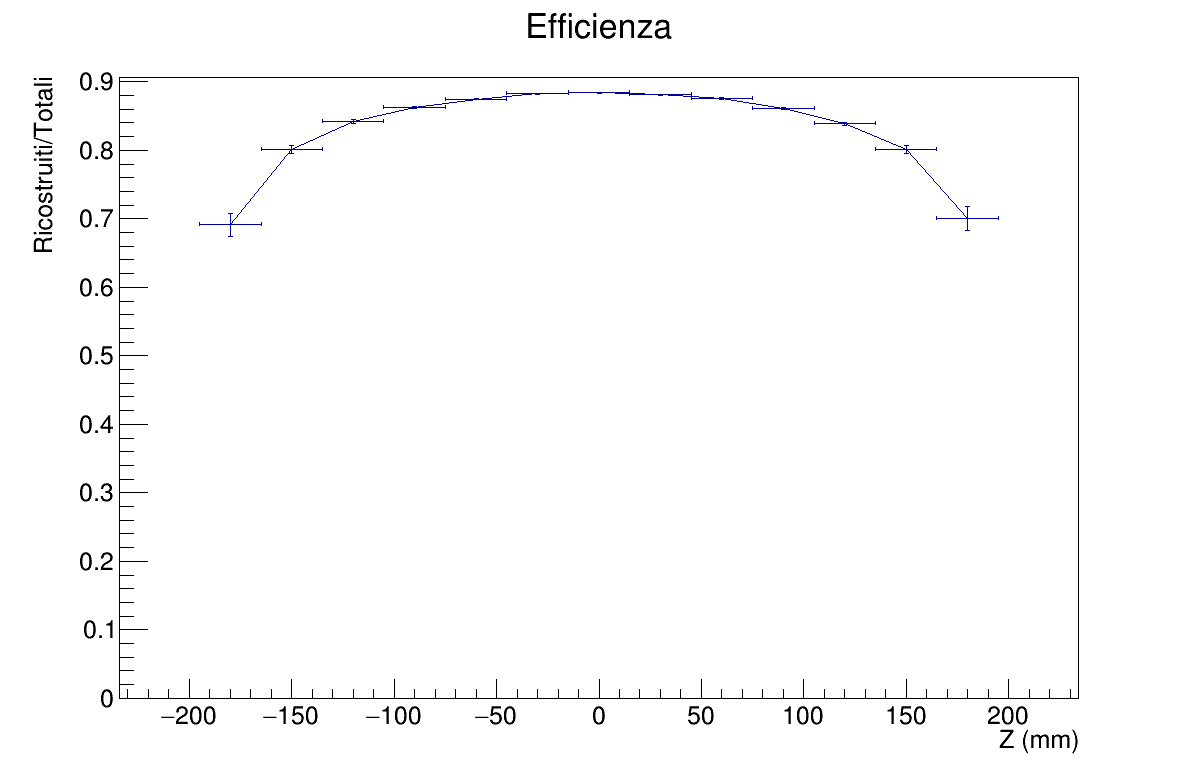
Efficiency vs Z-axis
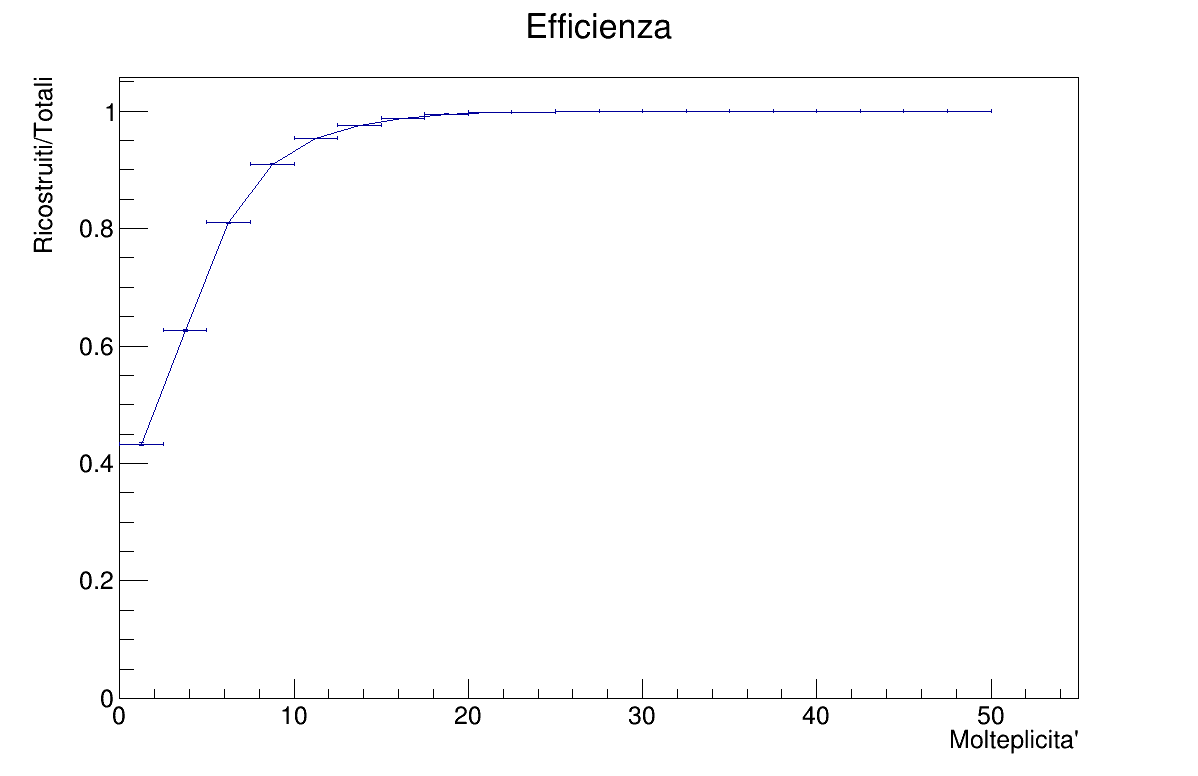
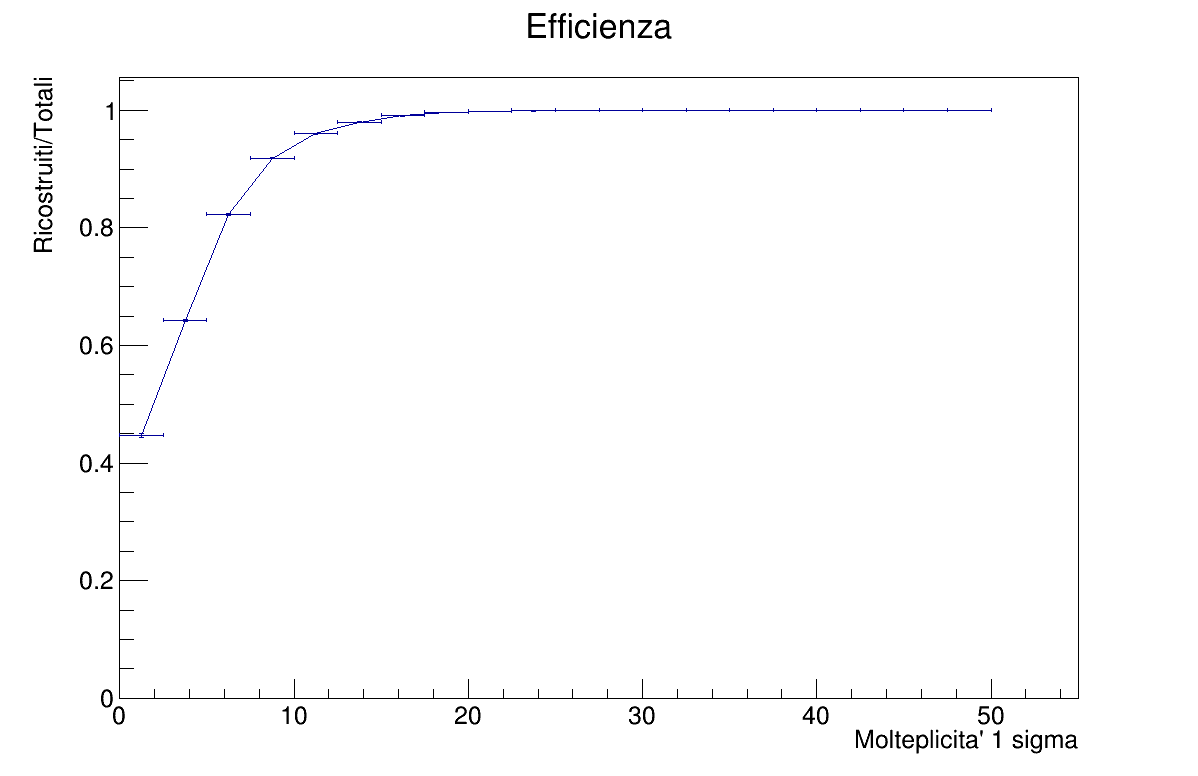
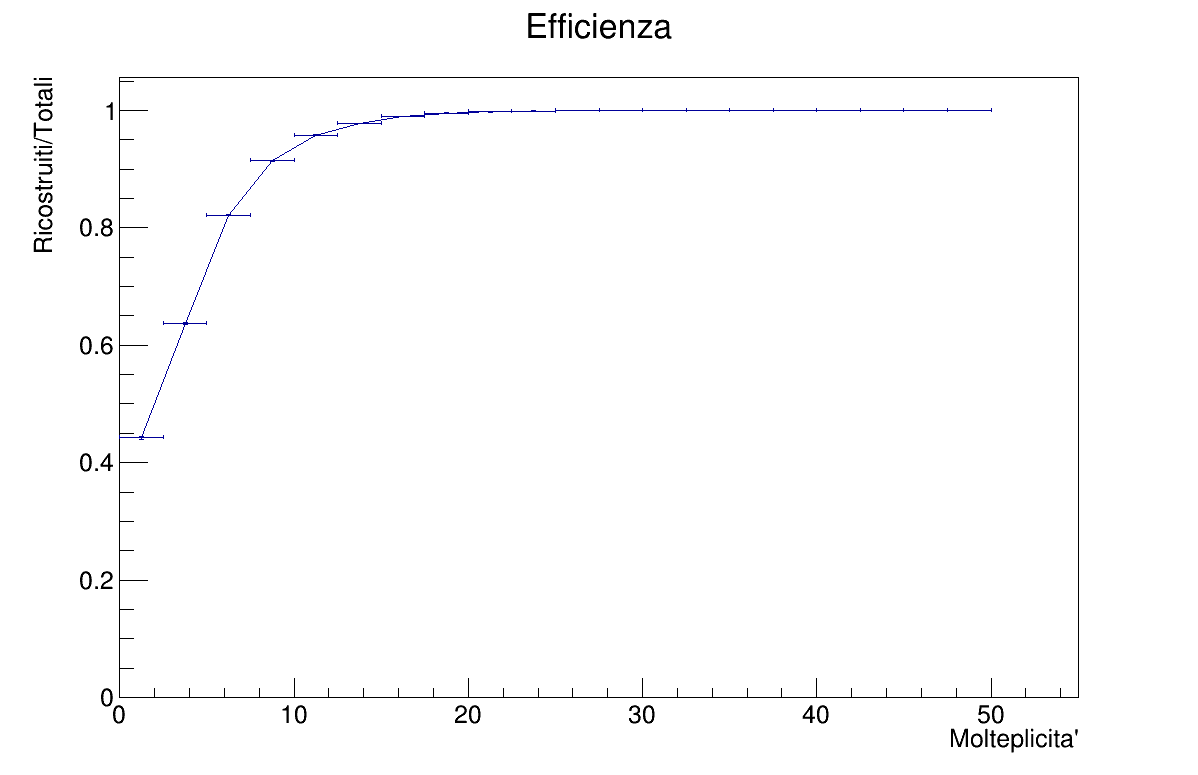
Efficiency vs Multiplicity

To get vertex distribution, the deviation between the generated and the reconstructed coordinate is calculated.
To get resolution vs Z-axis, a TGraphErrors is built by extracting rms and rms error from the deviation histograms, which have been filled during the reconstruction. The same procedure is applied to the resolution vs multiplicity chart.
Efficiency charts are instead built by evaluating reconstructed vs generated vertexes, then a TGraphAsymmErrors is drawn.

Results

Simulation and reconstruction parameters:

Multiple scattering enabled with
0 random noise hits
1'000'000 of events generated and reconstructed
Z tolerance of 1 mm
tolerance of 0.01 rad

The overall efficiency is 86.7%. The resolution is influenced by the multiplicity following an exponential function. In the Resolution vs Z graph is possible to see how the resolution is greatly increased near z=0, while diverging at the ends.
Regarding the efficiency, with higher multiplicity the algorithm is more efficient as expected. In terms of Z, efficiency is best when near the center with a plateau of 0.9, while degrading at the ends.

Histograms:

Total Resolution (distribution of deviation)
Resolution vs Multiplicity
Resolution vs Z
Efficiency (Reconstructed/Total) vs Multiplicity
Efficiency (Reconstructed/Total in ) vs Multiplicity
Efficiency (Reconstructed/Total) vs Z

With multiple scattering disabled:

Histograms:

Total Resolution (distribution of deviation)
Resolution vs Multiplicity
Resolution vs Z
Efficiency (Reconstructed/Total) vs Multiplicity
Efficiency (Reconstructed/Total in ) vs Multiplicity
Efficiency (Reconstructed/Total) vs Z

How to run

open a terminal
run git clone https://www.github.com/albydnc/tansSim to clone the project
change directory by typing cd ./tansSim
open root in terminal
run .L compile.cxx
run compile_simulation(), it takes a while
to run the simulation, simulation(true, 10) where true is enabling multiple scattering and 10 is the number of random noise points per layer
when it is complete, to reconstruct run recontruction("simulation.root",0,1,0.001), where arguments are filename, number of events to be processed, tolerance and minimum theta filter

Simulation and Reconstruction Performance

Testbench:

Ubuntu 20.04.1 LTS with 5.7.1 generic kernel
ROOT v6.23/01
Intel i7-8750H Laptop CPU
16GB DDR4 RAM
512GB NVMe SSD

With default settings, simulation of 1M events takes 30 seconds on average.
Reconstruction of 1M events takes 10 seconds on average.

Performance is greatly improved by using the C++11 STL data classes over TClonesArray. Simulation of 1M events is around 10 seconds average. 8x faster.
As for now (ROOT v6.23/01), TTree does not support std::vector<std::array<double,2>> so the development is not further going on. I will keep track of ROOT new releases to see if it will be supported.
Post opened on the ROOT forum regarding this issue.

Project Files Tree

project
+--- src
     +--- simulation.C
     +--- reconstruction.C
     +--- simulation_std.C
+--- lib
     +--- collision.h
     +--- collision.cxx
     +--- detector.h
     +--- detector.cxx
     +--- hit.h
     +--- hit.cxx
     +--- particle.h
     +--- particle.cxx
     +--- tracklet.h
     +--- tracklet.cxx
+--- data
     +--- kinem.root
+--- img
+--- tex
+- compile.cxx
+- compile_std.cxx

Libraries Description:

collision: generate vertex, multiplicity and direction

ImportKinem(): import kinematic file
getDir(): generate particle direction
getCoordinates() get vertex coordinates and multiplicity
generateCollision() generate vertex and multiplicity

detector: intersect with detector layers, random noise and multiple scattering

intersect() intersect with detector layer
randomHits() generate random hits
multipleScattering() multiple scattering generator

hit: hit coordinates, angle difference method

getTheta() get theta coordinate
getZ() get z coordinate
deltaTheta() difference between theta angles

particle: particle direction, transport layer

getTheta()
getPhi()
setTheta()
setPhi()

tracklet: z-vertex finder

findZVertex() find z vertex by generating tracklets

Written by Alberto Perro - 2020

albydnc/tansSim