This project implements a solver for the 8-Puzzle Problem using the A* search algorithm, enabling use of two different heuristics.
The heuristic #2 implementation is able to find solutions of great depth (number of steps) -- e.g. 23 steps -- very quickly.
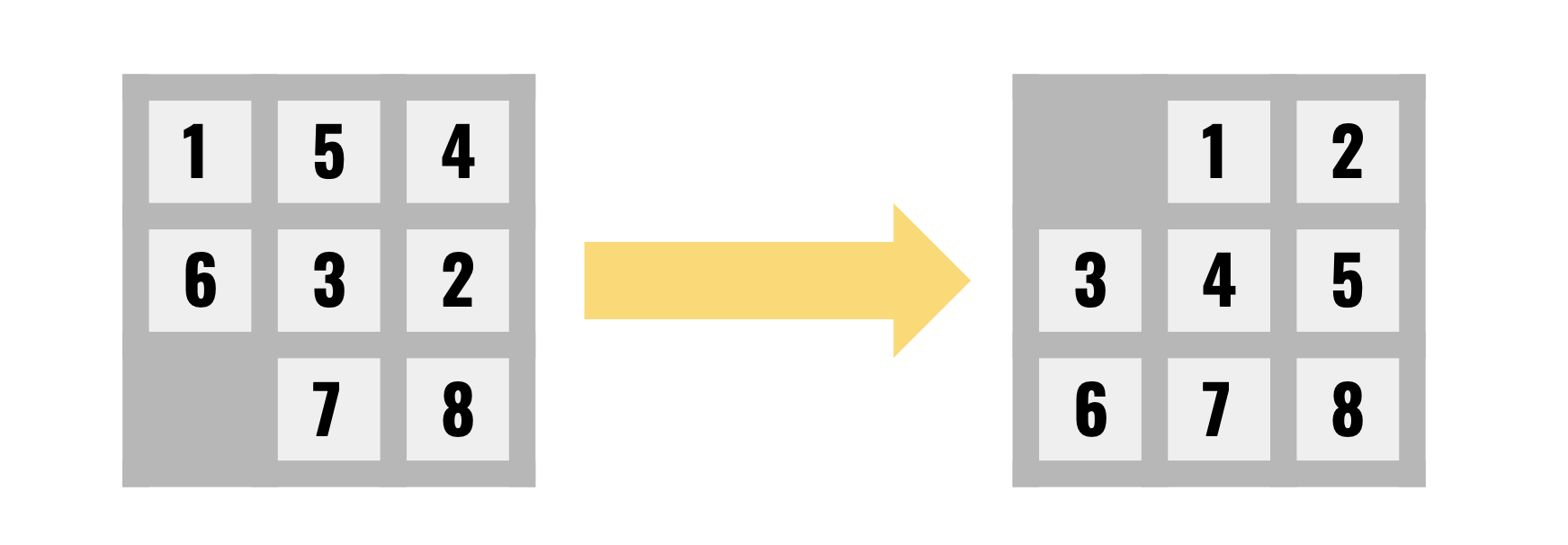
The objective of the 8-Puzzle Problem is to find a step-by-step solution to a puzzle with 8 numbers, where the only movements allowed are single permutations between neighboring elements to the empty space (represented as 0). For example,
A solution to the 8-Puzzle Problem is of the form
0 1 2
3 4 5
6 7 8
where 0 represents the empty tile.
This project was tested on a Python 3.8 environment. In order to run the solver, type in the command
python solve_puzzle.py
Upon entry in the command line interface, you may choose between two modes of operation: solving a puzzle drawn at random or a puzzle input from the command line of the format (for instance):
5 4 1
7 6 3
8 2 0
After the puzzle is displayed, it is possible to choose between two search heuristics to implement in the A* search:
h1 = Number of Misplaced Tiles
h2 = Manhattan Distance
The program then outputs (if the puzzle is a solvable puzzle) each step to solve the puzzle.
The program also displays the final search cost (number of nodes needed) to solve the puzzle and the time in seconds it took to solve it.
Sample program outputs are available in the /output folder.
This heuristic counts the number of tiles that are not in the original place that they should be.
This heuristic sums the taxicab distances of the tiles from their location to the original place they should be.
More outputs (of greater depth) are found in /output.
CS 4200 Project 1
8-Puzzle Solver
--------------------------
Select option:
[1] Solve random puzzle
[2] Solve puzzle from input
[3] Exit
2
Type in your puzzle in 3 lines:
1 4 2
3 7 5
0 6 8
Puzzle:
1 4 2
3 7 5
0 6 8
Select heuristic to solve:
[1] h1 = Number of Misplaced Tiles
[2] h2 = Manhattan Distance
2
Solution Found
Initial state:
1 4 2
3 7 5
0 6 8
Step #1: move left
1 4 2
3 7 5
6 0 8
Step #2: move down
1 4 2
3 0 5
6 7 8
Step #3: move down
1 0 2
3 4 5
6 7 8
Step #4: move right
0 1 2
3 4 5
6 7 8
Solution Depth: 4
Search Cost for heuristic h2: 10 nodes
Search Time: 0.0017 seconds
--------------------------