hasklog: A Haskell repository from cimbul

Hasklog

Hasklog is a interpreter and compiler for a subset of Prolog. Hasklog is written in Haskell. Its features include:

Full and correct support for resolution of logical goals, including recursive rules and nested structures
Negation as a failure
A compiler targeting a simplified version of the Warren Abstract Machine (WAM), as defined in Hasan Ait-Kaci’s reconstruction
Lists and numbers (but unfortunately no math at this point)
User-defined operators

Contents

Hasklog ci-badge ghc-badge stack-badge license-badge
Using Hasklog
- Setup
- Tests
- Usage
- Examples
Technical Description
Reference

Using Hasklog

Setup

Hasklog can be built with Cabal or Stack. The instructions below assume you are using Stack.

Run the following commands inside the directory where you unpacked Hasklog:

$ stack build

Now you can run Hasklog from the Stack build directory:

$ stack run

Or install the hasklog executable on your system:

$ stack install
$ hasklog  # Assuming you have ~/.local/bin in your PATH

Tests

To run the Hasklog unit tests:

$ stack test

Usage

When you first start Hasklog, the program presents an interactive prompt where you can run queries and built-in commands:

$ hasklog
?-

You can read in files using the consult/1 command. Alternatively, you can specify files to consult through the command line:

$ hasklog file1 file2
?-

When you are finished with your session, press Control+D to quit.

Examples

The following sections contain example sessions using the files provided in the examples/ directory.

Family Tree Database

?- consult('examples/family_trees').
true.
?- parent_child(bill, ted).
true.
?- parent_child(ted, bill).
false.
?- parent_child(Who, bob).
Who = bill ? ;

Who = mary ? ;

false.
?- ancestor_descendent(kim, Whom).
Whom = george ? ;

Whom = mary ? ;

Whom = ted ? ;

Whom = bob ? ;

false.
?- ancestor_descendent(Who, ted).
Who = bill ? ;

Who = mary ? ;

Who = george ? ;

Who = susan ? ;

Who = dave ? ;

Who = kim ? ;

false.
?- ^D

List Processing

?- consult('examples/lists').
true.
?- member(What, [a,b,c]).
What = a ? ;

What = b ? ;

What = c ? ;

false.
?- append([a,b,c], [d,e,f], What).
What = [a,b,c,d,e,f] ? ;

false.
?- append(What, [d,e,f], [a,b,c,d,e,f]).
What = [a,b,c] ? ;

false.
?- reverse([a,b,c,d]).
What = [d,c,b,a] ? ;

false.
?- ^D

Compiling

?- consult('examples/lists').
true.
?- consult('examples/family_trees').
true.
?- consult('examples/crazy_structures').
true.
?- compile('examples/everything').
true.
?- ^D

At the end of this session, there should be a file named everything.wam in the examples/ directory. It will contain WAM instructions in text format for all the predicates defined in all three examples files.

Technical Description

Architecture

Hasklog is roughly divided into a parser, interpreter, and compiler units as shown in the figure below. The job of each of these units is described in the following sections.

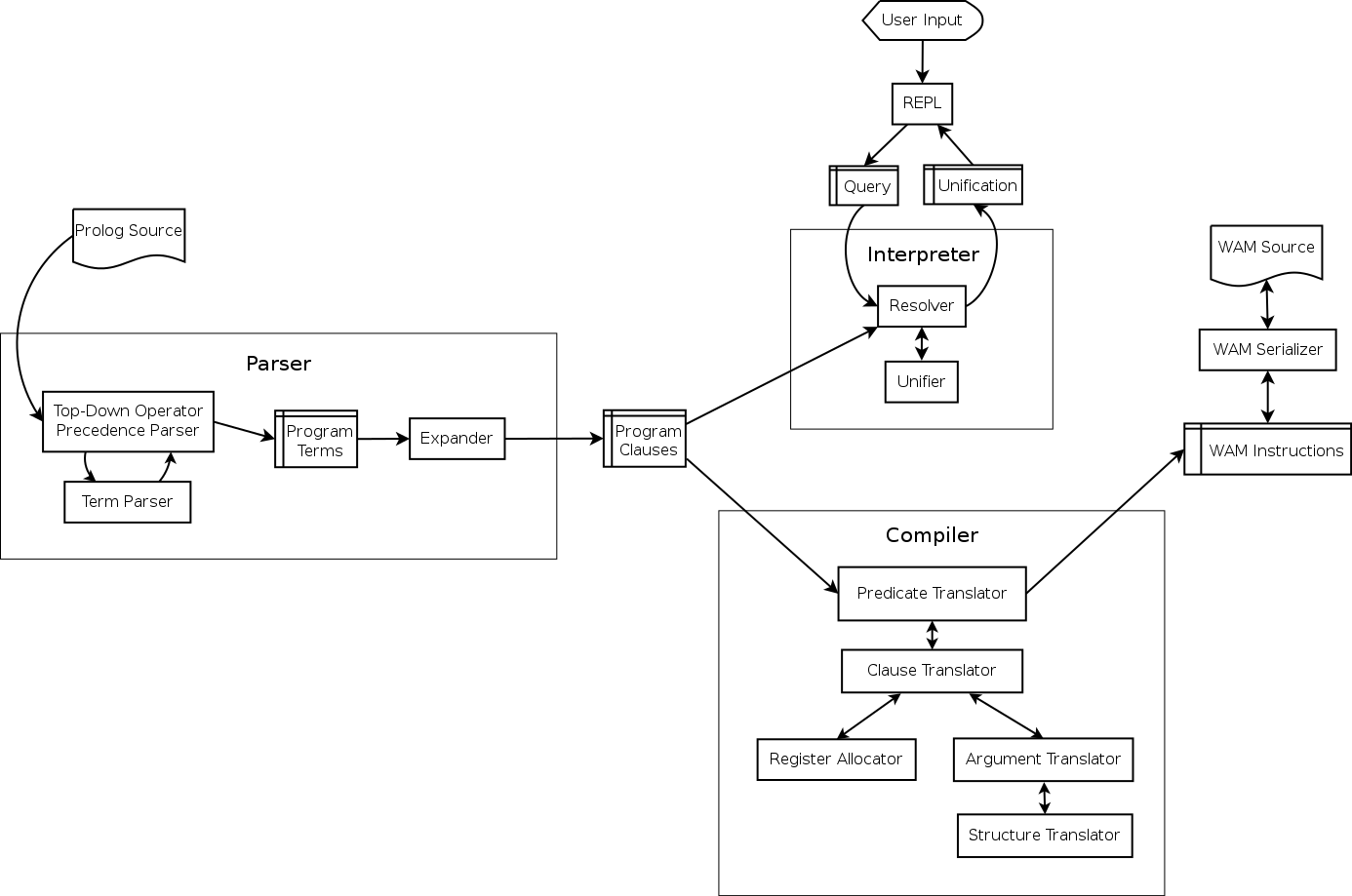
Architecture diagram. This version is slightly simplified. The interpreter is actually involved in parsing program clauses, so that directives in the source file (such as op/3 definitions and consult/1 directives) can be executed as they are read. Also, the compiler is run by the interpreter as a built-in predicate. The internal architectures are still accurate.

Parser

The parser is defined in src/Hasklog/Parser.hs. Its job is to transform the concrete representation of Prolog rules into a list of rule data structures. We can divide this task into two levels: parsing rules, and parsing terms.

Rules

Consider the following input:

foo(X) :- bar(X, Y).
foo(a).
bar(Z, Z).

This will be transformed into a list of data structures of the form:

\mathbf{DefiniteClause} \; h \; [g_1, g_2, \ldots, g_n],

where h is the representation of the head of the clause, and g_n is the representation of goal n in the body. Facts (heads with no body) are represented in the same form, but the list of goals is empty.

Queries and directives (rules with no heads) are represented in the form:

\mathbf{GoalClause} \; [g_1, g_2, \ldots, g_n].

Terms

The next problem is how to represent the terms in the head and body of rules themselves. A term is one of:

An atom: a, foo, 'with Quotes!', –>
A variable: X, SomeVar
A number: 123
A compound term: f(a,b), p(X, h(f(a), b))

These are represented in the following forms:

\mathbf{Atom}\; a
\mathbf{Variable}\; v
\mathbf{Number}\; n
\mathbf{CompoundTerm}\; f \; [t_1, t_2, \ldots, t_n]

where:

a, v, and f are the string representations of the atom, variable, and functor, respectively,
n is the integer represented by the number token, and
t_n is the nth subterm of the compound term.

Because compound terms contain other terms, the overall structure of parsed terms is a tree.

A final issue is how to deal with operators. Hasklog supports user-defined operators, which are simply functors of arity 1 or 2 that are written in prefix, postfix, or infix notation. For example, the expression a :- b is really a compound term with functor :-/2, and can also be written as :-(a, b). Hasklog uses a top-down operator precedence parser to parse operations, which are then transformed into their term representation.

Interpreter

The interpreter is defined in src/Hasklog/Interpreter.hs. Its job is to find logical solutions to queries using rules defined in a program. For example, consider the program:

parent_child(bill, ted).
parent_child(bill, bob).
parent_child(mary, ted).
parent_child(mary, bob).
parent_child(george, mary).
parent_child(susan, mary).

female(mary).
female(susan).
male(bill).
male(ted).
male(bob).
male(george).

mother_child(Mother, Child) :- female(Mother), parent_child(Mother, Child).
father_child(Father, Child) :- male(Father), parent_child(Father, Child).

Some queries that could be performed on this program include:

?- mother_child(susan, ted). – Is susan the mother of ted?
?- father_child(Who, mary). – Who is the father of mary?

To properly match these queries to rules in the program, we need two pieces: unification and resolution.

Unification

Unification is the process of substituting variables in two terms so that they match. For instance, f(X, b) can be unified with f(g(a), Y) by setting X = g(a) and Y = b, so that both terms are equal to f(g(a), b).

Unification is essentially the process of walking two term trees simultaneously and matching variables in one tree to the corresponding term in the other tree. We also have to obey a few rules:

A variable can only have one substitution. We cannot unify f(X, X) ~ f(a, b), because that would require setting X = a and X = b at the same time.
Only variables can be substituted. We cannot unify f(a) ~ f(b) by substituting a = b.
A variable cannot unify with a compound term that it occurs in (occurs check). We cannot unify X ~ f(a, X), because that would produce a cyclic term.

In many cases, unification is impossible, so we have to handle failure appropriately.

Resolution

The heart of Prolog is resolution. Resolution is an logical inference rule that can be used to solve the satisfiability problem for Horn formulas.

Consider a query:

?- g1, g2, ..., gn.

where g_n are independent goals in the query. We can determine whether all the goals are true by trying to prove any of them wrong. If none of them can be proved wrong, then they are all true. Turning this into logical form:

\begin{aligned}
& \neg(g_1 \wedge g_2 \wedge \ldots \wedge g_n) \\
=\; &\neg g_1 \vee \neg g_2 \vee \ldots \vee \neg g_n\end{aligned}

Now assume we have a rule:

g1 :- h1, h2, ..., hn

We can represent this in logical form as:

\begin{aligned}
& g_1 \leftarrow h_1 \wedge h_2 \wedge \ldots \wedge h_m \\
=\; & g_1 \vee \neg (h_1 \wedge h_2 \wedge \ldots \wedge h_m) \\
=\; & g_1 \vee \neg h_1 \vee \neg h_2 \vee \ldots \vee \neg h_m\end{aligned}

If we assume that both our goal and this rule are true, then we have:

\begin{aligned}
& (g_1 \vee \neg h_1 \vee \neg h_2 \vee \ldots \vee \neg h_m) \wedge (\neg g_1 \vee \neg g_2 \vee \ldots \vee \neg g_n) \\
=\; & (g_1 \vee \neg (h_1 \wedge h_2 \wedge \ldots \wedge h_m)) \wedge (\neg g_1 \vee \neg (g_2 \wedge \ldots \wedge g_n))
\end{aligned}

Now notice that if g_1 is true, then \neg g_1 would be false and \neg (g_2 \wedge \ldots \wedge g_n) would have to be true. If g_1 were false, then \neg (h_1 \wedge \ldots \wedge h_n) would have to be true. In other words, one of the non-g_1 terms must be true no matter what g_1 is, so we can eliminate g_1 altogether and get:

\begin{aligned}
& \neg (h_1 \wedge h_2 \wedge \ldots \wedge h_m) \wedge \neg (g_2 \wedge \ldots \wedge g_n) \\
=\; & \neg h_1 \vee \neg h_2 \vee \ldots \vee \neg h_m \vee \neg g_2 \vee \ldots \vee \neg g_n
\end{aligned}

This last step is “resolution" proper. We now have a new set of goals, and we can repeat the procedure on this new set. We repeat until we either eliminate all the variables, proving our negation false and the original goals true, or until we have no rules left to resolve with, proving our negation true and the original goals false.

In summary, the steps of resolution are:

Negate the original goal clause.
Find a rule to unify with. If no rules unify, then fail.
Resolve against that rule to generate a new goal clause.
If nothing is left, succeed. Otherwise, repeat from step 2.

This is the basic algorithm used by Hasklog, except that it also has to deal with the question of which rule to unify with when there are several possible alternatives. It handles this by (lazily) taking all possible paths and concatenating all the results into a single list. The result takes the same space complexity as so-called “backtracking" algorithms, but in a much more straightforward manner.

Compiler

The compiler is defined in src/Hasklog/Compiler.hs. Its job is to take the rules in a program and translate them to a series of instructions for the Warren Abstract Machine (WAM). The details of the WAM are much too complicated to lay out here, but they can be found in Warren’s Abstract Machine: A Tutorial Reconstruction by Hasan Ait-Kaci (here). The version of the WAM targeted by Hasklog is the one laid out in chapters 1-3 of that book. It does not include the many optimizations in chapter 4.

A simplified view of the job of the compiler is to take the rules and define them as callable procedures. These procedures are passed arguments through predefined registers. A rule of the form:

p(a1, a2, ..., an) :- q1(b1, b2, ..., bm), q2(...), ..., qn(...).

does the following:

Allocate space on the stack to store variables
Extract the arguments a_1, \ldots, a_n of p/n and pull them onto the stack.
Pull the arguments b_1, \ldots, b_m of q_1/m from the stack and put them in registers, and call q_1/m
Do the same for the rest of the goals.

While arguments, which contain references to terms in memory, are being moved from the stack to registers, their values are being unified. If unification fails, the whole rule fails. If more rules are possible, then the machine will try the other alternatives.

The compiler has to determine the right instructions in the right order to make this happen. Some examples of instructions are:

allocate 5
get_variable Y4 A1
get_value Y4 A2
put_variable Y3 A2
put_structure f/2 A3
unify_value X4
unify_value Y2
deallocate

where terms like X1, A2, and Y4 denote temporary registers, argument registers, and stack locations, respectively.

Some of the complications the compiler has to deal with include:

Assigning variables (and partially constructed structures) to appropriate registers.
Deciding whether to keep variables in the stack or in temporary registers.
Ordering the construction of nested terms so that they are constructed before the terms that contain them.

Reference

The following built-in commands are available for you to use in Hasklog:

consult(+Filename)

Read the Prolog source file “<Filename>.pl" into the current session.

compile(+Filename)

Compile all the predicates defined in the current session into WAM code, and dump the compiled output to “<Filename>.wam".

not Goal

Negation as a failure: try to resolve Goal. Fail if a resolution is found, otherwise succeed.

true

Succeed without triggering any unification.

fail

Fail the current rule immediately.

op(+Precedence, +Type, +Symbol)

Define a new operator Symbol with precedence Precedence and fixity and associativity defined by Type. Valid values for Type are:

fx: A non-associative prefix operator.
fy: A right-associative prefix operator.
xf: A non-associative postfix operator.
yf: A left-associative prefix operator.
xfx: A non-associative infix operator.
xfy: A right-associative infix operator.
yfx: A left-associative infix operator.

cimbul/hasklog