duolu/pyrotation

A Python package to help teach and learn the math of 3D rotation.

pyrotation

This repository is a Python package to help teach and learn the math of 3D rotation. It has two modules:

• pyrotation_demo.py - contains GUI based interactive demo of 3D rotation of reference frame.
• pyrotation.py - contains the core class and routines for representation and operation of 3D rotation.

Both modules are tested on Python 3.6, NumPy 1.19, Matplotlib 3.1.2.

See the slides to learn the representations of 3D rotation.

pyrotation_demo.py

The pyrotation_demo module provides four interactive GUI visualizers based on the matplotlib, corresponding to the four representations of the 3D rotation implemented in the pyrotation module. Users can drag sliders to directly change parameters of the representation and the corresponding rotation of reference frame is shown in real-time. This demo is mainly made for learning how 3D rotation work.

This module requires numpy, matplotlib, and the pyrotation module.

pyrotation.py

The pyrotation module provides four different representations of a 3D rotation as well as corresponding operations on these representations:

• Angle-axis - represented as a numpy 3-dimensional vector u, where its direction is the axis and its length is the angle (the angle could be negative, which means the rotation uses the opposite direction of the vector). The rotation follows the right-hand rule.
• Euler angles (in z-y'-x" intrinsic convention) - represented as a tuple of three angles (z, y, x). These angles are also called Tait-Bryan angles, or (yaw, pitch, roll) angles. There are other conventions of Euler angles and only this specific notation is implemented and used in the demo.
• Rotation matrix - represented as a numpy 3-by-3 matrix R.
• Unit quaternion - represented as an object q of a custom quaternion class defined in the pyrotation module. The quaternion is in Hamiltonian convetion, i.e., (qw, qx, qy, qz).

This module requires numpy. In all cases, coordinate of a 3D point is represented as a numpy 3-dimensional vector. Array of 3D points is represented as numpy 3-by-n matrix, where n is the number of points. The coordinate reference frame is right-handed.

Getting Started

Installation

Just download pyrotation.py and pyrotation_demo.py, and run.

Usage of the pyrotation_demo module

Put both pyrotation.py and pyrotation_demo.py into the same folder, and launch the demo using the following command.

$ python3 ./pyrotation_demo.py [mode]

The "mode" can be one of the following:

• "u" or "angle_axis" - angle-axis (default if mode is not given)
• "e" or "euler" - Euler angles (in z-y'-x" intrinsic convention)
• "r" or "R" or "rotation_matrix" - rotation matrix
• "q" or "quaternion" - unit quaternion

For example, if the following command is used,

$ python3 ./pyrotation_demo.py q

Then the demo with quaternion is shown.

Common explanations:

1. In all demoes, the axes uses this color settings.

   • the x-axis is red.
   • the y-axis is green.
   • the z-axis is blue.

2. The three axes of the original reference frame are represented in dashed lines with black and color alternation, and the rotated reference frame are represented in solid lines with colors.

3. A solid disk on the XOY plane in the original reference frame is shown to represent the "ground"

Demo of the Angle-Axis Representation of a 3D Rotation

Explanations:

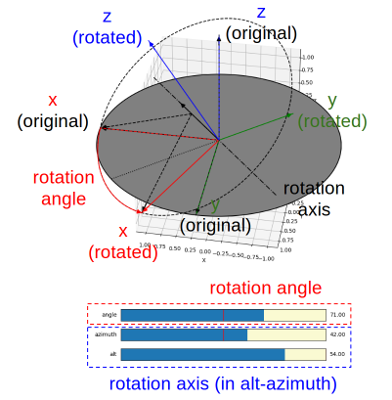
1. In the demo GUI, the rotation axis is represented in a dotted and dashed line through the origin. The rotation vector, i.e., the vector u, is shown as a solid black arrow on the axis. The projection of the axis on the ground is shown as a dotted line.

2. Besides, a dashed circle is shown, where the rotation axis is through the center of the circle and perpendicular to the plane of the circle. Two dashed arrows are on this plane pointing from the center of the circle to the original and rotated x-axis. On the circle, a red arc with arrow shows the rotation angle, pointing from the original x-axis to the rotated x-axis. Together they show the conic shape of rotating a vector or point along an axis.

3. Note that this axis is always throught the origin. An arbitrary rotation with an axis not going through the origin can be decomposed into a translation from a point on the axis to the origin, a rotation with an axis through the origin, and another translation back to the point.

4. The rotation angle and the rotation axis can be directly controlled by the three sliders. Note that to control the axis, alt-azimuth angles of the axis are used. Thus, even in the degenerated case, where the rotation angle is zero, the axis can still be defined using the alt-azimuth angles (the dotted line representing the projection of the axis on the ground is calculated by the azimuth angle, so even the axis is pointing to perpendicular to the ground, this dotted line is still defined and shown). The rotation angle is in [-180, +180] degrees, the alt angle is in [-90, +90] degrees, and the azimuth angle is in [-180, +180] degrees.

Demo of the Euler Angles Representation of a 3D Rotation

Explanations:

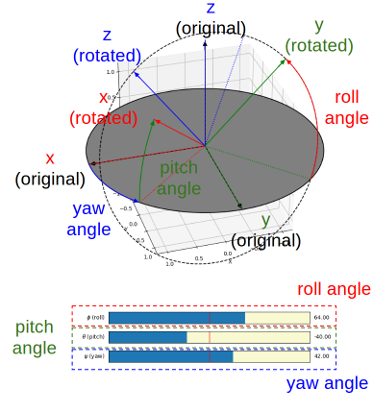
1. Yaw angle is shown as a blue arc on the ground, pointing from the x-axis of the original frame to the projection of the rotated x-axis on the ground.

2. Pitch angle is shown as a green arc, pointing from where the yaw angle arc ends to the rotated x-axis, i.e., from the tip of the projection of the rotated x-axis on the ground, which is shown as a dotted red line, to the tip of the rotated x-axis.

3. Roll angle is shown as a red arc in the rotated YOZ plane on a dashed circle, pointing from the tip of the projection of the rotated y-axis on the ground, which is shown as a dotted green line, to the tip of the rotated y-axis.

4. The projection of the z-axis of the original reference frame on the YOZ plane of the rotated reference frame is shown as a dotted blue line.

5. The three Euler angles can be directly controlled by the three sliders. All three angles are in [-180, +180] degrees. Even in the gimbal lock case, where the pitch angle is -90 degree or +90 degree, the yaw angle and the roll angle can be independently controlled, though their effects would be indistinguishable in this case.

Demo of the Rotation Matrix Representation of a 3D Rotation

Explanations:

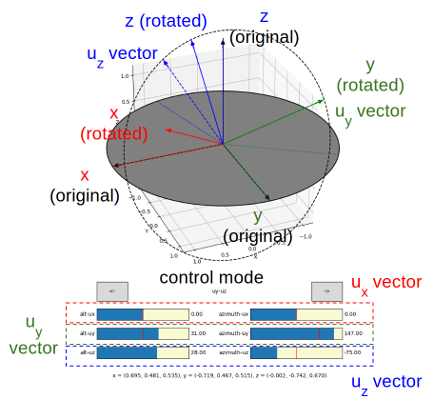
1. To construct a rotation matrix, three orthonormal basis vectors of the rotated reference frame are needed. However, since these three basis vectors are orthonormal, once two vectors are given (or one plane and a vector on the plane are given), the three basis vectors and the rotation matrix can be uniquely determined. This demo provides three modes as follows, and the current mode can be changed using the two buttons with "<-" and "->" arrows.

   1. "ux-uy", where the "ux" vector is the x-axis of the rotated reference frame, and "ux" and "uy" vectors together defines the XOY plane of the rotated reference frame. This plane is shown as a dashed circle. In this mode, "ux" is shown as a solid red line (i.e., the x-axis after rotation), and "uy" is shown as a dashed green line.

   2. "uy-uz", where "uy" vector is the y-axis of the rotated reference frame, and "uy" and "uz" vectors together defines the YOZ plane of the rotated reference frame. This plane is shown as a dashed circle. In this mode, "uy" is shown as a solid green line (i.e., the y-axis after rotation), and "uz" is shown as a dashed blue line.

   3. "uz-ux", where "uz" vector is the z-axis of the rotated reference frame, and "uz" and "ux" vectors together defines the ZOX plane of the rotated reference frame. This plane is shown as a dashed circle. In this mode, "uz" is shown as a solid blue line (i.e., the z-axis after rotation), and "ux" is shown as a dashed red line.

2. The three basis vectors of the rotated reference frame can be directly controlled using the sliders. Since they are all unit vectors (i.e., only the directions are important and their length do not matter), this demo program uses alt-azimuth angles to control them. In each mode, two vectors can be controlled and changing the third vector has no effect.

3. The projection of the two control vectors on the ground are shown as dotted lines with their corresponding colors. They are derived from the azimuth angles. The alt angles are in [-90, +90] degrees, and the azimuth angles are in [-180, +180] degrees.

Demo of the Unit Quaternion Representation of a 3D Rotation

Explanations:

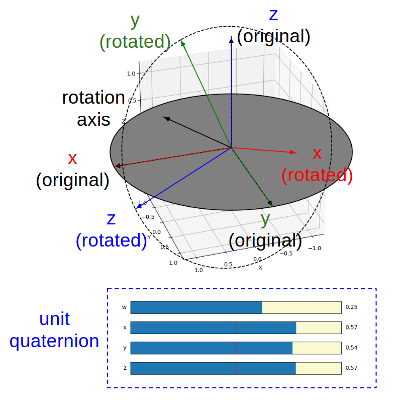
1. The rotation angle-axis, i.e., the vector u, corresponding to the unit quaternion is shown as a solid black arrow. The YOZ plane of the rotated reference frame is shown as a dashed circle.

2. The four components of the unit quaternion can be directly controlled by the four sliders. However, it is not straightforward to manuplate a quaternion to a rotation that the user desires. Since it is a unit quaternion, the four components are coupled and the user can not change one component without influence to others. This demo program provides three ways as follows.

   1. Changing the rotation angle while maintaining the axis, using the slider of qw. In this case, the other three components of the quaternion will be updated porpotionally to keep the direction of the rotation axis.

   2. Changing the axis direction while maintaining the angle (always to pi), by changing one of qx, qy, and qz. In this case, qw is always set to 0, while the the other two components not directly changed using the sliders are nonzero and updated propotionally. This allows the rotation axis, the axis changed by the sliders, as well as the corresponding axis of the original reference frame always stay in the same plane. For example, if the slider of qx is changed while qy and qz are nonzero, the rotation axis, the original x-axis, and the x-axis after rotation are in the same plane. The other two axes also keep this same coplaner property when the rotation axis is changed.

   3. Rotation along one of the axes of the original reference frame, by changing one of qx, qy, and qz. In this case, qw is always set to 0, while the other two components are also zero.

Usage of the pyrotation module

General Usage

First, import the pyrotation module.

>>> import pyrotation

For angle-axis, Euler angles, and rotation matrix, they use just built-in Python types and Numpy types, i.e., no custom class are defined. Hence, a set of function operating on built-in and numpy types are provided. For quaternion, a custome Quaternion class is defined and all operations on a quaternion are methods of the class or object.

Handling Singularity

This module defines a value EPSILON, which is considered as the precision required for floating point comparison (typically 1e-6). For example, if the absolute value of a floating point number a is less than EPSILON, a is considered as zero when handling singularity. In the following documentation, "if a is zero" generally means "if the absolute value of a is less than EPSILON" in the code.

Angle-Axis

• Use the alt_azimuth_to_axis(alt_degree, azimuth_degree) -> u function to create a unit vector u representing an axis from alt-azimuth angles in degrees. Note that the alt-azimuth angles are not restricted to be within a range. However, typically alt_degree should be in [-90, +90] degrees and azimuth_degree should be in [-180, +180] degrees.

• Use the axis_to_alt_azimuth(u) -> (alt_degree, azimuth_degree, gimbal_lock, degenerated) function to conver an axis vector u to alt-azimuth angles in degrees. If the length of u is zero, the degenerated flag is set to True, alt_degree is set to +90 degrees, and azimuth_degree is set to 0 degree. If u is nonzero but pointing to the z-axis or the opposite of the z-axis, the gimbal_lock flag is set to True, alt_degree is set to +90 degrees, and azimuth_degree is set to 0 degree.

• Use the rotate_a_point_by_angle_axis(p, u) -> rp function to rotate a point p by an angle-axis rotaion u and obtain the rotated point rp. Both p and rp are numpy 3-dimensional arrays.

• Use the rotate_points_by_angle_axis(ps, u) - rps function to rotate an array of points ps by an angle-axix rotation u and obtain the rotated array of points rps. Both ps and rps are numpy 3-by-n matrix where n is the number of points.

• Use the angle_axis_to_rotation_matrix(u) -> R function to convert an angle-axis u to a rotation matrix R. If the length of u is zero, the identity matrix is returned.

• Use the rotation_matrix_to_angle_axis(R) -> u function to convert a rotation matrix R to an angle-axis u. If R is the identity matrix, u is all zero, i.e., degenerated.

Euler Angles

• Use the euler_zyx_to_rotation_matrix(z, y, x) -> R function to convert the (yaw, pitch, roll) angles in radian to a rotation matrix R. The three angles are in this order: z-yaw, y-pitch, x-roll.

• Use the rotation_matrix_to_euler_angles_zyx(R) -> (z, y, x, gimbal_lock) function to convert a rotation matrix to the (yaw, pitch, roll) angles. If the rotation matrix represents a rotation corresponding to a pitch angle of -pi/2 degree or +pi/2 radian, i.e., R[2, 0] is +1 or -1, the gimbal_lock flag is set to True. In this case, roll angle is always set to 0.

Rotation Matrix

• Use the rotate_a_point_by_rotation_matrix(R, p) -> rp function to rotate a point p by a rotation matrix R and obtain the rotated point rp. Both p and rp are numpy 3-dimensional arrays.

• Use the rotate_points_by_rotation_matrix(R, ps) -> rps function to rotate an array of points ps by a rotation matrix R and obtain the rotated array of points rps. Both ps and rps are numpy 3-by-n matrix where n is the number of points.

• Use the normalize_rotation_matrix(R) -> Rn function to normalize a rotation matrix R to obtain a normalized matrix Rn. This function uses SVD.

• Use the rotation_matrix_from_orthonormal_basis(ux, uy, uz) -> R function to construct a rotation matrix R from three orthonormal basis vectors (ux, uy, uz).

• Use the orthonormal_basis_from_two_vectors(v1, v2, v1_default, v2_default) -> (u1, u2, u3) function to construct three orthonormal basis vectors (u1, u2, u3) from a pair of vector (v1, v2), where u1 is in the direction of v1, u2 is in the plane defined by v1 and v2, and u3 is orthogonal to the plane of v1 and v2. In the degenerated case 1, where v1 is all zero, v1_default is used instead. In the degenerated case 2, where v2 is all zero or v2 is in the same direction as v1, v2_default is used instead. There three helper functions based this one.

  • rotation_matrix_from_xy(x, y) -> R, i.e., constructing a rotation matrix R given two vectors representing the x-axis and the y-axis.
  • rotation_matrix_from_yz(y, z) -> R, i.e., constructing a rotation matrix R given two vectors representing the y-axis and the z-axis.
  • rotation_matrix_from_zx(z, x) -> R, i.e., constructing a rotation matrix R given two vectors representing the z-axis and the x-axis.

For these three helper functions, the first axis is always in the same direction of the first provided vector. If the second provided vector is not orthogonal to the vector, a vector on the plane defined by these two vectors that is orthogonal the first vector is constructed as the the second axis. The third axis is always perpendiculer to the plan defined by the two provided vectors. The reference frame is always right-handed.

Unit Quaternion

A unit quaternion is represented by an object of the class Quaternion defined in this module. The quaternion object is immutable after construction. All operations will return a new quaternion object instead of changing itself.

Some useful object methods are shown as follows.

• Use q.norm() -> n to get the norm of the quaternion q.

• Use q.conjugate() -> qc to get the conjugate of the quaternion q, i.e., if q is (w, x, y, z), qc is (w, -x, -y, -z).

• Use q.inverse() -> qi to get the inverse of the quaternion q.

• Use q.negate() -> qn to get the negate of the quaternion q, i.e., if q is (w, x, y, z), qn is (-w, -x, -y, -z).

• Use q1.multiply_quaternion(self, q2) -> q3 to get the composition of q1 and q2 as q3, i.e., q3 = q1 * q2, where "*" is quaternion multiplication. Note that q1 * q2 is generally not equal to q2 * q1.

For the following methods, q must be a unit quaternion and this method does not check that. If q is not a unit quaternion the results would be wrong.

• Use q.rotate_a_point(p) -> rp to rotate a point p by a unit quaternion q and obtain the rotated point rp. Both p and rp are numpy 3-dimensional arrays.

• Use q.rotate_points(ps) -> rps to rotate an array of points ps by a unit quaternion q and obtain the rotated array of points rps. Both ps and rps are numpy 3-by-n matrix where n is the number of points.

• Use q.to_angle_axis() -> u to convert a unit quaternion q to an angle-axis u.

• Use q.to_rotation_matrix() -> R to convert a unit quaternion q to a rotation matrix R.

Some useful class methods are shown as follows.

• Use Quaternion.identity() -> qi to construct the identity unit quaternion qi, i.e., (1, 0, 0, 0).

• Use Quaternion.construct_from_angle_axis(u) -> q to convert an angle-axis u to a unit quaternion q. In the degenerated case where u is all zero, the identity quaternion is returned.

• Use Quaternion.construct_from_rotation_matrix(R) -> q to convert a rotation matrix R to a unit quaternion q.

• Use Quaternion.interpolate(q0, q1, t) -> q to obtain a spherical linear interpolation (SLERP) of two unit quaternions q0 and q1 given a parameter t. If t is 0, q0 is returned, and if t is 1, q1 is returned. If t is between 0 and 1, a unit quaternion q representing a rotation continuously from the orientation q0 to the orientation q1 at the fraction t is returned.

More quaternion kinematics will be implemented in the future.