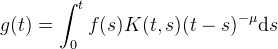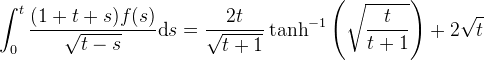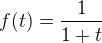This implements two methods for solving Volterra integral equations of the first kind,
These are integral equations for the function f where g and K are known functions. Note the t in the integration bounds. The factor (t-s)^{-\mu} accounts for any singularities in the kernel K. In other words, if you have an integral equation such that K(t,t) is unbounded (singular) and K(t,s) diverges like (t-s)^{-\mu} as t->s, rewrite it in the form above (so that K is well-behaved part of the origial kernel).
The methods used are based on [Linz, Ch. 10][1]. However, I have derived some of the formulas used here myself, since I had trouble implementing the formulas provided in the text. In any case, the spirit of the methods were inspired by the book.
The integral equation (taken from P. Linz, [Analytical and Numerical Methods for Volterra Equations][1])
has the exact solution
>>> import volterra
>>> def g(t):
... return 2*t*np.arctanh(np.sqrt(t/(t+1))) / np.sqrt(t+1) + 2*np.sqrt(t)
...
>>> def K(t,s):
... return 1 + t + s
...
>>> dt = 0.1
>>> t = np.arange(0.0, 100*dt, dt)
>>> F = volterra.block(K, g, dt, 100, mu=0.5)
>>> np.allclose(F, 1/(1+t), atol=1e-2, rtol=0.0)
True
>>> plot(t, F, '.')
>>> plot(t, 1/(1+t), 'k-')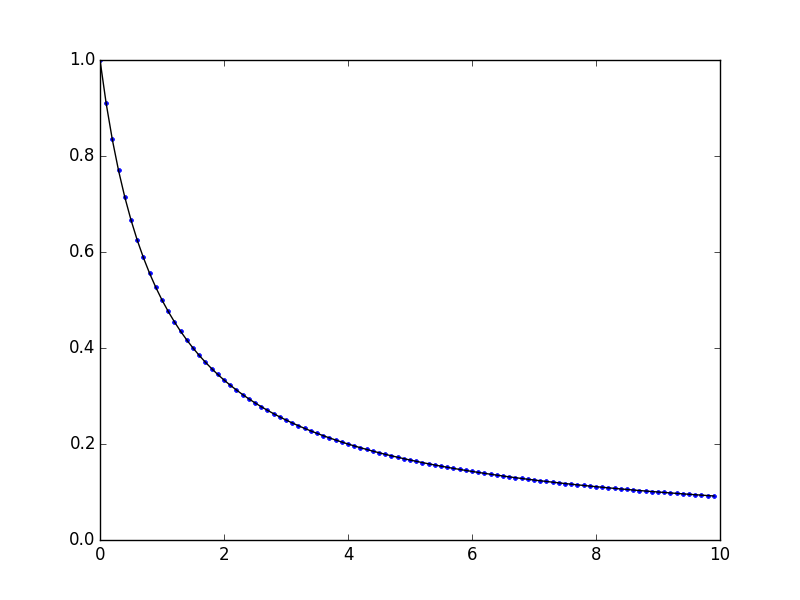 [1]: http://epubs.siam.org/doi/book/10.1137/1.9781611970852
[1]: http://epubs.siam.org/doi/book/10.1137/1.9781611970852
- At the moment, the solvers only work for
mu=0.5, but fixing this should be easy (I already have the needed formulas and it's just a matter of typing them out in Python) - The block method needs a value for
f(0)in order to start. You can supply a value with the optional argumentF0. If you don't provided a value,blockwill attempt to find a value, however it may choose poorly so beware!