[20211101] 제로베이스 알고리즘 자료구조 51일 대비반 DAY 17
junh0328 opened this issue · 0 comments
TodoList
- 전차시 복습
- 월요일 강의 듣기
-
퀴즈 풀이 및 제출
퀴즈 풀이 및 제출
이번 주는 자료구조 (배열,스택,큐,링크드리스트,해쉬테이블,트리)를 배웠는데, 정말 열심히 한다고 생각했지만 매우 매우 부족했다.
배열, 스택, 큐 에 대해서는 사전에 알고 있던 내용이라 크게 어려움을 느끼지 못했는데 이러한 마음 가짐으로 링크드 리스트, 해쉬 테이블, 트리에 들어가니 너무 너무 어려웠다.
모르는 부분을 3-4번 반복해서 들으며, 혼자 짜면서 복습을 하는 와중에도 해당 정보가 지식이 되어 내 머릿속으로 들어오는 느낌이 아니었다.
또한 이번 한 주를 내 스스로가 계획대로 제대로 통제하지 못하고 그냥 물 흘러가듯 흘려버린 주간인 것 같다.
알고리즘에 들어가기 전 내가 진짜 부족했다고 느꼈던 자료구조인 만큼 이번 주에는 자료구조 복습을 포함한 과제애 대한 해설을 바탕으로 조금 더 심도있게 다뤄봐야 할 것이다
2021.11.01, day 17
6.3. 빈번한 충돌을 개선하는 기법
- 해쉬 함수을 재정의 및 해쉬 테이블 저장공간을 확대
- 해쉬 테이블의 슬롯을 2배 이상으로 늘렸다
[0~15] - 예:
hash_table = list([None for i in range(16)])
def hash_function(key):
return key % 16참고: 해쉬 함수와 키 생성 함수
-
파이썬의 hash() 함수는 실행할 때마다, 값이 달라질 수 있음
-
값이 달라지지 않는 유명한 해쉬 함수들이 있음: SHA(Secure Hash Algorithm, 안전한 해시 알고리즘)
- 어떤 데이터도 유일한 고정된 크기의 고정값을 리턴해주므로, 해쉬 함수로 유용하게 활용 가능
7. 시간 복잡도
- 일반적인 경우(Collision이 없는 경우)는 O(1)
- 최악의 경우(Collision이 모두 발생하는 경우)는 O(n)
해쉬 테이블의 경우, 일반적인 경우를 기대하고 만들기 때문에, 시간 복잡도는 O(1) 🔥 이라고 말할 수 있음
8. 검색에서 해쉬 테이블의 사용 예
- 16개의 배열에 데이터를 저장하고, 검색할 때 O(n)
- 16개의 데이터 저장공간을 가진 위의 해쉬 테이블에 데이터를 저장하고, 검색할 때 O(1)
[자료구조] 트리
꼭 알아둬야 할 자료 구조: 트리 (Tree)
1. 트리 (Tree) 구조
-
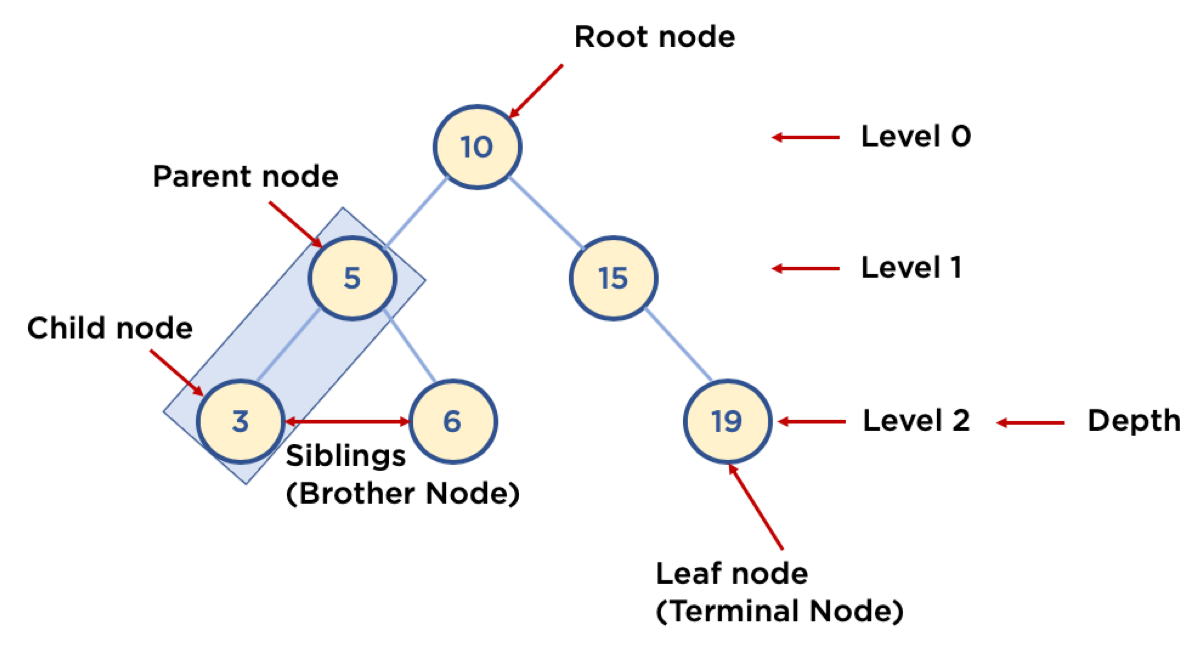
트리: 노드(node)와 브랜치(branch)를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
- 사이클은 아래 이미지를 기준으로 5 - 3 - 6 순으로 원을 그리며 탐색하는 것을 의미
- 트리 구조에서 Siblings 끼리는 브랜치로 이어지지 않는다 🔥
-
실제로 어디에 많이 사용되나?
- 트리 중 이진 트리 (Binary Tree)형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
- 트리 내부에 어떤 값을 가진 데이터가 존재하는지의 유무를 파악하기 쉽다
- 배열을 통해 배열의 길이만큼 전부 순회하는 것 보다 기준(left right)을 가지고 탐색하므로 더욱 빠르다
2. 알아둘 용어
- Node: 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
- Root Node: 트리 맨 위(최 상단)에 있는 노드
- Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 다음 레벨에 연결된 노드
- Child Node: 어떤 노드의 상위 레벨에 연결된 노드
- Leaf Node (Terminal Node): Child Node가 하나도 없는 노드
- Sibling (Brother Node): 동일한 Parent Node를 가진 노드
- Depth: 트리에서 Node가 가질 수 있는 최대 Level (깊이를 나타냄)
3. 이진 트리(Binary Tree)와 이진 탐색 트리(Binary Search Tree)
-
이진 트리: 노드의 최대 브랜치가 2개인 트리
- 이진 트리구조에서 워낙 이진 탐색 트리 형식으로 많이 쓰기 때문에
이진 트리 = 이진 탐색 트리라고 생각하는 경우도 있다 - 하지만 둘은 같지 않음
- 이진 트리는 루트 노드의 최대 브랜치가 2개인 트리이며, 사이클을 이루지 않도록 구성한 데이터 구조이지만,
- 이진 탐색 트리는 해당 이진 트리의 특징을 바탕으로 특정 조건을 붙인 트리이다
- 이진 트리구조에서 워낙 이진 탐색 트리 형식으로 많이 쓰기 때문에
-
이진 탐색 트리: 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음
4. 자료 구조 이진 탐색 트리의 장점과 주요 용도
- 주요 용도: 데이터 검색(탐색)
- 장점: 탐색 속도를 개선할 수 있음
단점은 이진 탐색 트리 알고리즘 이해 후에 살펴보기로 함
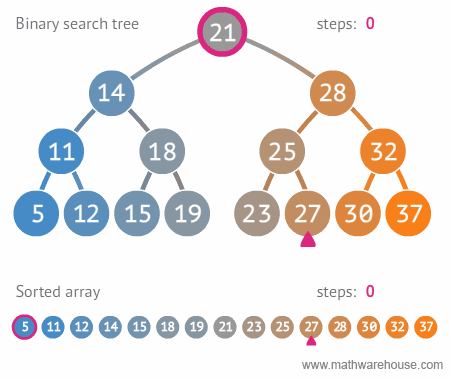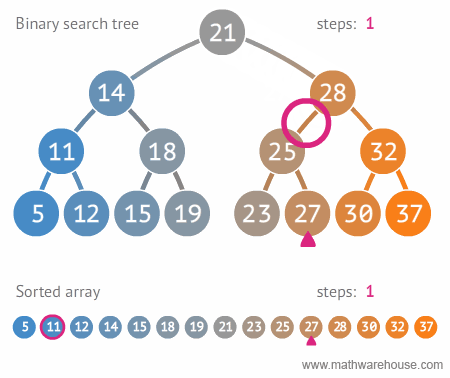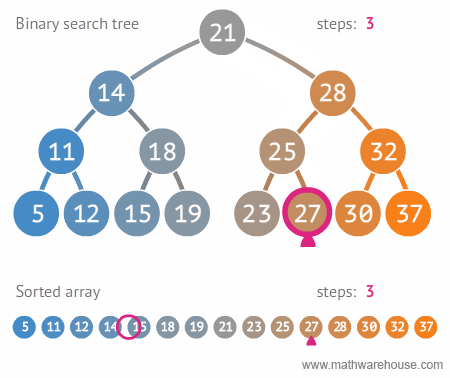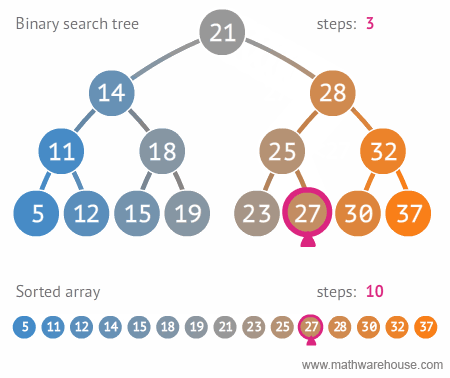
이진 트리와 정렬된 배열간의 탐색 비교 🔥
- steps: 단계의 가짓수를 보면 이진 트리가 훨씬 빠르게 검색을 할 수 있다
5. 파이썬 객체지향 프로그래밍으로 링크드 리스트 구현하기
주석 x
# 파이썬 객체지향 프로그래밍으로 링크드 리스트 구현하기
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class NodeManagement:
def __init__(self, head):
self.head = head
def insert(self, value):
self.current_node = self.head
while True:
if value < self.current_node.value:
if self.current_node.left != None:
self.current_node = self.current_node.left
else:
self.current_node.left = Node(value)
break
else:
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
def search(self, value):
self.current_node = self.head
while self.current_node:
if self.current_node.value == value:
print('find Value:', value)
return True
elif value < self.current_node.value:
print('go to left', value)
self.current_node = self.current_node.left
else:
print('go to right', value)
self.current_node = self.current_node.right
return False
head = Node(1)
BST = NodeManagement(head)
BST.insert(2)
BST.insert(3)
BST.insert(0)
BST.insert(4)
BST.insert(8)
print(BST.search(8))주석 o
# 주석 코드
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class NodeMgmt:
def __init__(self, head):
self.head = head
def insert(self, value):
self.current_node = self.head
while True:
# 입력한 value보다 사전에 초기화된 self.head의 value가 더 클 경우 (왼쪽으로 가야겠죠?)
if value < self.current_node.value:
# 왼쪽으로 갔는데, self.head의 오른쪽에 데이터가 있다면 (None이 아니라면)?
if self.current_node.left != None:
self.current_node = self.current_node.left
# 왼쪽으로 갔는데, self.head의 오른쪽에 데이터가 없다면 (Nonde 이라면)?
else:
self.current_node.left = Node(value)
break
# 입력한 value가 self.head.value보다 클 경우 (오른쪽으로 가야겠죠?)
# 같을 경우에도 오른쪽으로 가게 처리했다
else:
if self.current_node.right != None:
# self.current_node(=self.head) 헤드를 self.current_node.right로 바꿔줘라
self.current_node = self.current_node.right
else:
# right에 새로운 Node(value)를 붙여주고 종료해라
self.current_node.right = Node(value)
break
# ---- insert까지는 위와 동일한 코드이다 ----
# 데이터의 여부를 파악하기 때문에, True <-> False를 반환한다
def search(self, value):
# self.current_node 라는 변수를 통해 self.head를 할당한 후 어디서부터 순회할지 결정한다
# 순회할 기준은 처음 head로 설정한 값이겠죠?
self.current_node = self.head
while self.current_node:
# 현재 self.current_node의 value가 내가 찾고자하는 value라면 True를 반환한다
if self.current_node.value == value:
print('find value:', value)
return True
# 내가 찾고자하는 value가 self.current_node의 value보다 작을 경우 (왼쪽)
elif value < self.current_node.value:
print('go to left')
self.current_node = self.current_node.left
# 내가 찾고자하는 value가 self.current_node의 value보다 클 경우 (오른쪽)
else:
# 같을 경우도 오른쪽으로 이동한다
print('go to right')
self.current_node = self.current_node.right
# 순회했을 때 없을 경우에는 False를 반환한다
return False
head = Node(1)
BST = NodeMgmt(head)
print('head.value:', BST.head.value)
BST.insert(2)
BST.insert(3)
BST.insert(0)
BST.insert(4)
BST.insert(8)
print(BST.search(8))