Lemma odd-even sort in lecture notes

[HaritzPuerto]

Hello,
I do not know how to prove this lemma and I do not understand it either.

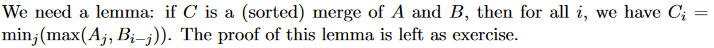
Let's suppose A = [2,5] and B = [1,6]
merge (A,B) = [1,2,5,6]

According to the lemma, Ci = minj(max(Aj, Bi-j)), so for all combinations of i and j, we want the one with the lowest j, right? minj means argmin j, doesn't it?

Then
C[0] = minj(max(A[0], B[0]) = 2 (note i = j = 0) but this is wrong! It should be 1, so should it be min instead of max?
C[1] = minj( {max(A[0], B[1-0]), max(A[1], B[0]) }) = minj( 6, 1) = 6 (because j = 0, in the other option j =1) but again this is wrong, it should be 2. If I use min instad of max, I would have minj(2, 1) = 2

Can someone explain to me what I am doing wrong and how to prove the lemma?
Thank you

[jeehoonkang]

• Let's assume the index begins from 1, and A[0] = B[0] = minus infinity.
• Then C[1] = min_j (max(A_j, B_(1-j))) = min(B[1], A[1]).

[HaritzPuerto]

Thank you!