五子棋AI教程第二版四:Alpha-Beta 剪枝
lihongxun945 opened this issue · 10 comments
剪枝是必须的
上一篇讲了极小化极大值搜索,其实单纯的极小化极大值搜索算法并没有实际意义。
可以做一个简单的计算,平均一步考虑 50 种可能性的话,思考到第四层,那么搜索的节点数就是 50^4 = 6250000,在我的酷睿I7的电脑上一秒钟能计算的节点不超过 5W 个,那么 625W 个节点需要的时间在 100 秒以上。电脑一步思考 100秒肯定是不能接受的,实际上最好一步能控制在 5 秒 以内。
顺便说一下层数的问题,首先思考层数必须是偶数。因为奇数节点是AI,偶数节点是玩家,如果AI下一个子不考虑玩家防守一下,那么这个估分明显是有问题的。
然后,至少需要进行4层思考,如果连4四层都考虑不到,那就是只看眼前利益,那么棋力会非常非常弱。 如果能进行6层思考基本可以达到对战普通玩家有较高胜率的水平了(普通玩家是指没有专门研究过五子棋的玩家,棋力大约是4层的水平),如果能达到8层或以上的搜索,对普通玩家就有碾压的优势,可以做到90%以上胜率。
Alpha Beta 剪枝原理
Alpha Beta 剪枝算法是一种安全的剪枝策略,也就是不会对棋力产生任何负面影响。它的基本依据是:棋手不会做出对自己不利的选择。依据这个前提,如果一个节点明显是不利于自己的节点,那么就可以直接剪掉这个节点。
前面讲到过,AI会在MAX层选择最大节点,而玩家会在MIN层选择最小节点。那么如下两种情况就是分别对双方不利的选择:
- 在MAX层,假设当前层已经搜索到一个最大值 X, 如果发现下一个节点的下一层(也就是MIN层)会产生一个比X还小的值,那么就直接剪掉此节点。
解释一下,也就是在MAX层的时候会把当前层已经搜索到的最大值X存起来,如果下一个节点的下一层会产生一个比X还小的值Y,那么之前说过玩家总是会选择最小值的。也就是说这个节点玩家的分数不会超过Y,那么这个节点显然没有必要进行计算了。
通俗点来讲就是,AI发现这一步是对玩家更有利的,那么当然不会走这一步。
- 在MIN层,假设当前层已经搜索到一个最小值 Y, 如果发现下一个节点的下一层(也就是MAX层)会产生一个比Y还大的值,那么就直接剪掉此节点。
这个是一样的道理,如果玩家走了一步棋发现其实对AI更有利,玩家必定不会走这一步。
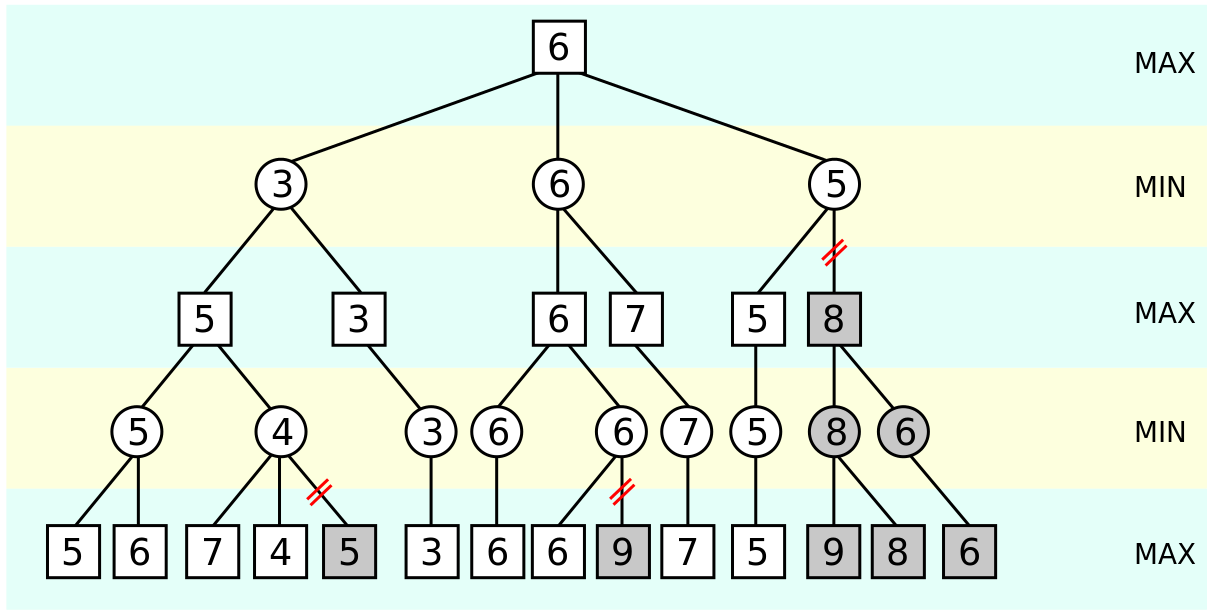
下面图解说明,直接用wiki上的图:
如上图所示,在第二层,也就是MIN层,当计算到第二层第三个节点的时候,已知前面有一个3和一个6,最大值至少是6。 在计算第三个节点的时候,发现它的第一个孩子的结果是5,因为当前是MIN节点,会选择孩子中的最小值,所以此节点值不会大于5。而第二层已经有一个6了,第二层第三个节点肯定不会被选择。因此此节点的后序孩子就没有必要计算了。
其实这个图里面第三层分数为7的节点也是不需要计算的。
这是 MAX 节点的剪枝,MIN节点的剪枝也是同样的道理,就不再讲了。 Alpha Beta 剪枝的 Alpha 和 Beta 分别指的是MAX 和 MIN节点。
代码实现
虽然原理说了很多,但是其实代码的实现特别简单。
对max和min函数都增加一个 alpha 和 beta 参数。在 max 函数中如果发现一个子节点的值大于 alpha,则不再计算后序节点,此为 Alpha 剪枝。在 min 函数中如果发现一个子节点的值小于 beta,则不再计算后序节点,此为 Beta剪枝。
代码实现如下:
var r = function(deep, alpha, beta, role, step, steps, spread) {
var _e = board.evaluate(role)
var leaf = {
score: _e,
step: step,
steps: steps
}
return leaf
}
var best = {
score: MIN,
step: step,
steps: steps
}
// 双方个下两个子之后,开启star spread 模式
var points = board.gen(role, step > 1, step > 1)
if (!points.length) return leaf
for(var i=0;i<points.length;i++) {
var p = points[i]
board.put(p, role)
var _deep = deep-1
var _spread = spread
var _steps = steps.slice(0)
_steps.push(p)
var v = r(_deep, -beta, -alpha, R.reverse(role), step+1, _steps, _spread)
v.score *= -1
board.remove(p)
// 注意,这里决定了剪枝时使用的值必须比MAX小
if(v.score > best.score) {
best = v
}
alpha = Math.max(best.score, alpha)
//AB 剪枝
if(math.greatOrEqualThan(v.score, beta)) {
// AB 剪枝,不用进行接下来的遍历了,直接返回
return v
}
}
return best
}优化效果
按照wiki上的说法,最大优化效果应该达到 1/2 次方。也就是如果你本来需要计算 10000 个节点,那么最好的效果是,你只需要计算 100 个点就够了。这是建立在所有的节点排序都是完美的假设上的。因为我们不可能完美排序,所以我们的优化效果达不到那么好。但是依然可以达到约 3/4次方 的优化效果。
对生成的着法进行排序的算法,就叫 启发式评估函数,下一章我们介绍如何实现启发式评估函数。
在MIN层,假设当前层已经搜索到一个最小值 Y, 如果发现下一个节点的下一层(也就是MIN层)会产生一个比Y还大的值,那么就直接剪掉此节点。
应该改为
在MIN层,假设当前层已经搜索到一个最小值 Y, 如果发现下一个节点的下一层( #也就是MAX层)会产生一个比Y还大的值,那么就直接剪掉此节点。
@gongym12138 感谢 已更正
在剪枝中的r函数中,(negamax.js的191行),注释里写有“这里必须是 greatThan 即 明显大于,而不是 greatOrEqualThan”,但是下一行调用了greatOrEqualThan,请问这里?
请问,在这个算法中alpha有可能比beta小吗
其实这个图里面第三层分数为7的节点也是不需要计算的。
7的上层为MIN层,兄弟节点有6了确实不会被采用,但是dfs算法当你知道这个节点的值为7的时候说明7的子树已经全部遍历完了啊.运算量已经消耗了.
剪枝只可能剪去非叶子节点吧 图中把叶子节点都剪掉了
我有一点疑惑,剪枝的分数需要回溯才能得到,示例的剪枝是遍历到第4层开始剪枝,然后剪枝后继续遍历,这样的剪枝虽然有一定合理性,但是不是就是伪剪枝呢。或者我理解错了?
感觉图好像确实有点问题,最右边不可能在到达叶子节点之前就全部剪掉
感觉图好像确实有点问题,最右边不可能在到达叶子节点之前就全部剪掉
应该是剪掉下面两个6
在剪枝中的r函数中,(negamax.js的191行),注释里写有“这里必须是 greatThan 即 明显大于,而不是 greatOrEqualThan”,但是下一行调用了greatOrEqualThan,请问这里?
我也觉得奇怪hh,而且我看源码里面也是写的greatOrEqualThan,其实alpha beta剪枝就是alpha>=beta,所以应该就是这么写没问题