MATLAB Code for Topology Optimization of Plates
This is a project developed by a small group of students of the Civil Engineering Master Degree at the University of Trento (Italy) for the Computational Mechanics of Structures 2 course.
The aim is to explore the topology optimization area by embedding its techniques into a structural application. In particular, we focused on two problems of constrained optimization:
- Finding the mass distribution on a plate which minimizes its compliance (work of loads), given a fixed amount of material;
- Finding the mass distribution on a plate which maximizes a specified eigenfrequency, given a fixed amount of material.
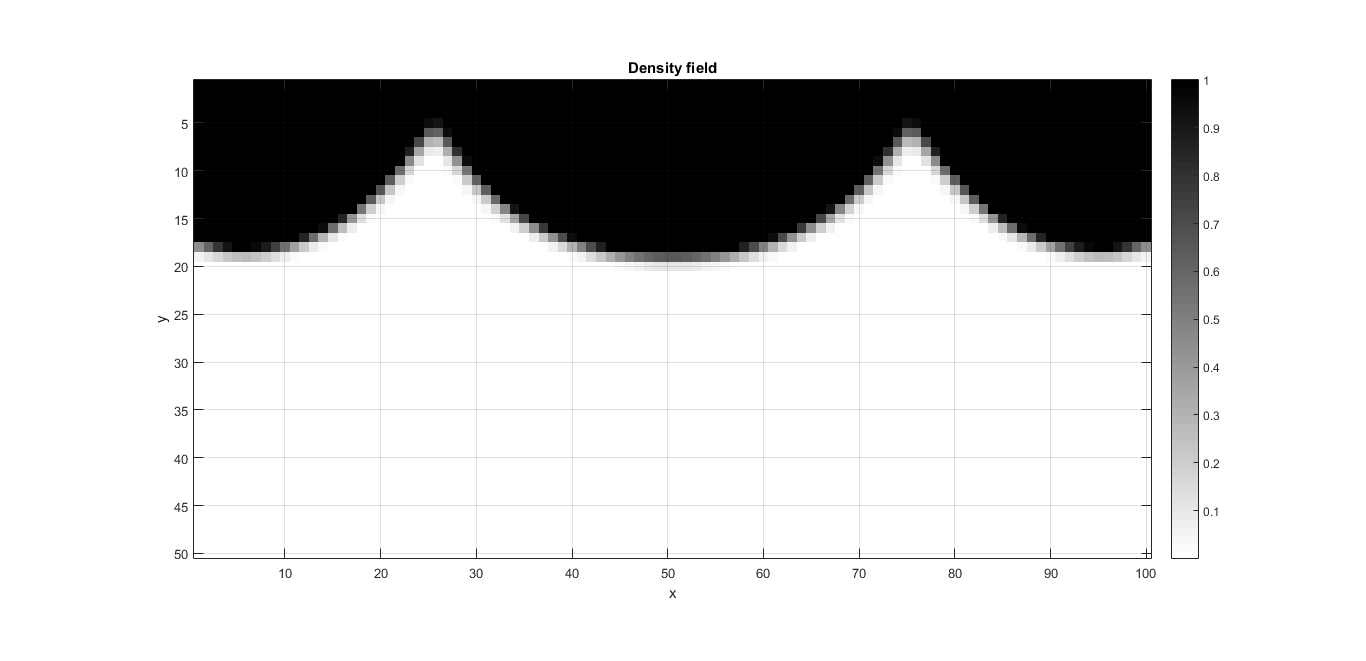
A discretization of the domain (plate) is performed and the SIMP (Solid Isotropic Material with Penalization) model is used to formulate these problems. Then, applying the FEM (Finite Element Method) and the OC (Optimality Criteria) method, the code implements the optimization procedure to find the optimal material density field.
The main functionalities implemented in the code are
- Compliance Optimization (work of loads minimization)
- Eigenfrequencies Optimization
- Different types of finite element available (ACM, BMF, etc.)
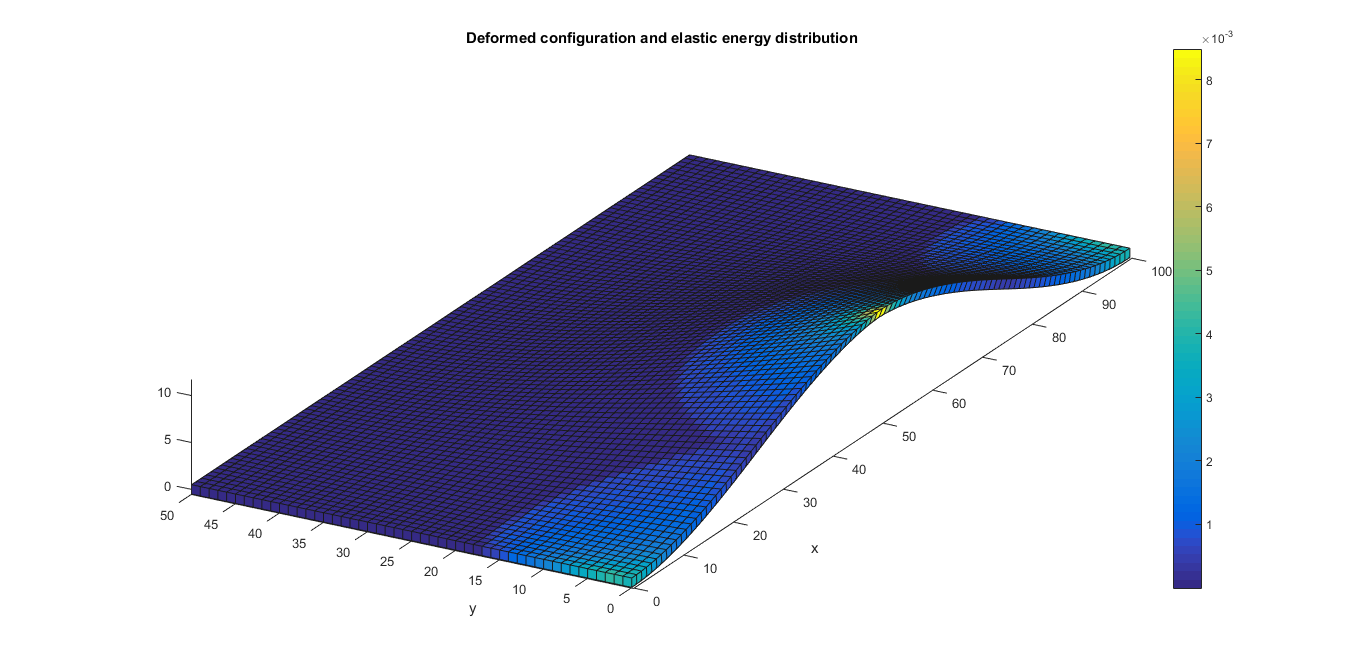
- Plots displaying convergence, optimal design, deformed configuration and eigenmodes
Basically you just need to run one of the two main files (main_compliance.m or main_eigenfrequncies.m) and see what happens 😄.
As you can see, in the main files there are several parameters to set as you want, such as plate dimensions, material properties, volume contraint as well as the type of finite element to use in the computation.
Obviously you can modify the code as you want. For example, if you'd like to change the problem to be solved, just set the problemId in the main file to match a value of the available cases defined in the Problem class. And if you want to start to get your hands dirty with the code, you can create your own cases in this class, so that you can solve whatever problem you like 😎.
Possibly some of these areas may be explored and developed in the future
- Multiobjective Optimization (for compliance problems)
- Band Gap Optimization
- Performance improvements through numerical integration
- Other optimization methods such as the Method of Moving Asymptotes (MMA)
Here's a brief list of the main papers used to explore the field.
- Sergey Ananiev (2003) - On Equivalence between Optimality Criteria and Projected Gradient Methods with Application to Topology Optimization Problem
- Matteo Bruggi, Alberto Taliercio (2014) - Optimal strengthening of concrete plates with unidirectional fiber-reinforcing layers
- Jianbin Du, Niels Olhoff (2005) - Topology optimization of continuum structures with respect to simple and multiple eigenfrequencies
- Ole Sigmund (2006) - Morphology-based black and white filters for topology optimization
- Zhen-Gong Ma, Noboru Kikuchi, Hsien-Chie Cheng (1994) - Topological design for vibrating structures
- Jianbin Du, Niels Olhoff (2005) - Topological design of freely vibrating continuum structures for maximum values of simple and multiple eigenfrequencies and frequency gaps
- Erik Lund, Niels Olhoff (1994) - Multiple eigenvalues in structural optimization problems
- Krister Svanberg (1987) - The Method of Moving Asymptotes