This code is in prob.py.
A finite random variable is specified by a probability mass function (PMF):
class RV(object):
def __init__(self,pmf):
self._pmf = pmf
def pmf(self,x):
if x in self._pmf:
return self._pmf[x]
else:
return 0
def range(self):
return self._pmf.keys()Entropy is a function of a random variable:
def H(X):
p = X.pmf
return sum(-p(x) * log2(p(x)) for x in X.range() if p(x) > 0)Here are some examples:
In [1]: X = RV({0:0.5,1:0.5})
In [2]: H(X)
Out[2]: 1.0
In [3]: Y = RV({0:0.1,1:0.9})
In [4]: H(Y)
Out[4]: 0.46899559358928122
In [5]: Z = RV({'a':0.5,'b':0.25,'c':0.125,'d':0.125})
In [6]: H(Z)
Out[6]: 1.75
In [7]: W = RV({'a':0,'b':0,'c':1})
In [8]: H(W)
Out[8]: 0.0A special binary random variable class can provide a convenient constructor:
class BinaryRV(RV):
def __init__(self,p):
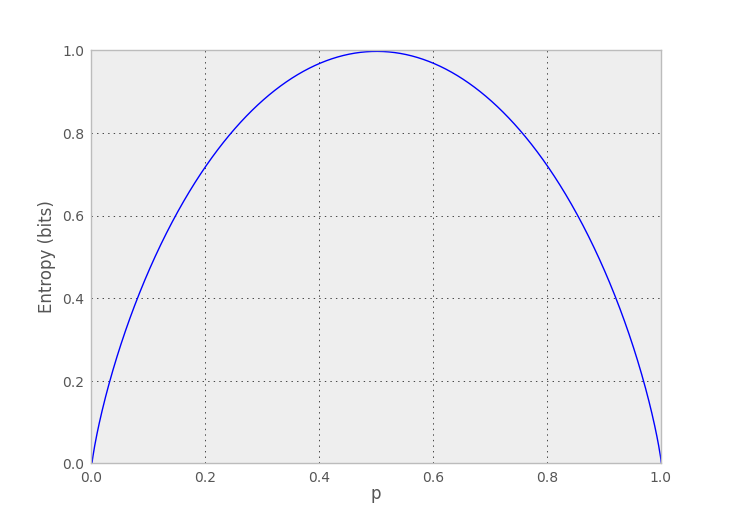
super(BinaryRV,self).__init__({0:1-p,1:p})In [1]: ps = np.linspace(0,1,1000)
In [2]: plt.plot(ps,[H(BinaryRV(p)) for p in ps])
In [3]: plt.xlabel('p')
In [4]: plt.ylabel('Entropy (bits)')This code is also in prob.py.
A discrete-time stochastic process is just a sequence of (possibly dependent) random variables, one for each time step. A useful process object will be able to generate a random sequence and also report its entropy rate.
class Process(object):
__metaclass__ = abc.ABCMeta
def sample_sequence(self,N):
return ''.join(islice(self.sequence_generator(),N))
@abc.abstractmethod
def sequence_generator(self):
pass
@abc.abstractmethod
def H_rate(self):
pass
def H_rate(process):
return process.H_rate()A simple process is just a sequence of independent and identically distributed (IID) random variables. An entropy rate for an IID process is just the entropy of its underlying random variable:
class IIDProcess(Process):
def __init__(self,pmf):
self._rv = RV(pmf)
def sequence_generator(self):
X = self._rv
while True:
yield sample(X.range(),p=X._pmf.values())
def H_rate(self):
return H(self._rv)In [1]: X = IIDProcess({'a':0.2,'b':0.8})
In [2]: X.sample_sequence(20)
Out[2]: 'bbbbaabbbbbbbbabbbbb'
In [3]: X.sample_sequence(50)
Out[3]: 'bbbbbabbbbbbabbbbbbbbbbbabbbbbabbbbbabbbbbbbbbabbb'
In [4]: H_rate(X)
Out[4]: 0.72192809488736231
In [5]: H_rate(IIDProcess({0:0.5,1:0.5}))
Out[5]: 1.0A slightly more interesting process is a Markov process, where the probability
of a symbol depends on the previous symbol, so there's a transition matrix P
where P[i,j] is the probability of going to the symbol at index j from the
symbol at index i.
class MarkovProcess(Process):
def __init__(self,symbols,trans):
self._symbols = symbols
self._numstates = len(symbols)
self._P = np.asarray(trans)
self._pi = util.steady_state(self._P)
def sequence_generator(self):
state = sample(self._numstates,p=self._pi)
while True:
yield self._symbols[state]
state = sample(self._numstates,p=self._P[state])
def H_rate(self):
P = self._P
PlogP = P*log2(np.where(P != 0, P, 1))
return -self._pi.dot(PlogP).sum()In [1]: process = MarkovProcess(('a','b','c','d'),
....: np.array([[0.9,0.1, 0, 0],
....: [0.1,0.8,0.1, 0],
....: [ 0,0.1,0.8,0.1],
....: [ 0, 0,0.1,0.9]]))
In [2]: process.sample_sequence(50)
Out[2]: 'aaaaaaaaaaaaaaaaaaaaaabbbbbcccccccccccccdddddddddd'
In [3]: process.sample_sequence(75)
Out[3]: 'aaaaaaaaabbccccccddddcccccbbbbbbbbbbbaaabbbcccbbaaaaaaaaaaaaaaaaaaaaabbcccc'
In [4]: H_rate(process)
Out[4]: 0.69546184423832147That Markov chain is so predictable that its entropy rate is less than a single bit per symbol, even though there are 4 possible symbols.
This code is in compress.py.
If we have a probabilistic model for a process then we can design a good code for it, where "good" means "short codeword lengths on average". The entropy rate of the process gives a lower bound on the average codeword length.
For an IID process, we just need a probabilistic model for its underlying random variable (i.e. an estimate of the underlying PMF), and the entropy rate is just the entropy of that random variable. Given such a model, there is a simple greedy algorithm that yields an optimal prefix code (asymptotically with long block lengths); it's called the Huffman algorithm.
def huffman(X):
p = X.pmf
# make a queue of symbols that we'll group together as we build the tree
queue = [(p(x),(x,)) for x in X.range()]
heapify(queue)
# the initial codes are all empty
codes = {x:'' for x in X.range()}
while len(queue) > 1:
# take the two lowest probability (grouped) symbols
p1, symbols1 = heappop(queue)
p2, symbols2 = heappop(queue)
# add a bit to each symbol group's codes
for s in symbols1:
codes[s] = '0' + codes[s]
for s in symbols2:
codes[s] = '1' + codes[s]
# merge the two groups and push them back to the queue
heappush(queue, (p1+p2, symbols1+symbols2))
# return them ordered by code length
return OrderedDict(sorted(codes.items(),key=lambda x: len(x[1])))In [1]: X = RV({'a':0.5,'b':0.25,'c':0.125,'d':0.125})
In [2]: huffman(X)
Out[2]: OrderedDict([('a', '0'), ('b', '10'), ('c', '110'), ('d', '111')])
In [3]: codebook = huffman(X)
In [4]: p = X.pmf
In [5]: sum(p(x)*len(code) for x,code in codebook.items())
Out[5]: 1.75
In [6]: H(X)
Out[6]: 1.75More generally, a code is something that can compress and decompress, and a model-based code gives a way to construct a code based on fitting a probabilistic model to the data to be compressed:
class Code(object):
__metaclass__ = abc.ABCMeta
@abc.abstractmethod
def compress(self,seq):
pass
@abc.abstractmethod
def decompress(self,bitstring):
pass
class ModelBasedCode(Code):
__metaclass__ = abc.ABCMeta
@classmethod
@abc.abstractmethod
def fit(cls,seq,blocklen=1):
pass
class IIDCode(ModelBasedCode):
def __init__(self,codebook):
self.codebook = codebook
self.inv_codebook = {v:k for k,v in codebook.iteritems()}
def compress(self,seq):
for s in seq:
yield self.codebook[s]
def decompress(self,bits):
bits = iter(bits)
while True:
yield self.consume_next(self.inv_codebook,bits)
@staticmethod
def consume_next(inv_codebook,bits):
# NOTE: prefix-free is important here!
bitbuf = ''
for bit in bits:
bitbuf += bit
if bitbuf in inv_codebook:
return inv_codebook[bitbuf]
assert len(bitbuf) == 0
raise StopIteration
def __repr__(self):
return self.__class__.__name__ + '\n' + \
'\n'.join('%s -> %s' % (symbol, code)
for symbol, code in self.codebook.iteritems())
@classmethod
def fit(cls,seq):
model = cls.estimate_iid_source(seq)
return cls.from_rv(model)
@classmethod
def from_rv(cls,X):
return cls(huffman(X))
@staticmethod
def estimate_iid_source(seq):
counts = defaultdict(int)
tot = 0
for symbol in seq:
counts[symbol] += 1
tot += 1
pmf = {symbol:count/tot for symbol, count in counts.iteritems()}
return RV(pmf)In [1]: true_process = IIDProcess({'a':0.6,'b':0.2,'c':0.1,'d':0.1})
In [2]: H_rate(true_process)
Out[2]: 1.5709505944546687
In [3]: seq = true_process.sample_sequence(20000)
In [4]: IIDCode.fit(seq)
Out[4]:
IIDCode
a -> 1
b -> 00
c -> 011
d -> 010
In [5]: ''.join(IIDCode.fit(seq).compress(seq))[:50]
Out[5]: '11110000100001101111101001111110011110011110100101'
In [6]: IIDCode.fit_and_compress(seq) # convenience method with a report
IIDCode
a -> 1
b -> 00
c -> 011
d -> 010
IIDCode with block length 1 achieved compression rate: 0.80435x
(2 bits per raw symbol, 1.6087 compressed bits per symbol)We can do something similar with Markov processes by creating a Huffman code for each symbol (that is, for each row of the transition matrix):
class MarkovCode(ModelBasedCode):
def __init__(self,firstcodebook,codebooks):
self.firstcode = IIDCode(firstcodebook)
self.iid_codes = {symbol:IIDCode(codebook)
for symbol, codebook in codebooks.iteritems()}
def compress(self,seq):
s1, s2 = tee(seq,2)
firstsymbol = next(s2)
yield self.firstcode.codebook[firstsymbol]
for a,b in izip(s1,s2):
yield self.iid_codes[a].codebook[b]
def decompress(self,bits):
bits = iter(bits)
symbol = IIDCode.consume_next(self.firstcode.inv_codebook,bits)
while True:
yield symbol
symbol = IIDCode.consume_next(self.iid_codes[symbol].inv_codebook,bits)
def __repr__(self):
return self.__class__.__name__ + '\n' + \
'\n'.join('Code after seeing %s:\n%s' % (symbol,iidcode)
for symbol, iidcode in self.iid_codes.iteritems())
@classmethod
def fit(cls,seq):
model = cls.estimate_markov_source(seq)
return cls.from_markovchain(model)
@classmethod
def from_markovchain(cls,(symbols,pi,P)):
return cls(huffman(RV(dict(zip(symbols,pi)))),
{s:huffman(RV(dict(zip(symbols,dist))))
for s,dist in zip(symbols,P)})
@staticmethod
def estimate_markov_source(seq):
s1, s2 = tee(seq,2)
next(s2)
counts = defaultdict(lambda: defaultdict(int))
tots = defaultdict(int)
for a,b in izip(s1,s2):
counts[a][b] += 1
tots[a] += 1
symbols = counts.keys()
P = np.array([[counts[i][j]/tots[i] for j in symbols] for i in symbols])
pi = util.steady_state(P)
return (symbols, pi, P)In [1]: process = MarkovProcess(('a','b','c','d'),
....: np.array([[0.9,0.1, 0, 0],
....: [0.1,0.8,0.1, 0],
....: [ 0,0.1,0.8,0.1],
....: [ 0, 0,0.1,0.9]]))
In [2]: H_rate(process)
Out[2]: 0.695462
In [3]: seq = process.sample_sequence(20000)
In [4]: IIDCode.fit_and_compress(seq)
IIDCode
a -> 01
c -> 10
b -> 00
d -> 11
IIDCode with block length 1 achieved compression rate: 1x
(2 bits per raw symbol, 2 compressed bits per symbol)
In [5]: IIDCode.fit_and_compress(seq,blocklen=2)
IIDCode
aa -> 01
cc -> 00
dd -> 10
bb -> 111
bc -> 11001
cd -> 11000
ab -> 110100
ba -> 110101
cb -> 110111
dc -> 110110
IIDCode with block length 2 achieved compression rate: 0.683725x
(4 bits per raw symbol, 2.7349 compressed bits per symbol)
In [6]: MarkovCode.fit_and_compress(seq)
MarkovCode
Code after seeing a:
IIDCode
a -> 1
b -> 01
c -> 000
d -> 001
Code after seeing c:
IIDCode
c -> 1
b -> 01
a -> 000
d -> 001
Code after seeing b:
IIDCode
b -> 1
c -> 01
a -> 001
d -> 000
Code after seeing d:
IIDCode
d -> 1
c -> 01
a -> 000
b -> 001
MarkovCode with block length 1 achieved compression rate: 0.59775x
(2 bits per raw symbol, 1.1955 compressed bits per symbol)This code is also in compress.py.
TODO Lempel-Ziv