A class library for using conformal geometric algebra in C#
A lot of operators are overloaded so that you can write your calculations in C# source code almost like you would do in a math software. But please be aware that I didn't have enough time to fully understand how the theory of geometric algebra really works. I just had an exciting time by implementing all the operators in C# so that it becomes easy to play with those calculations. This means that there is ABSOLUTELY NO WARRANTY that the calculations are correct and you should expect bugs in this library (it is not tested)!
Here are some useful links to get an idea about the theory and the uses of geometric algebra:
- http://www.researchgate.net/publication/228955605_A_brief_introduction_to_Clifford_algebra
- http://www.wolftype.com/versor/colapinto_masters_final_02.pdf
- http://tuprints.ulb.tu-darmstadt.de/epda/000764/DissertationDH061213.pdf
This project was originally created on SourceForge in the context of a optional module during my studies. Since I'd like to have my projects in one place I moved this project to GitHub. I also did some tweaks so that the visualization and the example application works on Linux with Mono.
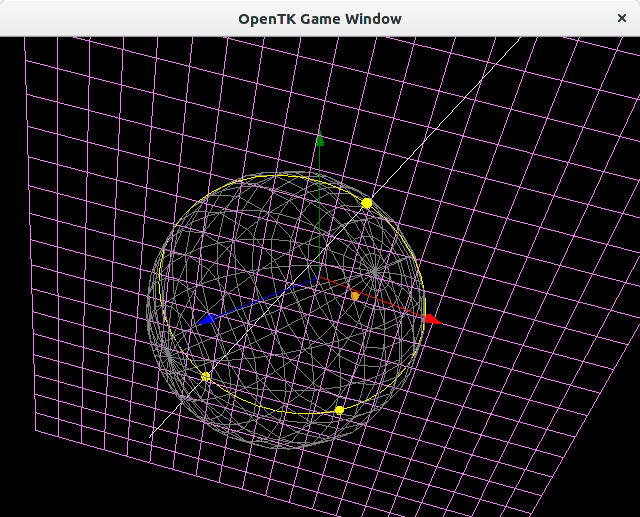
Currently there is no documentation of the library. Have a look at the sample application to get an idea of how everything works. Additionally I put some illustrative code below which shows some example calculations using geometric algebra with AlgeoSharp.
// Create some points
var p1 = IPNS.CreatePoint(2, 3, 0);
var p2 = IPNS.CreatePoint(-3, -4, 3);
var p3 = IPNS.CreatePoint(1, -5, 0);
var p4 = IPNS.CreatePoint(-1, -2, -3);
// Calculate the sphere described by all four points
var s = (p1 ^ p2 ^ p3 ^ p4).Dual;
// Calculate the plane described by three points
var p = (p1 ^ p2 ^ p3 ^ Basis.E8).Dual;
// Calculate the intersection between the plane and the sphere ...
var i = s ^ p;
// ... this should give us a circle which could also be obtained
// by using the three points
var c = (p1 ^ p2 ^ p3).Dual;In order to visualize the results there is a helper library AlgeoSharp.Visualization. This library uses OpenTK to display the MultiVectors in a window (see sample application), so make sure you have OpenTK installed on your system.