图解拼多多&leetcode14:最长公共前缀
sisterAn opened this issue · 20 comments
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入: ["flower","flow","flight"]
输出: "fl"示例 2:
输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。附leetcode:leetcode
场景案例【网易】:
有一个场景,在一个输入框输入内容,怎么更加高效的去提示用户你输入的信息,举个例子,你输入天猫,那么对应的提示信息是天猫商城,天猫集团,这个信息如何最快的获取,有没有不需要发请求的方式来实现?
提示:
- 数据请求:防抖、节流
- 数据存储处理:Trie树
大致思路:
- 新建一个变量 result 用于存储重叠部分
- 对传入数组进行遍历
- 第一次遍历时变量 result 即为第一个元素
- 之后每次遍历都找出开头重叠部分,重叠部分只能保持不变或变少,当有一次为空时停止遍历 (arr.some())
比较字符串方法:
- 将字符串转换为数组
- 通过字符串下标进行比较
function overlap(arr) {
var result = '';
var firstTime = true;
arr.some(function (item) {
if( typeof item !== 'string') return false;
if( firstTime ) { // 考虑了数组第一个元素可能不是字符串的情况
result = item;
firstTime = false;
return false; // 第一次填充字符串的话后面的代码就不用执行了
}
// 筛选出当前遍历字符串与 result 的交集
result = filterString(result, item);
// 每次遍历后都判断当前重叠部分是否为空,若为空直接返回
if( !result ) return true;
})
return result;
}
// 比较字符串方法一:将字符串转为数组
function filterString(str1, str2) {
var result = '';
var arr1 = str1.trim().split(''),
arr2 = str2.trim().split('');
arr1.some(function (item, index) {
if( item === arr2[index] ){
result += item;
return false;
}
return true;
});
return result;
}
// 比较字符串方法二:通过字符串下标比较
function filterString(str1, str2) {
var result = '';
for( var i = 0; i < str1.length; i++ ){
if( str1[i] === str2[i] ){
result += str1[i];
continue;
}
return result;
}
return result; // 当两个比较的字符串一模一样的时候就会走到这里
}死办法,循环比较 终止
let array = ["flower","flow","flght", ...]
function parse(arr){
let repetition = array[0]
arr.forEach(a=>{
for(let i=repetition.length-1;i>=0;i--){
repetition = repetition.split("",i+1).join("")
if(a.indexOf(repetition) > -1) return
if(i === 0) repetition = ""
}
})
return repetition;
}
console.log(parse(array))公共指针法
function maxPrefix(strs) {
if (!strs || !strs.length) {
return '';
}
// 从0开始依次比较
let currentIndex = 0;
while (true) {
// 取第一个字符串的当前位字符作为参照
const refer = strs[0][currentIndex];
// 是否全部匹配
const currentAllMatch = strs.reduce((pre, str) => {
return pre && str.charAt(currentIndex) === refer;
}, true);
if (currentAllMatch) {
currentIndex ++;
} else {
break;
}
}
return strs[0].substring(0, currentIndex);
}解法一:逐个比较
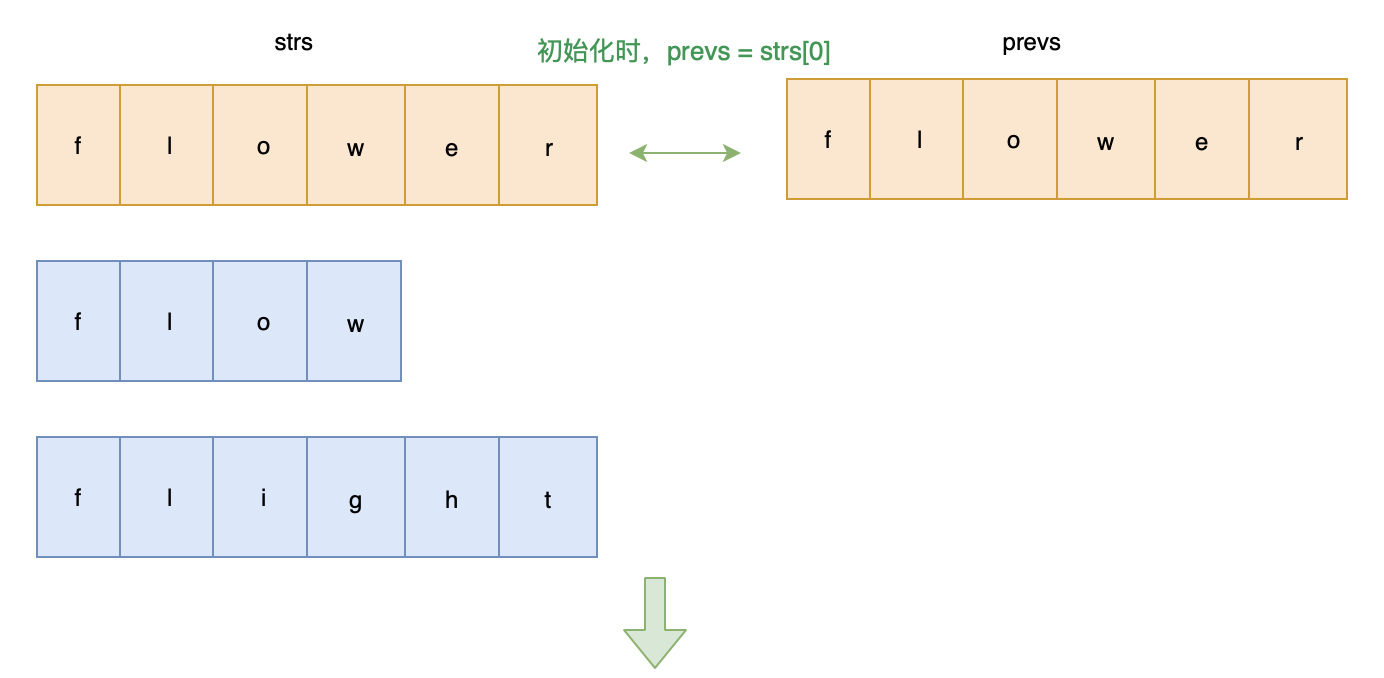
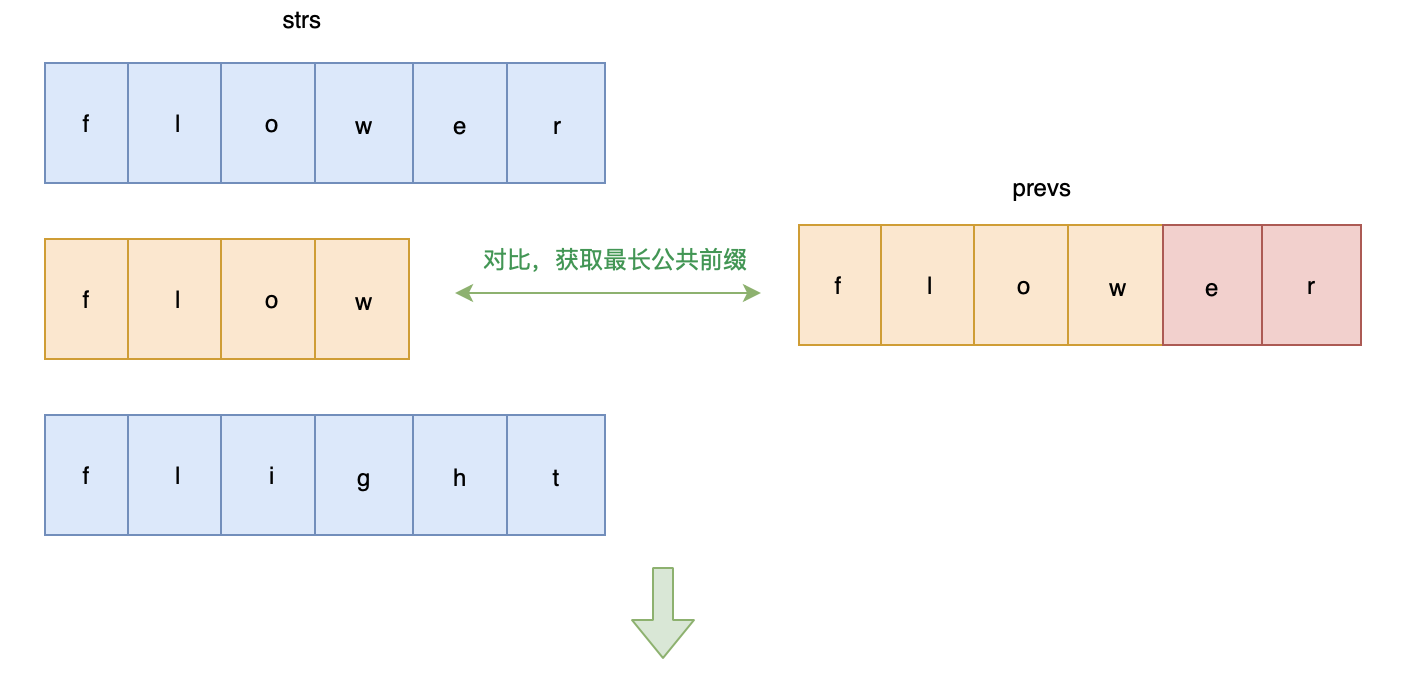
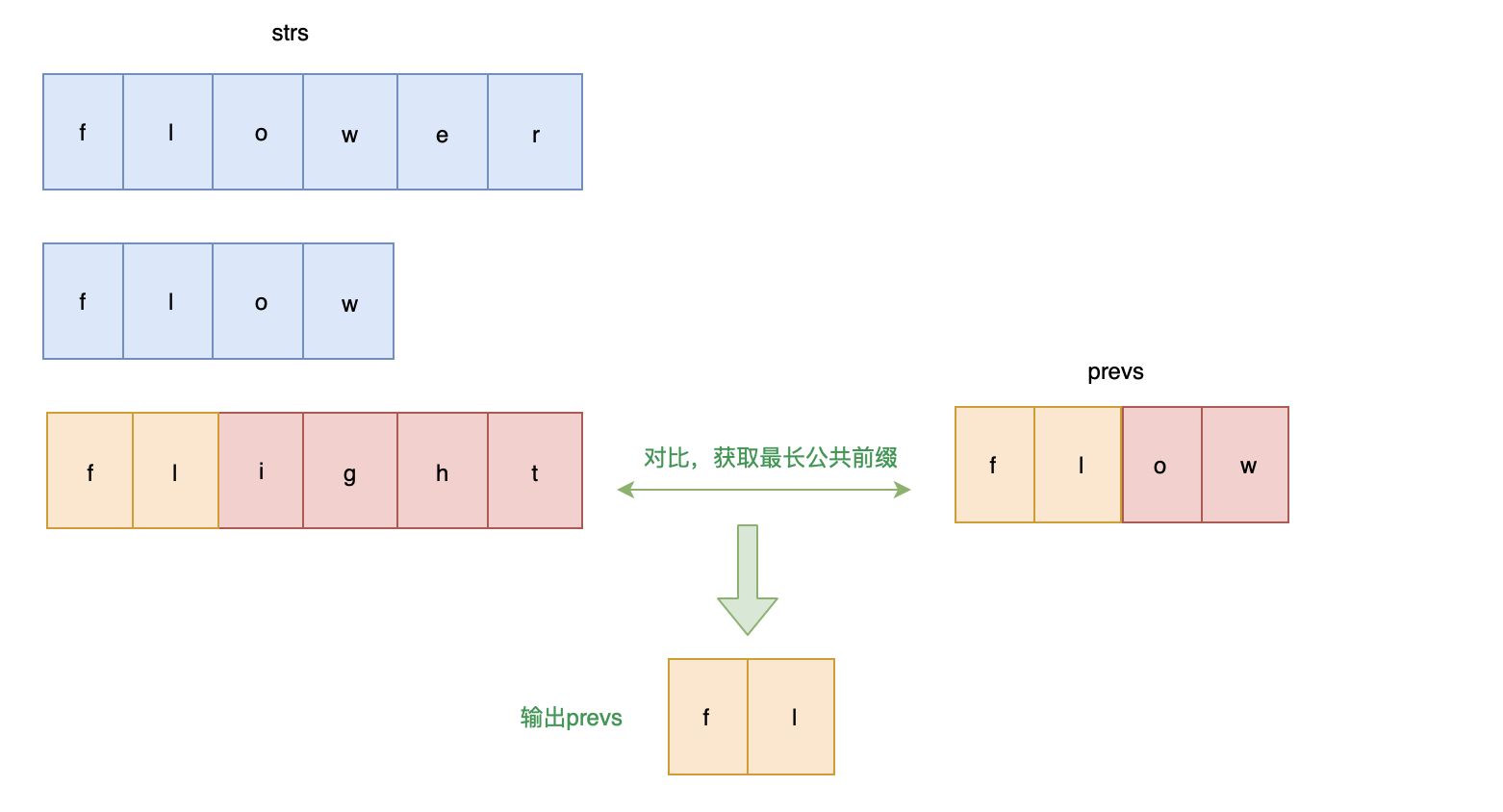
解题思路: 从前往后依次比较字符串,获取公共前缀
画图帮助理解一下:
代码实现:
var longestCommonPrefix = function(strs) {
if (strs === null || strs.length === 0) return "";
let prevs = strs[0]
for(let i = 1; i < strs.length; i++) {
let j = 0
for(; j < prevs.length && j < strs[i].length; j++) {
if(prevs.charAt(j) !== strs[i].charAt(j)) break
}
prevs = prevs.substring(0, j)
if(prevs === "") return ""
}
return prevs
};时间复杂度:O(s),s 是所有字符串中字符数量的总和
空间复杂度:O(1)
解法二:仅需最大、最小字符串的最长公共前缀
解题思路: 获取数组中的最大值及最小值字符串,最小字符串与最大字符串的最长公共前缀也为其他字符串的公共前缀,即为字符串数组的最长公共前缀
例如 abc 、 abcd 、ab 、ac ,最小 ab 与最大 ac 的最长公共前缀一定也是 abc 、 abcd 的公共前缀
画图帮助理解一下:
代码实现:
var longestCommonPrefix = function(strs) {
if (strs === null || strs.length === 0) return "";
if(strs.length === 1) return strs[0]
let min = 0, max = 0
for(let i = 1; i < strs.length; i++) {
if(strs[min] > strs[i]) min = i
if(strs[max] < strs[i]) max = i
}
for(let j = 0; j < strs[min].length; j++) {
if(strs[min].charAt(j) !== strs[max].charAt(j)) {
return strs[min].substring(0, j)
}
}
return strs[min]
};时间复杂度:O(n+m),n是数组的长度, m 是字符串数组中最短字符的长度
空间复杂度:O(1)
解法三:分治策略 归并**
分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。
这道题就是一个典型的分治策略问题:
- 问题:求多个字符串的最长公共前缀
- 分解成多个相似的子问题:求两个字符串的最长公共前缀
- 子问题可以简单求解:两个字符串的最长公共前缀求解很简单
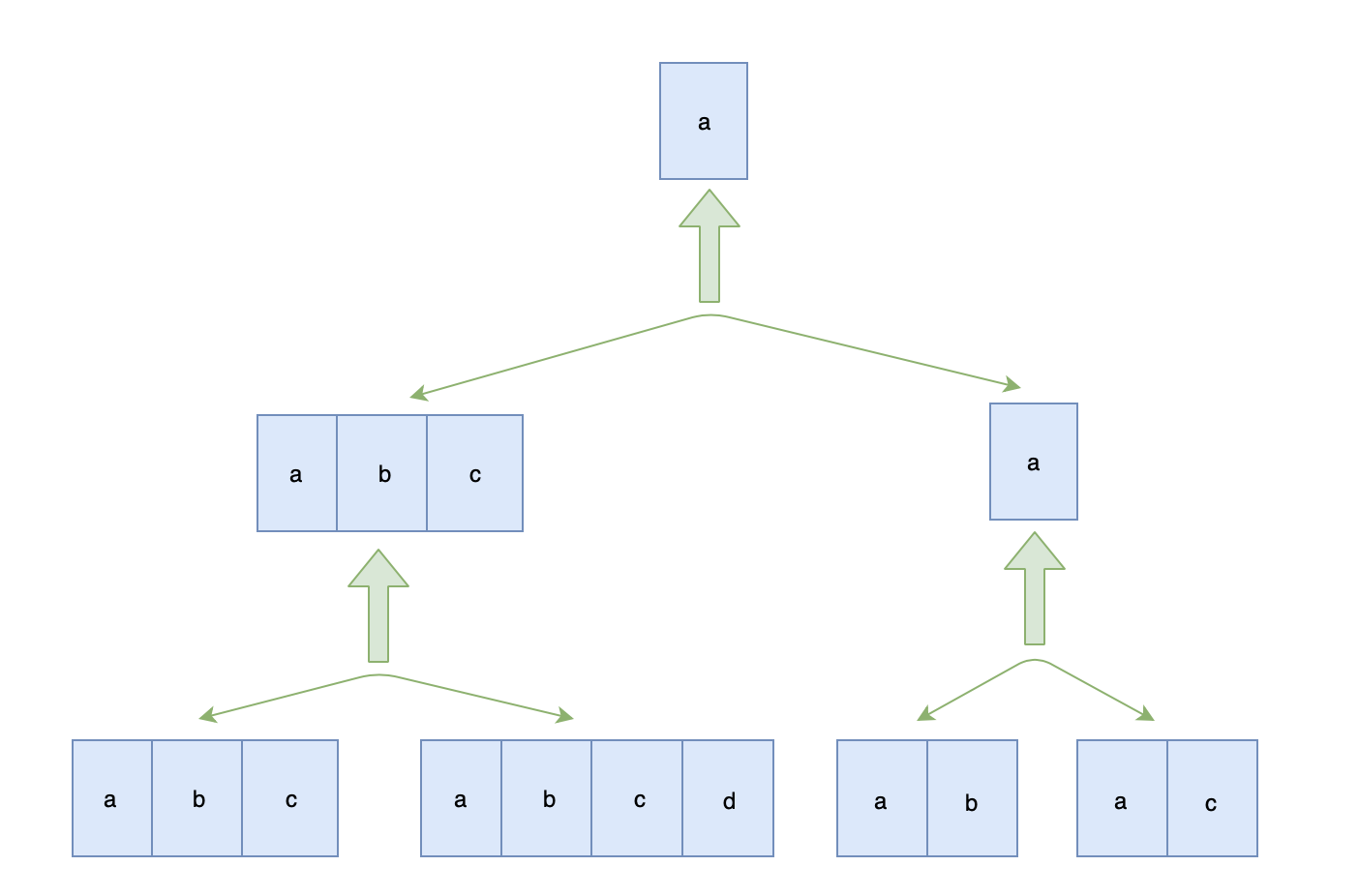
- 原问题的解为子问题解的合并:多个字符串的最长公共前缀为两两字符串的最长公共前缀的最长公共前缀,我们可以归并比较两最长公共前缀字符串的最长公共前缀,知道最后归并比较成一个,则为字符串数组的最长公共前缀:
LCP(S1, S2, ..., Sn) = LCP(LCP(S1, Sk), LCP(Sk+1, Sn))
画图帮助理解一下:
以 abc 、 abcd 、ab 、ac 为例:
代码实现:
var longestCommonPrefix = function(strs) {
if (strs === null || strs.length === 0) return "";
return lCPrefixRec(strs)
};
// 若分裂后的两个数组长度不为 1,则继续分裂
// 直到分裂后的数组长度都为 1,
// 然后比较获取最长公共前缀
function lCPrefixRec(arr) {
let length = arr.length
if(length === 1) {
return arr[0]
}
let mid = Math.floor(length / 2),
left = arr.slice(0, mid),
right = arr.slice(mid, length)
return lCPrefixTwo(lCPrefixRec(left), lCPrefixRec(right))
}
// 求 str1 与 str2 的最长公共前缀
function lCPrefixTwo(str1, str2) {
let j = 0
for(; j < str1.length && j < str2.length; j++) {
if(str1.charAt(j) !== str2.charAt(j)) {
break
}
}
return str1.substring(0, j)
}时间复杂度:O(s),s 是所有字符串中字符数量的总和
空间复杂度:O(m*logn),n是数组的长度,m为字符串数组中最长字符的长度
解法四:Trie 树(字典树)
Trie 树,也称为字典树或前缀树,顾名思义,它是用来处理字符串匹配问题的数据结构,以及用来解决集合中查找固定前缀字符串的数据结构。
解题思路: 构建一个 Trie 树,字符串数组的最长公共序列就为从根节点开始遍历树,直到:
-
遍历节点存在超过一个子节点的节点
-
或遍历节点为一个字符串的结束字符
为止,走过的字符为字符串数组的最长公共前缀
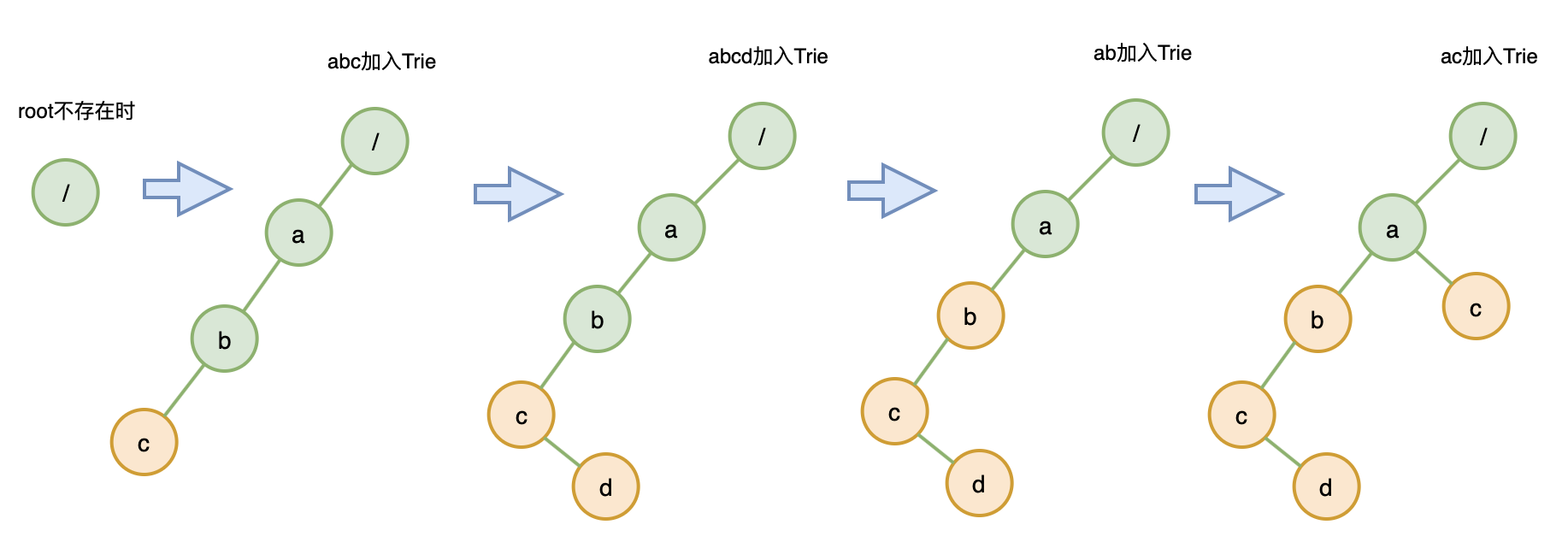
画图帮助理解一下:
构建一个 Trie 树,以 abc 、 abcd 、ab 、ac 为例:
代码实现:
var longestCommonPrefix = function(strs) {
if (strs === null || strs.length === 0) return "";
// 初始化 Trie 树
let trie = new Trie()
// 构建 Trie 树
for(let i = 0; i < strs.length; i++) {
if(!trie.insert(strs[i])) return ""
}
// 返回最长公共前缀
return trie.searchLongestPrefix()
};
// Trie 树
var Trie = function() {
this.root = new TrieNode()
};
var TrieNode = function() {
// next 放入当前节点的子节点
this.next = {};
// 当前是否是结束节点
this.isEnd = false;
};
Trie.prototype.insert = function(word) {
if (!word) return false
let node = this.root
for (let i = 0; i < word.length; i++) {
if (!node.next[word[i]]) {
node.next[word[i]] = new TrieNode()
}
node = node.next[word[i]]
}
node.isEnd = true
return true
};
Trie.prototype.searchLongestPrefix = function() {
let node = this.root
let prevs = ''
while(node.next) {
let keys = Object.keys(node.next)
if(keys.length !== 1) break
if(node.next[keys[0]].isEnd) {
prevs += keys[0]
break
}
prevs += keys[0]
node = node.next[keys[0]]
}
return prevs
}时间复杂度:O(s+m),s 是所有字符串中字符数量的总和,m为字符串数组中最长字符的长度,构建 Trie 树需要 O(s) ,最长公共前缀查询操作的复杂度为 O(m)
空间复杂度:O(s),用于构建 Trie 树
leetcode
死办法,循环比较 终止
let array = ["flower","flow","flght", ...] function parse(arr){ let repetition = array[0] arr.forEach(a=>{ for(let i=repetition.length-1;i>=0;i--){ repetition = repetition.split("",i+1).join("") if(a.indexOf(repetition) > -1) return if(i === 0) repetition = "" } }) return repetition; } console.log(parse(array))
charAt 可以用起来
0 前言
对于解法二的原理我思考了好一会儿才明白, 原理挺巧妙的,还利用到了 js 比较操作符简化了排序的工作. 写下这些文字是因为对于解法二的时间复杂度分析, 我和 @sisterAn 有不同的结果.
sisterAn:O(n+m),n是数组的长度, m 是字符串数组中最短字符的长度
我: O(S),S 是所有字符串中字符数量的总和。
另外这里还基于时间复杂度对解法二和解法一进行了对比.
1 字符串对比的时间复杂度分析
对于解法二的时间复杂度分析结果之所以不同, 就是对于strs[min] > strs[i]这一操作的时间复杂度计算不同, 即在 js 中字符串对比的时间复杂度到底是O(1)还是O(n)呢?
经查验应该是O(n), 而非 O(1)的.
因为比较字符串大小时用到了内置的比较操作符, 所以计算时间复杂度时应该考虑到比较操作的工作原理, 我特意去看了下MDN文档. 在Comparison operators中提到了字符串对比时的依据:
Strings are compared based on standard lexicographical ordering, using Unicode values.
我的理解是按照字符串的书写顺序(中英文都是自左到右, 阿拉伯文自右到左), 依次比较它们的 Unicode 值. 然后我在 Array 的 sort() 方法中也找到了类似的佐证
The default sort order is ascending, built upon converting the elements into strings, then comparing their sequences of UTF-16 code units values.
数组对比时会先把元素转为字符串, 然后按照它们的 UTF-16 码元的次序依次对比码元的值.
举例: "abcd < abdd"
- 先比较
"a""a", 二者相同, 继续对比下一个字符; - 再比较
"b""b", 二者相同, 继续对比下一个字符. "c"的 Unicode 值比"d"的 Unicode 值要小, 不再对比下一位字符, 直接得到比较结果:true
注意这里的比较过程和解法一中比较两个字符串的公共前缀的过程很像: 当同一索引处两个字符不同时就退出比较, 这一点在后面对比解法一和解法二时会用到.
关于算法时间复杂度的探索心路历程见末尾的补充.
2 解法二时间复杂度分析
2.1 分析过程
借鉴 leetcode-cn 官方题解中给出的算法复杂度分析, 考虑最坏情况, n 个字符串都相同, 字符串长度为 m. 不想看过程可以直接看 2.2 分析结果
解法二代码如下:
var longestCommonPrefix = function(strs) {
if (strs === null || strs.length === 0) return "";
if(strs.length === 1) return strs[0]
let min = 0, max = 0
for(let i = 1; i < strs.length; i++) {
if(strs[min] > strs[i]) min = i
if(strs[max] < strs[i]) max = i
}
for(let j = 0; j < strs[min].length; j++) { // m 次循环
if(strs[min].charAt(j) !== strs[max].charAt(j)) {
return strs[min].substring(0, j)
}
}
return strs[min]
};代码的核心分两部分, 第一部分是求最大和最小字符串:
for(let i = 1; i < strs.length; i++) { // n 次循环
if(strs[min] > strs[i]) min = i // 最坏情况下进行了 m 次对比, 每次对比是 O(1) 的时间开销
if(strs[max] < strs[i]) max = i // 最坏情况下进行了 m 次对比
}分析可知, 该部分代码进行 n 次循环, 每次循环都进行了 2m 次单字符的比较操作, 时间复杂度为: O(n * 2m)
代码的第二部分: 对比最大和最小字符串
for(let j = 0; j < strs[min].length; j++) { // m 次循环
if(strs[min].charAt(j) !== strs[max].charAt(j)) { // O(1) 的时间开销
return strs[min].substring(0, j)
}
}分析可知, 该部分代码对比最大和最小字符串时进行了 m 次单字符的比较操作, 时间复杂度为: O(m)
2.2 分析结果
合并两部分代码的时间复杂度, 得到最差情况下解法二的时间复杂度为: O(S)
推导: O(n * 2m) + O(m) = 2 * O(n * m) + O(m), 略去常数系数 2 和低阶项O(m), 即 O(S).
3 对比解法一和解法二: 基于时间复杂度
3.1 结论
解法二看起来比较优雅, 但是相对解法一有重复的操作, 时间复杂度更高.
3.2 证明
首先举一个极端情况的例子来佐证结论, 如果有耐心的话再看后面对一般情况的分析.
3.2.1 极端情况
cosnt strs = ['ab', 'abcd', 'z', 'abcdef']
对于解法一, 对比到第 3 个字符'z'时就可以得到最长公共前缀的结果是'';
解法二需要全部比较完后, 再对比 'ab' 和 'z'才能得到结论.
3.2.2 一般情况
首先, 解法一和解法二都对字符串数组进行 n 次循环, 每次循环中会涉及两个字符串的对比.
在上面我们提到了, 解法二中两个字符串的大小比较算法和解法一中求两个字符串的公共前缀的过程是类似的, 其时间复杂度也一样.
但是解法二在每次循环时, 为得到最大和最小字符串, 要进行两组字符串的对比, 所以花费时间是两倍.
其次, 解法二中在循环过程后还需要再对比最大和最小字符串才能得到最长公共前缀. 但是其实最大和最小字符串在之前的循环过程中已经比较过了, 不仅增加的时间复杂度, 更重要的是对于公共前缀为空的情况无法提前退出循环.
4 补充
在查找字符串大小对比的算法时间复杂度时, 一路追踪到了规范, 最后还写了一个测试来佐证自己的猜测, 这里主要记录在面对查找字符串大小对比的算法时间复杂度这一问题时的探索路径.
4.1 规范
先去查找规范中 comparison operator的章节:
The comparison x < y, where x and y are values,
....
If Type(x) is String and Type(y) is String, then
If IsStringPrefix(y, x) is true, return false.
If IsStringPrefix(x, y) is true, return true.
Let k be the smallest nonnegative integer such that the code unit at index k within x is different from the code unit at index k within y. (There must be such a k, for neither String is a prefix of the other.)
Let m be the integer that is the numeric value of the code unit at index k within x.
Let n be the integer that is the numeric value of the code unit at index k within y.
If m < n, return true. Otherwise, return false.
自己的理解是:
对于 x < y ,如果 x 和 y 都是字符串时:
- 如果 y 是 x 的前缀, 则返回 false;
- 如果 x 是 y 的前缀, 则返回 true;
- x 和 y 互不为前缀时, 从索引 0 开始肯定有索引 k, 使得 x 和 y 对应索引处的码元的数值大小不同, 对比索引 k 处二者码元的数值大小.
从以上步骤可以看出, 最差情况下字符串大小比较算法最多会走以上 3 步流程, 现推导其最差情况的时间复杂度, 举例如下:
const str1 = 'abcd'
const str2 = 'abcf'两字符串长度相同, 互不为前缀, 但仅最后 1 个字符不同. 直到第 3 步遍历至最后 1 个字符时才能得到大小判断结果, 符合最差情况.
此时第 1 步和第 2 步中用到了 IsStringPrefix(x, y)方法, 时间复杂度未知;
第 3 步同步遍历两个字符串到末尾, 时间复杂度为线性, O(m), m 为字符串长度.
为推导字符串大小比较算法的时间复杂度, 需要知道 IsStringPrefix(x, y)方法的时间复杂度, 查阅规范中IsStringPrefix(x, y)的规定:
IsStringPrefix ( p, q )
The abstract operation IsStringPrefix takes arguments p (a String) and q (a String). It determines if p is a prefix of q. It performs the following steps when called:
Assert: Type(p) is String.
Assert: Type(q) is String.
If q can be the string-concatenation of p and some other String r, return true. Otherwise, return false.
规范中只是说如果 q可由p和其他字符拼接而成, 就说明p是q的前缀, 返回true, 并未给出如何判断是否可拼接的细节. (找到这里真是太难了....)
下面怎么办, 只能一本正经的猜猜猜了...
4.2 猜测与验证
猜测引擎对IsStringPrefix(x, y)的实现关键仍然是依次对比相同索引处码元, 也就是IsStringPrefix(x, y)算法的时间复杂度是 O(m), m为公共前缀的长度.
下面进行验证, 因为测试代码只能是x < y, 需要借助字符串大小比较来间接测试IsStringPrefix()方法的时间复杂度. 为保证测试结果尽可能只含有IsStringPrefix()的耗时, 所选测试用例都仅走第 1 步IsStringPrefix(y, x)就返回结果, 即 y 是 x 的前缀.
经实例测试, Chrome V80.0.3987 的 V8 引擎中的测试结果如图:

结果表明, 当保持 x 的长度不变, 线性扩大 y 的长度时, IsStringPrefix(y,x)的耗时也呈线性规模增长.
即最差情况下IsStringPrefix(y,x)的时间复杂度是O(m), m 为公共前缀长度.
4.3 结论
承接 4.1 节中关于最差情况下字符串大小比较算法的时间复杂度的推导:
第 1 步: IsStringPrefix(y, x), 时间复杂度 O(n), n 为字符串长度;
第 2 步: IsStringPrefix(x, y), 时间复杂度 O(n);
第 3 步: 同步遍历两个字符串到末尾, 时间复杂度 O(n)
综上, 最差情况下字符串大小对比算法的时间复杂度是: O(n), 非 O(1).
参考:
/**
* 最长公共前缀
* @param {*} arr
* 方法1思路:
* 1、最短项的长度
* 2、按长度获取可能的公共前缀,没有公共项或者达到“1、”的长度后结束遍历
* 3、返回所有公共集合中的最长项
*/
function getMaxCommonPrefix1(arr) {
if (!arr || !Array.isArray(arr) || !arr.length) return '';
if (arr.length === 1) return arr[0];
const minItemLength = getItem(arr, false).length;
const startsWidth = (str, start) => str.indexOf(start) === 0;
// MAX:true获取最长的项,false获取最短的项
function getItem(list, MAX = true) {
return list.reduce((prev, cur) => {
if (cur.length > prev.length === MAX) prev = cur;
return prev;
}, list[0]);
}
// 按长度获取所有公共前缀的集合
function getCommon(list, len = 1, allCommon = []) {
const commonStr = list[0].substr(0, len);
const invalid = list.some((i) => !startsWidth(i, commonStr));
if (invalid || len > minItemLength) return allCommon;
return getCommon(list, len + 1, [...allCommon, commonStr]);
}
// 返回所有公共前缀中最长的项
return getItem(getCommon(arr)) || '';
}
// 方法2:利用charAt对比
function getMaxCommonPrefix2(arr) {
if (!arr || !Array.isArray(arr) || !arr.length) return '';
if (arr.length === 1) return arr[0];
let maxCommonPrefix = '';
const minItem = getMinItem(arr);
const minItemArr = minItem.split('');
const leftArr = arr.filter((i) => i !== minItem);
function getMinItem(list) {
return list.reduce((prev, cur) => {
if (cur.length < prev.length) prev = cur;
return prev;
}, list[0]);
}
for (let i = 0; i < minItemArr.length; i++) {
// 只要有一个不是所有item都有的,就退出循环
if (leftArr.some((item) => minItemArr[i] !== item.charAt(i))) break;
maxCommonPrefix += minItemArr[i];
}
return maxCommonPrefix;
}
// const g = getMaxCommonPrefix1;
const g = getMaxCommonPrefix2;
console.log(g(['acs', 'a1c', 'acsk', 'acsk'])); // a
console.log(g(['acs', 'fac', 'acsk', 'acsk'])); // ''
console.log(g(['acs'])); // 'acs'
console.log(g([])); // ''var arr = ["flower","flow","flight"];
var flag = true, len = 0;
while(flag) {
if (arr.every(v => len < v.length && v[len] === arr[0][len])) {
len++;
} else {
flag = false;
}
}
console.log(len);
不会算法,用正则强行撸一波。
var result
var reg = /^(\w+)([^,]*),(\1[^,]*,)*\1([^,]*)$/
var arr = ['filower', 'filow', 'filight', 'filat', 'filoat', 'filf']
// var arr = ['flower', 'flow', 'flight']
var m = arr.join(',').match(reg)
result = m ? m[1] : ''
console.log(result)/**
* @param {string[]} strs
* @return {string}
*/
var longestCommonPrefix = function(strs) {
if(!strs.length)return ''
if(strs.length==1)return strs[0]
let minItem = strs.find(i=>i.length===Math.min(...strs.map(i=>i.length)))
let ret = ''
for(let i=0;i<minItem.length;i++){
if(strs.every(item=>item.slice(0,i+1) === minItem.slice(0,i+1)) ){
ret = minItem.slice(0,i+1)
}
}
return ret
};用数组中的第一个字符串作为基准
匹配后面每个字符串是否都有公共部分,有就退出循环,没有就继续查找
const overlap = function(arr) {
const [first] = arr
if(arr.length <= 1) return first
let result = first
for(let i = 0; i < first.length; i ++) {
const isOverlap = arr.every(item => item.indexOf(result) !== -1)
if(isOverlap) {
break
}
result = result.substr(0, first.length - i)
}
return result
}
const getString = arr => {
const minLen = Math.min(...arr.map(item=>(item.length)));
let str = "";
for(let i=0;i<minLen;i++){
const strItem = arr[0][i];
if(arr.every((item,index)=>(item[i] === strItem))){
str = `${str}${strItem}`
}
}
return str
}
['flat', 'flany', 'flabc'].reduce((curr, next, index, arr) => {
if(index && !curr) return ""
if(arr.every(item => item[index] === arr[0][index])){
return `${curr}${tar}`
}
return curr
}, '')
const strArr = ['asdfg', 'awer', 'aswq']
function twoCommonPrefix(str1, str2) {
let p = 0
let n = 0
let common = ''
while (true) {
if (str1[p] === str2[n] && p < str1.length && n < str2.length) {
common += str1[p]
p++
n++
} else {
return common
}
}
}
function commonPrefix(strArr) {
if (!Array.isArray(strArr) || strArr.length === 0) return ''
return strArr.reduce(twoCommonPrefix)
}
function commonPrefix1(strArr) {
let min = 0
let max = 0
for (let i = 0; i < strArr.length; i++) {
if (strArr[min] > strArr[i]) min = i
if (strArr[max] < strArr[i]) max = i
}
return twoCommonPrefix(strArr[min], strArr[max])
}
console.log(commonPrefix1(strArr))
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) return "";
String result = strs[0];
for (int i = 1; i < strs.length; i++) {
String temp = getCommonPrefix(result, strs[i]);
if(temp.equals("")) return "";
result = temp;
}
return result;
}
public String getCommonPrefix(String first, String second){
StringBuilder s = new StringBuilder();
int length = Math.min(first.length(), second.length());
for (int i = 0; i < length; i++) {
if (first.charAt(i) == second.charAt(i)) {
s.append(first.charAt(i));
} else {
break;
}
}
return s.toString();
}
}const longestCommonPrefix = (strs) => {
if (!strs.length) {
return ''
}
const compareTwo = (str1, str2) => {
let i = 0
while (i < str1.length && i < str2.length) {
if (str1[ i ] !== str2[ i ]) {
break
}
i++
}
return str1.slice(0, i)
}
return strs.reduce((result, it) => {
return compareTwo(result, it)
})
}
var longestCommonPrefix = function (strs) { strs = strs.sort((a, b) => a - b); for (let j = 0; j < strs[0].length; j++) { if (strs[0].charAt(j) !== strs[strs.length - 1].charAt(j)) { return strs[0].substring(0, j); } } return strs[0]; };
const overlap = (arr) => {
let str = arr[0]
let count = 0
//使用递归
let fun = (i, s) => {
if (i > arr.length - 1) {
return
}
let c = arr[i] //比较的值
let b = '' //相同的值
for (let i = 0; i < c.length; i++) {
if (c[i] === s[i]) {
b += c[i]
}
}
str = b
count++
fun(count, str)
}
fun(count, str)
return str
}
- 先以数组长度排序,短的放前面。
- 用map来去重,没有重复的时候就是各个字段串的前缀
var longestCommonPrefix = function (strs) {
if (strs.length == 1) return strs[0];
let prefix = "";
let map = new Map();
// 排序
strs = strs.sort((a, b) => a.length - b.length);
let pointer = strs[0].length;
while (pointer >= 0) {
for (let i = 0; i < strs.length; i++) {
let slice = strs[i].slice(0, pointer);
map.set(slice, slice);
}
// 如果map的长度超过1,就是有不一样的
if (map.size > 1) {
pointer--;
map.clear();
} else {
break;
}
}
prefix = strs[0].slice(0, pointer);
return prefix;
};function getMostCommonPart(nums){
let first = nums.shift()
let k = 0
let count = 0
let flag = true
while(k<first.length&&flag){
let c = first.charAt(k)
flag = nums.every(it=>it.charAt(k)===c)
flag&&count++
k++
}
return first.slice(0,count)
}
console.log(getMostCommonPart(["dog","racecar","car"]))
console.log(getMostCommonPart(["flower","flow","flight"]))