- A constrained brute force algorithm on hardware is used to solve a sudoku.
- When a valid fill is not found backtracking is done.
- Backtracking is repeated until the last number is the valid guess, i.e. guess out of 1 to 9.
- Digital logic realised using priority encoders and multiplexers.
Sudoku contains 81 cells, in a 9×9 grid. Each row, column and block can include a serial number from 1 to 9.
Proper Sudokus have one solution. A brute force algorithm can be used to solve sudoku on computers. This algorithm visits an empty cell and fills it sequentially till a valid fill is not possible. When valid fill is not found then backtracking is done to change a previously allotted sequential bit to other numbers. After writing this new number, the solver again attempts to fill all empty cell until further violations occur or all cells get filled. This is repeated until the allowed value in the last (81st) cell is a valid guess.
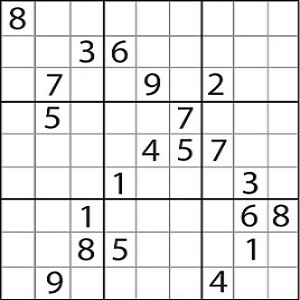
Hardest Sudoku: A typical example to run comparative study,
A simple C code is written to solve sudoku using basic Backtracking problems. A recursive function is defined which stacks up until an end condition is met. Thus, assigning numbers to next empty cell found in the puzzle before checking if its a valid entry or not. A simple check that same entry is not present in its corresponding row, column and block. After reviewing the number is assigned and again calling the same assignment function recursively to satisfy the end test that this assignment would lead to a solution of puzzle or not. If not, try the next number before checking for its validity.
Hence, only the row and column of the unassigned cell are checked for conflict from digits one to nine. If there is no conflict at row column and block, that is, recursion is successful, return true but if not, remove the digit assigned and try another. If all numbers fail, return false. Thus, this will cause the previous function called in recursion to change the digit it selected then. Until all the recursions return true, a puzzle is still getting solved. When no empty cell is left, the puzzle is solved.
This method serves many advantages. Firstly, it guarantees a solution; however, a user should enter a valid puzzle. It is a simple algorithm but, it takes a long time and is proved to be slow compared to other advanced algorithms. Such an algorithm may typically require as few as 15,000 cycles, or as many as 900,000 cycles to solve a Sudoku. Solving sudoku can also be modelled as a constraint satisfaction problem.
Reasoning based constraints can be applied to solve as well as model a problem. So, incorporating an algorithm, where backtracking and constraint-based reasoning would be able to reduce the time to compute and solve all type of sudoku. Following is the above-mentioned sudoku game, where zero represents an empty cell.
Bitmaps are used to constraint the validity of an element for a certain cell. Thus, bitmaps represent a constraint that such elements are already present in a row or column or block. The puzzle is searched for an empty cell.
When a cell is found, a valid element is evaluated based on the candidate selection table defined in the FSM later. Thus, a brute force method could be efficient when combined with an elimination method.
When the puzzle is loaded, i.e. start=1, the algorithm starts. FSM will goto next empty state where the next empty element is determined. It is a simple logic of priority encoder where the first zero found element's index is reported as a selected row, selected column and selected block. Now, machine proceeds to guess state.
The above-mentioned bitmaps are used to generate the candidate selection table. Every bitmap contains the information that whether a particular cell is occupied (1) or empty (0). This information about elements that are yet to be occupied in a parttcular row, column and block is fed to a priority encoder.
Randomly selecting a number would make it difficult to backtrack as then we have to keep track of it. Also, the first number which will always be the least valid number which can be filled onto that cell can be used. It would help in creating logic for backtracking as will be explained further as FSM proceeds.
In the above example, the first empty cell was (1,2) thus making candidate selection table for the first row, second column and first block.
This represents that 1,2,4 and 6 are valid elements which can be filled. As mentioned earlier, selecting "1" as a valid element FSM proceeds further. When this cell is filled, its bitmaps are also updated correspondingly. Also, this element and its address location is filled onto the stack to remember which element was filled where. This process of finding empty cells and filling repeats until sudoku completes or some violation occurs. When a violation occurs, it means that the candidate selection table cannot find any zero entry in it. Thus, we need to backtrack and check for the last filled cell. It is backtracked by poping a value from the stack where its address was stored.
This particular address is read, and its element is stored. Its location is cleared, and again bitwise ORing test of bitmaps is done to find the valid elements which can be filled. Now a valid symbol other than the one which was already put in it is selected. Thus, sequentially next larger element than the one restored from the stack is selected from the valid list and further filling of puzzle proceeds. Eventually, the algorithm fills in the last empty cell.
Example Sudoku Under Test:
Thus, 19.811 micro-seconds took for VHDL code to solve sudoku. The clock period was 100 picosecond.For 2.3GHz, 138,690,000 clock cycles are used up by code—however, 198,114 clock cycles used by VHDL.
If the clock were 2.3GHz for VHDL, then the time taken would be, 86 micro-sec which is less than 60.3 milli-sec as in C code backtracking.
Goto Report for all details.....