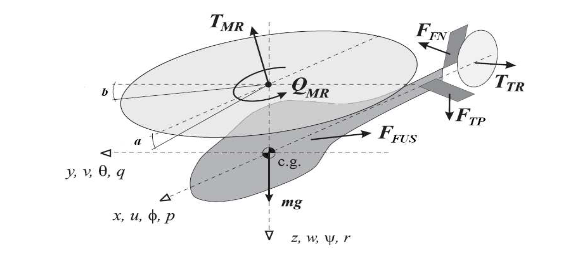
The aim of the paper is the application of three different design techniques for the hovering control of a Yamaha R-MAX helicopter. The Yamaha R-MAX is a gasoline-powered UAV, controlled in line of sight by the user via a remote controller. It was designed primarily to be used in agriculture.
The mathematical model of a helicopter is clearly non-linear and the equations to be used change according to the flight regime. In this paper we will focus on low-speed flight, whose model can be linearized and, with the appropriate simplifications, reduced to a system of order 13.
The control quantities are:
-
Lateral Cyclic: allows you to tilt the main rotor so as to move the thrust vector sideways allowing the helicopter to move in that direction.
-
Longitudinal Cyclic: like the lateral cyclic, it allows you to move longitudinally.
-
Rudder: allows you to control the direction in which the nose of the helicopter is pointing. The rudder works by changing the angle of incidence of the tail rotor, increasing or decreasing its thrust in the desired direction.
-
Collective pitch: allows you to vary the angle of incidence of the main rotor blades at the same time. By increasing the collective pitch, the vertical thrust is increased and the helicopter rises, while decreasing it reduces the thrust and the helicopter descends.
The control input vary between -1 and 1 (dimensionless). The validity regime of the model is such that if the control works well, the control quantities should always remain far from the limit values. In the Simulink simulation schemes, however, saturation blocks that simulate the physical limit of the actuators have been inserted.
The settling time should be about 5 seconds. Overshooting should be low (maximum 15-20%). In this context, a lower overshooting is preferable even if this leads to a slight increase in settling time.
The outputs of the model are the three translational speeds u, v and w, and the rotation speed about the vertical axis yaw rate measured by the gyroscopic yaw rate sensor.
An extensive discussion of the presented work can be found here (in English) or here (in Italian).
Since the paper was intended for an Italian exam, it was originally written in Italian, and each part has now been translated using automated software.
L'obiettivo dell'elaborato è l'applicazione di tre diverse tecniche di progetto per il controllo di hovering di un elicottero Yamaha R-MAX. Lo Yamaha R-MAX è un UAV alimentato a benzina, comandato in linea di vista dall'utente tramite un telecomando. È stato progettato principalmente per essere utilizzato in ambito agricolo.
Il modello matematico di un elicottero è chiaramente non lineare e le equazioni da utilizzare cambiano in base al regime di volo. In questo elaborato ci si concentrerà sul volo a bassa velocità, il cui modello può essere linearizzato e, con le opportune semplificazioni, ridotto ad un sistema di ordine 13.
Le grandezze di controllo sono:
-
Lateral Cyclic: permette di inclinare il rotore principale in modo da spostare il vettore di spinta lateralmente consentendo all'elicottero di muoversi in tale direzione.
-
Longitudinal Cyclic: come il lateral cyclic, permette di muoversi longitudinalmente.
-
Rudder: permette di controllare la direzione verso cui punta il muso dell'elicottero. Il rudder funziona modificando l'angolo di incidenza del rotore di coda, aumentando o diminuendone la spinta nella direzione desiderata.
-
Collective pitch: consente di variare l'angolo di incidenza delle pale del rotore principale contemporaneamente. Aumentando il collective pitch, si aumenta la spinta verticale e l'elicottero sale, mentre diminuendolo si riduce la spinta e l'elicottero scende.
Le grandezze di controllo variano tra -1 ed 1 (adimensionali). Il regime di validità del modello è tale per cui se il controllo funziona bene, le grandezze di controllo dovrebbero rimanere sempre ben lontane dai valori limite. Negli schemi di simulazione Simulink, sono stati comunque inseriti i blocchi di saturazione che simulano il limite fisico degli attuatori.
Il tempo di assestamento deve essere di circa 5 secondi. La sovraelongazione deve essere bassa (massimo 15-20%). In questo contesto, una sovraelongazione più bassa è preferibile anche se ciò comporta un leggero aumento del tempo di assestamento.
Le uscite del modello sono le tre velocità traslazionali u,v e w, e la velocità di rotazione intorno all'asse verticale yaw rate misurata dal gyroscopic yaw rate sensor.
Questo progetto è stato sviluppato per l'esame Complementi di Controlli tenuto dal Prof. Pironti presso l'Università degli Studi di Napoli Federico II.