Large-scale dissipation vs. lateral entrainment question
Opened this issue · 2 comments
@vanroekel I have two questions about the large-scale dissipation rate (
- Why is
$\epsilon_{ls}$ diagnosed using a tendency equation (epstend) or through a simple $\epsilon_{ls}\propto KE^{3/2}/L$ closure, rather than by coupling it to the lateral entrainment/detrainment term (which Lappen and Randall say represents the transfer of energy from plume-scale to sub-plume scale turbulence)? - This
$\epsilon_{ls}$ term appears as a source in the sub-plume scale TKE budget, but why does it appear as a sink in the u2 and v2 budgets (multiplied by 2/3 in each budget)? Because of their large-scale and anisotropic dynamics, shouldn't most of the plume-scale energy be dissipated anisotropically through the lateral entrainment between plumes? I'm not sure how the energetic conservation between the plume-scale sinks and sub-plume scale sources of energy work when there is entrainment/detrainment of w2 and imposed dissipation of u2 and v2, but only the latter is fed into the sub-plume scale TKE sources?
The Lappen & Randall 2001 papers are not very clear about how they define the large-scale dissipation rate (
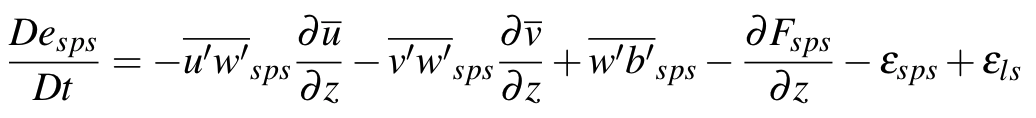
Despite not explicitly defining this dissipation rate, they discuss in the first paper that the entrainment/detrainment term represents the transfer of plume-scale TKE to sub-plume scale TKE. This suggests that
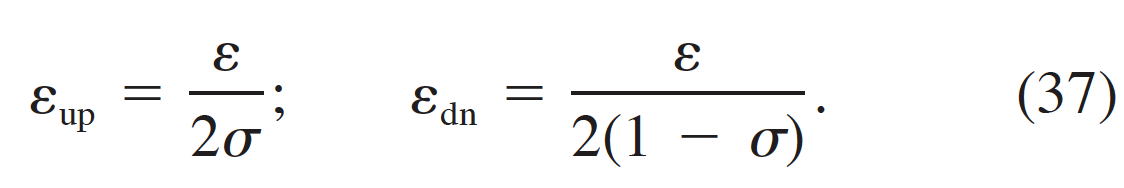
@amrapallig @qingli411 Do you have any thoughts on this? I noticed that Qing's version of the code has removed the dissipation tendency equation so that it is always estimated using the TKE/length scale closure.
So the u'2 and v'2 have been a tough one to think about for me. It is not clear those quantities are plume scale quantities to me. the MFC framework does not hold for momentum. Also at plume scale I would expect w'2 >> u'2 or v'2. I'm not sure we should cast dissipation as with the lateral entrainment detrainment terms. In my mind those should be a traditional HOC formulation. This is consistent with Lappen (1999) -- the dissertation where the 2001(a)-(c) papers stem from.
However, you could then question if the model is energetically consistent. Perhaps plume scale KE should be something like w'2 / 2 instead of the summation.
Regarding your second question, I think in Lappen and Randall (2001b) they argue the lateral entrainment/detrainment takes on the role of -2/3 epsilon. If that argument is to believed than think the model is consistent as is. So I'm not convinced eps_ls should be 1/6 or 1/2 of the entrainment/detrainment term
Finally the dissipation tendency equation was a thought on how to get rid of the Bogeault closure which is not feasible for global ocean simulations given how expensive the buoyancy calculation will be with a nonlinear EOS.
The TKE/length closure simply follows Cara-lynn's Dissertation. It is probably not the greatest idea given the source sink choices made in the model, unless we believe the lateral entrainment term takes on the role of -2/3 epsilon. If that is to be assumed though there seems no reason to use that formulation in the u2 and v2 budgets, even though those equations really aren't MFC applicable.
I guess I need to think about this more. Thanks for raising the issue.