🧮 Abacus

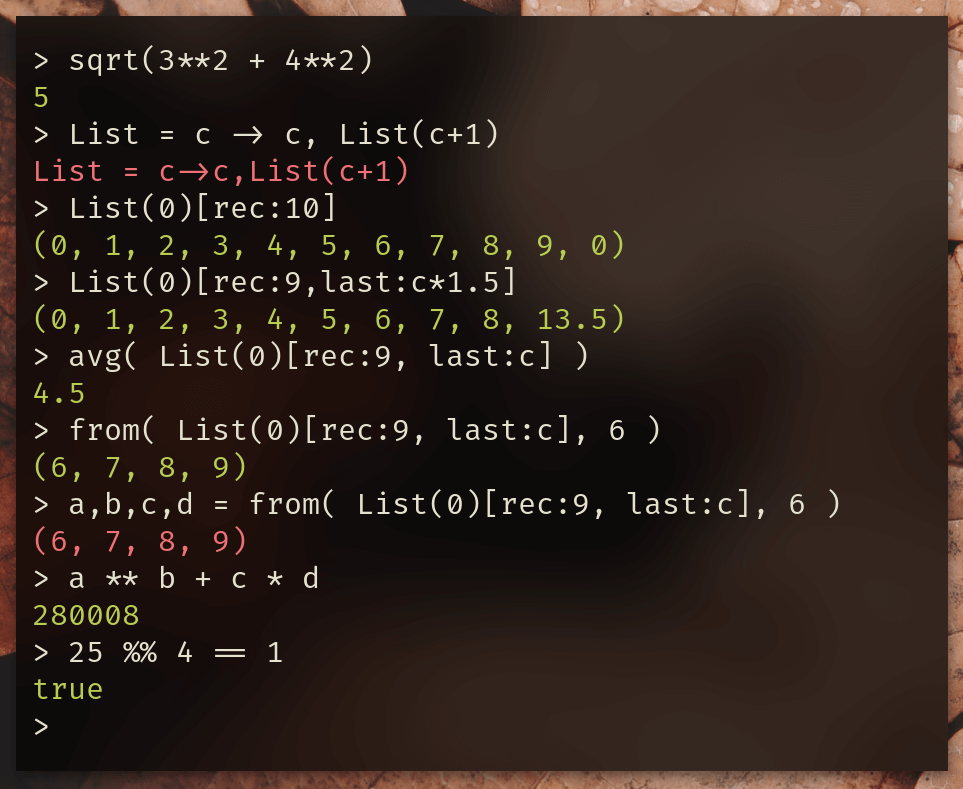
Abacus is a simple interactive calculator CLI with support for variables, lambdas, comparison checks, and math functions

λ abacus -h         

abacus - a simple interactive calculator CLI with support for variables, lambdas, comparison checks, and math functions

v1.4.0

Usage: abacus [--no-color] [--allow-copy] [--strict] [--precision PRECISION] [--eval EVAL] [--import IMPORT] [--prompt-symbol PROMPT-SYMBOL] [--answer-vars ANSWER-VARS]

Options:
  --no-color, -n         disable color in output [default: false]
  --allow-copy           Ctrl-C will copy current expression (if present) or last answer instead of aborting [default: false]
  --strict               prohibit use of undefined lambdas and variables [default: false]
  --precision PRECISION, -p PRECISION
                         precision for calculations [default: 64]
  --eval EVAL, -e EVAL   evaluate expression and exit
  --import IMPORT, -i IMPORT
                         import statements from file and continue
  --prompt-symbol PROMPT-SYMBOL
                         custom prompt symbol [default: > ]
  --answer-vars ANSWER-VARS
                         custom last answer variable names [default: ans,answer]
  --help, -h             display this help and exit
  --version              display version and exit

Install

Arch Linux

yay -S abacus-git

Manually

go install github.com/viktordanov/abacus@latest

Features

History of expressions and Tab completion of all math functions and defined variables

Importing from file (-i --import) lets you keep variable and lambda definitions in a file and import it on load

--import IMPORT, -i IMPORT
import statements from file and continue

> abacus -i definitions.a
> DefinedLambda(5) ...

Custom prompt symbol (--prompt-symbol) lets you use a custom string as a prompt prefix

 --prompt-symbol PROMPT-SYMBOL
 custom prompt symbol [default: > ]

$ abacus --prompt-symbol "🌱 "
🌱 2+2
4
🌱 ...

Evaluate and exit (-e --eval) lets you evaluate an expression and exit without entering REPL mode; Imports by -i --import are performed before -e --eval so they can be combined
```
--eval EVAL, -e EVAL   evaluate expression and exit

> abacus -e "5+5"
10
```

All common operations

> 1+1
2
> 1-20
-19
> 5^0 / 20
0.05
> 2**(2+5)
128
> 10%
0.10
> 10 %% 3    # modulo operator
1

Variables

> d = 12.5
12.5
> d * 5 + 5
67.5
> a * 5 + 5
5

Note: Undefined variables are equal to 0

Last answers are saved in the variables ans and answer by default
```
> 4**5
1024
> ans
1024
```

Comparisons <, ==, >, <=, >=

> pi > phi
true
> 10 <=10
true
> 2 == 0
false

E, Pi, Phi

> e
2.7182818284590450907955982984276
> pi
3.1415926535897931159979634685442
> phi
1.6180339887498949025257388711907

Single arity functions:
- sqrt, cbrt, ln, log, log2, log10, floor, ceil, exp, sin, cos, tan, abs, round
Two arity functions (accept 2-tuples):
- round (number, digits of precision)
```
> round(1.123456789,4)
1.123
```
- log (number, base)
```
> log(16,4)
2
```

N-arity functions (accept n-tuples):

min, max, avg, from, until, reverse, nth

> d, f = 10, 20
(10, 20)
> min(d, 4, -1, f, 0, 2)
-1
> max(d, 4, -1, f, 0, 2)
20
> avg(d, 4, -1, f, 0, 2)
5.8333..

> Map__ = value,Fn -> Fn(value), Map__(value+1, Fn)
> List = start, len, Fn -> until(Map__(start, Fn)[rec: len], len)
> I = x -> x
> List(1, 5, I)
(1, 2, 3, 4, 5)

> from(List(1, 5, I), 2)
(3, 4, 5)
> until(List(1, 5, I), 2)
(1, 2)
> nth(List(1, 5, I), 2)
3
> reverse(List(1, 5, I))
(5, 4, 3, 2, 1)

Note: from(List(1, 5, I), 2) is equivalent to from(1,2,3,4,5,2)

Reserved names

quit – If a query includes quit, the program will terminate and the query will not be saved to the history file
ans and answer – variables always contain the last computed numeric value (can be overriden with the --answer-vars argument)
The constants e, pi, and phi

Lambda expression support

Defining lambdas

<LambdaName> = <arguments> -> <expression>   // or
<LambdaName> = (<arguments>) => <expression> // or
<LambdaName> = <arguments> -> <expression>, <expression>, ...

Both variables and lambda placeholders/aliases can be provided as arguments:

Identity = x -> x
RunFnOnX = x, Fn -> Fn(x)

Note:

Lambda names begin with a capital letter
Parentheses around the arguments are optional, except when no variables are to be provided, e.g. F = () -> 5+5
Lambdas can return multiple values - a tuple.
Both -> and => can be used between the lambda variables and the expressions tuple.

Examples

Identity = x -> x
RunFnOnX = x, Fn -> Fn(x)
Area = a, b => a*b
Hypothenuse = (a,b) -> sqrt(a**2+b**2)
ToRad = deg -> deg * pi / 180

Calling lambdas

<LambdaName>(<parameters>)

Examples

> Identity = x -> x
> Identity(2)
2
> Identity()
expected 1 parameter
> UndefinedLambda()
0

Note:

undefined lambdas return 0 by default like undefined variables

Arguments and recursion

Lambdas can use global variables and constants and will default to global variables if a variable in the lambda expression isn't in the arguments tuple. The same applies to lambda aliases.

> Add = x, y -> (x + y) * not_found
> Add(5, 6)
0
> not_found = 1
> Add(5, 6)
11

> ApplyFn = x, Fn -> Fn(x)
> ApplyFn(12, Test)
0
> Test = x -> x*2
> ApplyFn(12, Test)
24

Lambdas can be recursive but only if explicitly told when called.

> Factorial = x -> x * Factorial(x - 1)
> Factorial(10)
recursion is disabled

To specify recursion parameters use [] after the lambda call.

F(value)[rec=10, last=x*10, stop=x < 5, mem: false]

rec — Expression (evaluated globally), Default: 0
- specifies the maximum number of times the lambda can call itself during the evaluation of the current expression;
last — Expression (evaluated by the lambda), Default: 0
- specifies the expression which the last lambda automatically evalates when rec is reached or when stop is true;
stop — BoolExpression (evaluated by the lambda)
- a boolean expression which can use the lambda's variables; if true, the lambda returns last and stops recurring;
mem — BoolExpression (evaluated globally), Default: false
- whether or not to utilize memoization for the current expression (useful when using recursion).

Either = or : may be used between the parameter name and the value.

> Factorial(10)[rec: 10]
0
> Factorial(10)[rec:10, last=1]
3628800 
> Factorial(10)[rec:10, last:1, stop: x == 5]
30240  // 10 × 9 × 8 × 7 × 6

What exactly is happening?

If we define a new lambda Count = x -> x,Count(x-1) which returns a tuple we can observe how the value of x changes.

> Count(10)[rec:10]
(10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0)

> Count(10)[rec:10, last:100]
(10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 100)

> Count(10)[rec:4, last:x*5]
(10, 9, 8, 7, 30)

>  Count(10)[rec:10, last:x, stop: x == 5]
(10, 9, 8, 7, 6, 5)

Advanced example with memoization and `until`, `from`, `reverse`, and `nth`

> Fib = x -> Fib(x-1) + Fib(x-2)
> Map_ = value -> Fn(value), Map_(value-1)
> Map = value,length->Map_(value)[rec:length-1,last:Fn(value)]
> Fn = x -> Fib(x)[rec:1e6,last:1,stop:x<3]
> Map(10,10)
(55, 34, 21, 13, 8, 5, 3, 2, 1, 1)

> until(Map(10,10), 5)
(55, 34, 21, 13, 8)

> reverse(Map(10,10))
(1, 1, 2, 3, 5, 8, 13, 21, 34, 55)

> from(reverse(Map(10,10)), 1)
(1, 2, 3, 5, 8, 13, 21, 34, 55)

> from(reverse(Map(10,10)), 5)
(8, 13, 21, 34, 55)

> nth(from(reverse(Map(10,10)),5),2)
21


// If we attempted Map(20,10) it would take a while to compute because
Fib(20) branches out 2^n times.

> Map(20,10)
(6765, 4181, 2584, 1597, 987, 610, 377, 233, 144, 89)

// But due to the nature of the recursive Fibonacci algorithm, a lot
of the same function calls are made which means we can drammatically
speed up execution by caching computations.
> Fn = x -> Fib(x)[rec:1e6, last:1, stop:x<3, mem: true]
> Map(200,1)
280571172992510140037611932413038677189525

// Try it for yourself

TODO

Add full feature list
Write tests
- Base tests
- Simple benchmark of a complicated expression
- Improve tests
Refactor to depend less on other packages
Implement most single arity functions with *big.Float for improved precision

viktordanov/abacus

🧮 Abacus

Install

Arch Linux

Manually

Features

Reserved names

Lambda expression support

Defining lambdas

Examples

Calling lambdas

Examples

Arguments and recursion

What exactly is happening?

Advanced example with memoization and until, from, reverse, and nth

TODO

Advanced example with memoization and `until`, `from`, `reverse`, and `nth`