/pyod

A Comprehensive and Scalable Python Library for Outlier Detection (Anomaly Detection)

Primary LanguagePythonBSD 2-Clause "Simplified" LicenseBSD-2-Clause

Python Outlier Detection (PyOD)

Deployment & Documentation & Stats & License

PyPI version Anaconda version Documentation status GitHub stars GitHub forks Downloads testing Coverage Status Maintainability License

PyOD is the most comprehensive and scalable Python toolkit for detecting outlying objects in multivariate data. This exciting yet challenging field is commonly referred as Outlier Detection or Anomaly Detection.

PyOD includes more than 40 detection algorithms, from classical LOF (SIGMOD 2000) to the latest ECOD (TKDE 2022). Since 2017, PyOD has been successfully used in numerous academic researches and commercial products [39] [40] with more than 6 million downloads. It is also well acknowledged by the machine learning community with various dedicated posts/tutorials, including Analytics Vidhya, KDnuggets, Towards Data Science, and awesome-machine-learning.

PyOD is featured for:

  • Unified APIs, detailed documentation, and interactive examples across various algorithms.
  • Advanced models, including classical ones by distance and density estimation, latest deep learning methods, and emerging algorithms like ECOD.
  • Optimized performance with JIT and parallelization using numba and joblib.
  • Fast training & prediction with SUOD [40].

Outlier Detection with 5 Lines of Code:

# train an ECOD detector
from pyod.models.ecod import ECOD
clf = ECOD()
clf.fit(X_train)

# get outlier scores
y_train_scores = clf.decision_scores_  # raw outlier scores on the train data
y_test_scores = clf.decision_function(X_test)  # predict raw outlier scores on test

Citing PyOD:

PyOD paper is published in Journal of Machine Learning Research (JMLR) (MLOSS track). If you use PyOD in a scientific publication, we would appreciate citations to the following paper:

@article{zhao2019pyod,
  author  = {Zhao, Yue and Nasrullah, Zain and Li, Zheng},
  title   = {PyOD: A Python Toolbox for Scalable Outlier Detection},
  journal = {Journal of Machine Learning Research},
  year    = {2019},
  volume  = {20},
  number  = {96},
  pages   = {1-7},
  url     = {http://jmlr.org/papers/v20/19-011.html}
}

or:

Zhao, Y., Nasrullah, Z. and Li, Z., 2019. PyOD: A Python Toolbox for Scalable Outlier Detection. Journal of machine learning research (JMLR), 20(96), pp.1-7.

Key Links and Resources:

Table of Contents:

Installation

It is recommended to use pip or conda for installation. Please make sure the latest version is installed, as PyOD is updated frequently:

pip install pyod            # normal install
pip install --upgrade pyod  # or update if needed
conda install -c conda-forge pyod

Alternatively, you could clone and run setup.py file:

git clone https://github.com/yzhao062/pyod.git
cd pyod
pip install .

Required Dependencies:

  • Python 3.6+
  • combo>=0.1.3
  • joblib
  • numpy>=1.19
  • numba>=0.51
  • scipy>=1.5.1
  • scikit_learn>=0.20.0
  • six
  • statsmodels

Optional Dependencies (see details below):

  • combo (optional, required for models/combination.py and FeatureBagging)
  • keras/tensorflow (optional, required for AutoEncoder, and other deep learning models)
  • matplotlib (optional, required for running examples)
  • pandas (optional, required for running benchmark)
  • suod (optional, required for running SUOD model)
  • xgboost (optional, required for XGBOD)

Warning 1: PyOD has multiple neural network based models, e.g., AutoEncoders, which are implemented in both PyTorch and Tensorflow. However, PyOD does NOT install DL libraries for you. This reduces the risk of interfering with your local copies. If you want to use neural-net based models, please make sure Keras and a backend library, e.g., TensorFlow, are installed. Instructions are provided: neural-net FAQ. Similarly, models depending on xgboost, e.g., XGBOD, would NOT enforce xgboost installation by default.

Warning 2: PyOD contains multiple models that also exist in scikit-learn. However, these two libraries' API is not exactly the same--it is recommended to use only one of them for consistency but not mix the results. Refer Differences between scikit-learn and PyOD for more information.

API Cheatsheet & Reference

Full API Reference: (https://pyod.readthedocs.io/en/latest/pyod.html). API cheatsheet for all detectors:

  • fit(X): Fit detector. y is ignored in unsupervised methods.
  • decision_function(X): Predict raw anomaly score of X using the fitted detector.
  • predict(X): Predict if a particular sample is an outlier or not using the fitted detector.
  • predict_proba(X): Predict the probability of a sample being outlier using the fitted detector.
  • predict_confidence(X): Predict the model's sample-wise confidence (available in predict and predict_proba) [29].

Key Attributes of a fitted model:

  • decision_scores_: The outlier scores of the training data. The higher, the more abnormal. Outliers tend to have higher scores.
  • labels_: The binary labels of the training data. 0 stands for inliers and 1 for outliers/anomalies.

Model Save & Load

PyOD takes a similar approach of sklearn regarding model persistence. See model persistence for clarification.

In short, we recommend to use joblib or pickle for saving and loading PyOD models. See "examples/save_load_model_example.py" for an example. In short, it is simple as below:

from joblib import dump, load

# save the model
dump(clf, 'clf.joblib')
# load the model
clf = load('clf.joblib')

It is known that there are challenges in saving neural network models. Check #328 and #88 for temporary workaround.

Fast Train with SUOD

Fast training and prediction: it is possible to train and predict with a large number of detection models in PyOD by leveraging SUOD framework [40]. See SUOD Paper and SUOD example.

from pyod.models.suod import SUOD

# initialized a group of outlier detectors for acceleration
detector_list = [LOF(n_neighbors=15), LOF(n_neighbors=20),
                 LOF(n_neighbors=25), LOF(n_neighbors=35),
                 COPOD(), IForest(n_estimators=100),
                 IForest(n_estimators=200)]

# decide the number of parallel process, and the combination method
# then clf can be used as any outlier detection model
clf = SUOD(base_estimators=detector_list, n_jobs=2, combination='average',
           verbose=False)

Implemented Algorithms

PyOD toolkit consists of three major functional groups:

(i) Individual Detection Algorithms :

Type Abbr Algorithm Year Ref
Probabilistic ECOD Unsupervised Outlier Detection Using Empirical Cumulative Distribution Functions 2022 [24]
Probabilistic ABOD Angle-Based Outlier Detection 2008 [18]
Probabilistic FastABOD Fast Angle-Based Outlier Detection using approximation 2008 [18]
Probabilistic COPOD COPOD: Copula-Based Outlier Detection 2020 [23]
Probabilistic MAD Median Absolute Deviation (MAD) 1993 [15]
Probabilistic SOS Stochastic Outlier Selection 2012 [16]
Probabilistic KDE Outlier Detection with Kernel Density Functions 2007 [20]
Probabilistic Sampling Rapid distance-based outlier detection via sampling 2013 [35]
Linear Model PCA Principal Component Analysis (the sum of weighted projected distances to the eigenvector hyperplanes) 2003 [34]
Linear Model MCD Minimum Covariance Determinant (use the mahalanobis distances as the outlier scores) 1999 [13] [31]
Linear Model CD Use Cook's distance for outlier detection 1977 [10]
Linear Model OCSVM One-Class Support Vector Machines 2001 [33]
Linear Model LMDD Deviation-based Outlier Detection (LMDD) 1996 [6]
Proximity-Based LOF Local Outlier Factor 2000 [8]
Proximity-Based COF Connectivity-Based Outlier Factor 2002 [36]
Proximity-Based (Incremental) COF Memory Efficient Connectivity-Based Outlier Factor (slower but reduce storage complexity) 2002 [36]
Proximity-Based CBLOF Clustering-Based Local Outlier Factor 2003 [14]
Proximity-Based LOCI LOCI: Fast outlier detection using the local correlation integral 2003 [27]
Proximity-Based HBOS Histogram-based Outlier Score 2012 [11]
Proximity-Based kNN k Nearest Neighbors (use the distance to the kth nearest neighbor as the outlier score) 2000 [30]
Proximity-Based AvgKNN Average kNN (use the average distance to k nearest neighbors as the outlier score) 2002 [5]
Proximity-Based MedKNN Median kNN (use the median distance to k nearest neighbors as the outlier score) 2002 [5]
Proximity-Based SOD Subspace Outlier Detection 2009 [19]
Proximity-Based ROD Rotation-based Outlier Detection 2020 [4]
Outlier Ensembles IForest Isolation Forest 2008 [25]
Outlier Ensembles INNE Isolation-based Anomaly Detection Using Nearest-Neighbor Ensembles 2018 [7]
Outlier Ensembles FB Feature Bagging 2005 [21]
Outlier Ensembles LSCP LSCP: Locally Selective Combination of Parallel Outlier Ensembles 2019 [39]
Outlier Ensembles XGBOD Extreme Boosting Based Outlier Detection (Supervised) 2018 [38]
Outlier Ensembles LODA Lightweight On-line Detector of Anomalies 2016 [28]
Outlier Ensembles SUOD SUOD: Accelerating Large-scale Unsupervised Heterogeneous Outlier Detection (Acceleration) 2021 [40]
Neural Networks AutoEncoder Fully connected AutoEncoder (use reconstruction error as the outlier score)   [1] [Ch.3]
Neural Networks VAE Variational AutoEncoder (use reconstruction error as the outlier score) 2013 [17]
Neural Networks Beta-VAE Variational AutoEncoder (all customized loss term by varying gamma and capacity) 2018 [9]
Neural Networks SO_GAAL Single-Objective Generative Adversarial Active Learning 2019 [26]
Neural Networks MO_GAAL Multiple-Objective Generative Adversarial Active Learning 2019 [26]
Neural Networks DeepSVDD Deep One-Class Classification 2018 [32]

(ii) Outlier Ensembles & Outlier Detector Combination Frameworks:

Type Abbr Algorithm Year Ref
Outlier Ensembles FB Feature Bagging 2005 [21]
Outlier Ensembles LSCP LSCP: Locally Selective Combination of Parallel Outlier Ensembles 2019 [39]
Outlier Ensembles XGBOD Extreme Boosting Based Outlier Detection (Supervised) 2018 [38]
Outlier Ensembles LODA Lightweight On-line Detector of Anomalies 2016 [28]
Outlier Ensembles SUOD SUOD: Accelerating Large-scale Unsupervised Heterogeneous Outlier Detection (Acceleration) 2021 [40]
Outlier Ensembles INNE Isolation-based Anomaly Detection Using Nearest-Neighbor Ensembles 2018 [7]
Combination Average Simple combination by averaging the scores 2015 [2]
Combination Weighted Average Simple combination by averaging the scores with detector weights 2015 [2]
Combination Maximization Simple combination by taking the maximum scores 2015 [2]
Combination AOM Average of Maximum 2015 [2]
Combination MOA Maximization of Average 2015 [2]
Combination Median Simple combination by taking the median of the scores 2015 [2]
Combination majority Vote Simple combination by taking the majority vote of the labels (weights can be used) 2015 [2]

(iii) Utility Functions:

Type Name Function Documentation
Data generate_data Synthesized data generation; normal data is generated by a multivariate Gaussian and outliers are generated by a uniform distribution generate_data
Data generate_data_clusters Synthesized data generation in clusters; more complex data patterns can be created with multiple clusters generate_data_clusters
Stat wpearsonr Calculate the weighted Pearson correlation of two samples wpearsonr
Utility get_label_n Turn raw outlier scores into binary labels by assign 1 to top n outlier scores get_label_n
Utility precision_n_scores calculate precision @ rank n precision_n_scores

Algorithm Benchmark

The comparison among of implemented models is made available below (Figure, compare_all_models.py, Interactive Jupyter Notebooks). For Jupyter Notebooks, please navigate to "/notebooks/Compare All Models.ipynb".

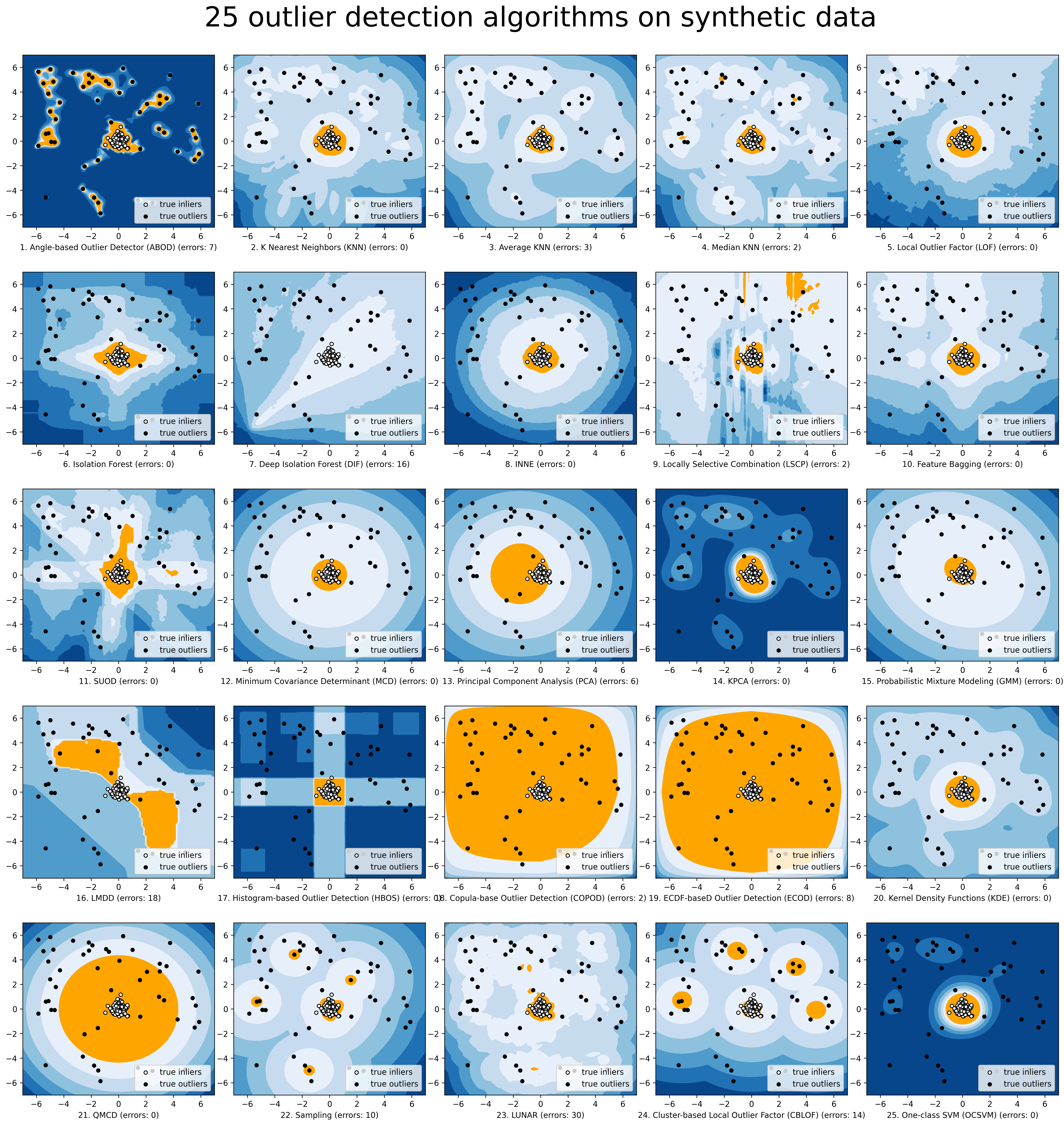
Comparision_of_All

A benchmark is supplied for select algorithms to provide an overview of the implemented models. In total, 17 benchmark datasets are used for comparison, which can be downloaded at ODDS.

For each dataset, it is first split into 60% for training and 40% for testing. All experiments are repeated 10 times independently with random splits. The mean of 10 trials is regarded as the final result. Three evaluation metrics are provided:

  • The area under receiver operating characteristic (ROC) curve
  • Precision @ rank n (P@N)
  • Execution time

Check the latest benchmark. You could replicate this process by running benchmark.py.

Quick Start for Outlier Detection

PyOD has been well acknowledged by the machine learning community with a few featured posts and tutorials.

Analytics Vidhya: An Awesome Tutorial to Learn Outlier Detection in Python using PyOD Library

KDnuggets: Intuitive Visualization of Outlier Detection Methods, An Overview of Outlier Detection Methods from PyOD

Towards Data Science: Anomaly Detection for Dummies

Computer Vision News (March 2019): Python Open Source Toolbox for Outlier Detection

"examples/knn_example.py" demonstrates the basic API of using kNN detector. It is noted that the API across all other algorithms are consistent/similar.

More detailed instructions for running examples can be found in examples directory.

  1. Initialize a kNN detector, fit the model, and make the prediction.

    from pyod.models.knn import KNN   # kNN detector

# train kNN detector
clf_name = 'KNN'
clf = KNN()
clf.fit(X_train)

# get the prediction label and outlier scores of the training data
y_train_pred = clf.labels_  # binary labels (0: inliers, 1: outliers)
y_train_scores = clf.decision_scores_  # raw outlier scores

# get the prediction on the test data
y_test_pred = clf.predict(X_test)  # outlier labels (0 or 1)
y_test_scores = clf.decision_function(X_test)  # outlier scores

# it is possible to get the prediction confidence as well
y_test_pred, y_test_pred_confidence = clf.predict(X_test, return_confidence=True)  # outlier labels (0 or 1) and confidence in the range of [0,1]

  2. Evaluate the prediction by ROC and Precision @ Rank n (p@n).

    from pyod.utils.data import evaluate_print

# evaluate and print the results
print("\nOn Training Data:")
evaluate_print(clf_name, y_train, y_train_scores)
print("\nOn Test Data:")
evaluate_print(clf_name, y_test, y_test_scores)

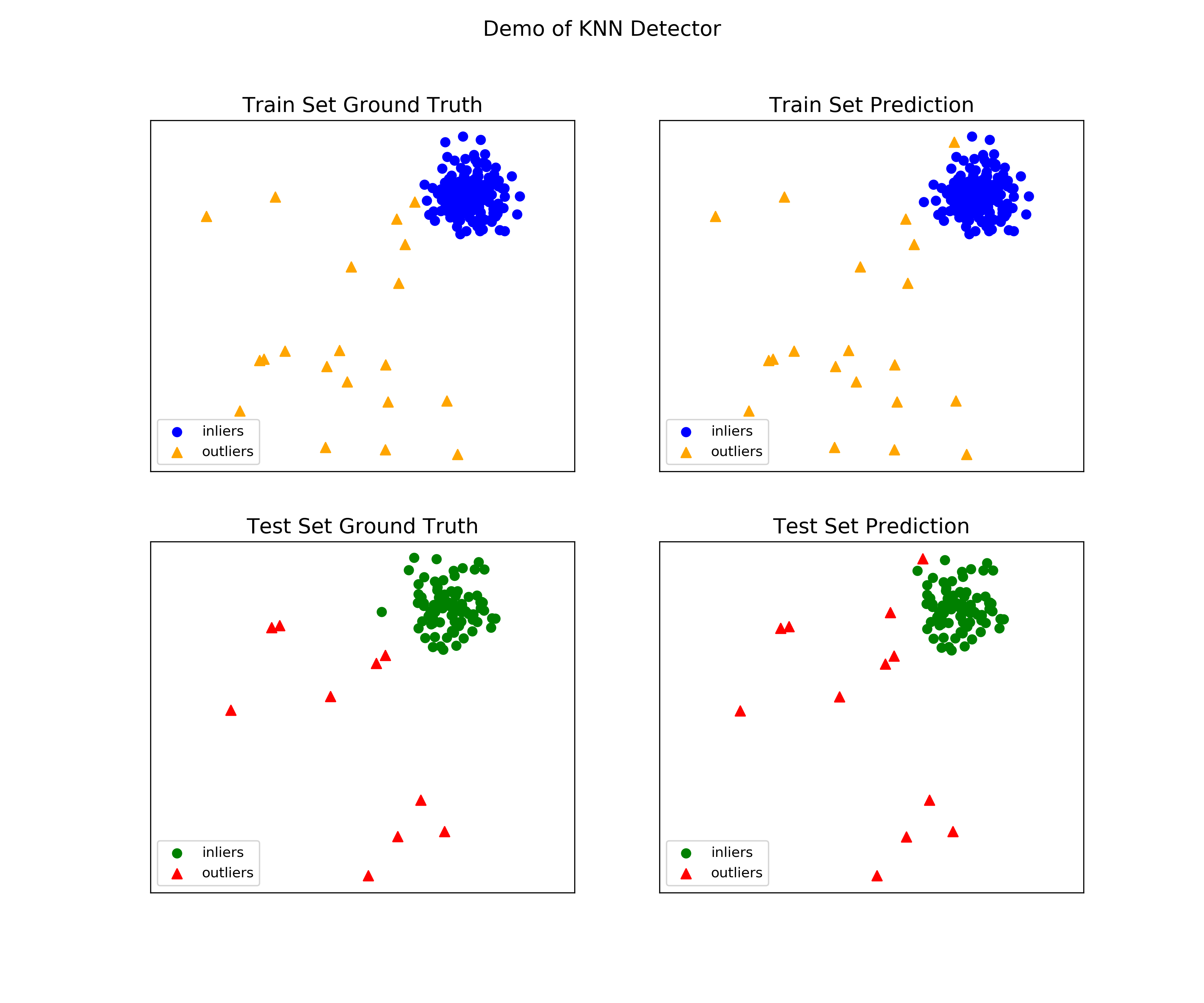
  3. See a sample output & visualization.

    On Training Data:
KNN ROC:1.0, precision @ rank n:1.0

On Test Data:
KNN ROC:0.9989, precision @ rank n:0.9
    visualize(clf_name, X_train, y_train, X_test, y_test, y_train_pred,
    y_test_pred, show_figure=True, save_figure=False)

Visualization (knn_figure):

kNN example figure

How to Contribute

You are welcome to contribute to this exciting project:

  • Please first check Issue lists for "help wanted" tag and comment the one you are interested. We will assign the issue to you.
  • Fork the master branch and add your improvement/modification/fix.
  • Create a pull request to development branch and follow the pull request template PR template
  • Automatic tests will be triggered. Make sure all tests are passed. Please make sure all added modules are accompanied with proper test functions.

To make sure the code has the same style and standard, please refer to abod.py, hbos.py, or feature_bagging.py for example.

You are also welcome to share your ideas by opening an issue or dropping me an email at zhaoy@cmu.edu :)

Inclusion Criteria

Similarly to scikit-learn, We mainly consider well-established algorithms for inclusion. A rule of thumb is at least two years since publication, 50+ citations, and usefulness.

However, we encourage the author(s) of newly proposed models to share and add your implementation into PyOD for boosting ML accessibility and reproducibility. This exception only applies if you could commit to the maintenance of your model for at least two year period.

Reference

[1]Aggarwal, C.C., 2015. Outlier analysis. In Data mining (pp. 237-263). Springer, Cham.
[2](1, 2, 3, 4, 5, 6, 7) Aggarwal, C.C. and Sathe, S., 2015. Theoretical foundations and algorithms for outlier ensembles.ACM SIGKDD Explorations Newsletter, 17(1), pp.24-47.
[3]Aggarwal, C.C. and Sathe, S., 2017. Outlier ensembles: An introduction. Springer.
[4]Almardeny, Y., Boujnah, N. and Cleary, F., 2020. A Novel Outlier Detection Method for Multivariate Data. IEEE Transactions on Knowledge and Data Engineering.
[5](1, 2) Angiulli, F. and Pizzuti, C., 2002, August. Fast outlier detection in high dimensional spaces. In European Conference on Principles of Data Mining and Knowledge Discovery pp. 15-27.
[6]Arning, A., Agrawal, R. and Raghavan, P., 1996, August. A Linear Method for Deviation Detection in Large Databases. In KDD (Vol. 1141, No. 50, pp. 972-981).
[7](1, 2) Bandaragoda, T. R., Ting, K. M., Albrecht, D., Liu, F. T., Zhu, Y., and Wells, J. R., 2018, Isolation-based anomaly detection using nearest-neighbor ensembles. Computational Intelligence, 34(4), pp. 968-998.
[8]Breunig, M.M., Kriegel, H.P., Ng, R.T. and Sander, J., 2000, May. LOF: identifying density-based local outliers. ACM Sigmod Record, 29(2), pp. 93-104.
[9]Burgess, Christopher P., et al. "Understanding disentangling in beta-VAE." arXiv preprint arXiv:1804.03599 (2018).
[10]Cook, R.D., 1977. Detection of influential observation in linear regression. Technometrics, 19(1), pp.15-18.
[11]Goldstein, M. and Dengel, A., 2012. Histogram-based outlier score (hbos): A fast unsupervised anomaly detection algorithm. In KI-2012: Poster and Demo Track, pp.59-63.
[12]Gopalan, P., Sharan, V. and Wieder, U., 2019. PIDForest: Anomaly Detection via Partial Identification. In Advances in Neural Information Processing Systems, pp. 15783-15793.
[13]Hardin, J. and Rocke, D.M., 2004. Outlier detection in the multiple cluster setting using the minimum covariance determinant estimator. Computational Statistics & Data Analysis, 44(4), pp.625-638.
[14]He, Z., Xu, X. and Deng, S., 2003. Discovering cluster-based local outliers. Pattern Recognition Letters, 24(9-10), pp.1641-1650.
[15]Iglewicz, B. and Hoaglin, D.C., 1993. How to detect and handle outliers (Vol. 16). Asq Press.
[16]Janssens, J.H.M., Huszár, F., Postma, E.O. and van den Herik, H.J., 2012. Stochastic outlier selection. Technical report TiCC TR 2012-001, Tilburg University, Tilburg Center for Cognition and Communication, Tilburg, The Netherlands.
[17]Kingma, D.P. and Welling, M., 2013. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
[18](1, 2) Kriegel, H.P. and Zimek, A., 2008, August. Angle-based outlier detection in high-dimensional data. In KDD '08, pp. 444-452. ACM.
[19]Kriegel, H.P., Kröger, P., Schubert, E. and Zimek, A., 2009, April. Outlier detection in axis-parallel subspaces of high dimensional data. In Pacific-Asia Conference on Knowledge Discovery and Data Mining, pp. 831-838. Springer, Berlin, Heidelberg.
[20]Latecki, L.J., Lazarevic, A. and Pokrajac, D., 2007, July. Outlier detection with kernel density functions. In International Workshop on Machine Learning and Data Mining in Pattern Recognition (pp. 61-75). Springer, Berlin, Heidelberg.
[21](1, 2) Lazarevic, A. and Kumar, V., 2005, August. Feature bagging for outlier detection. In KDD '05. 2005.
[22]Li, D., Chen, D., Jin, B., Shi, L., Goh, J. and Ng, S.K., 2019, September. MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks. In International Conference on Artificial Neural Networks (pp. 703-716). Springer, Cham.
[23]Li, Z., Zhao, Y., Botta, N., Ionescu, C. and Hu, X. COPOD: Copula-Based Outlier Detection. IEEE International Conference on Data Mining (ICDM), 2020.
[24]Li, Z., Zhao, Y., Hu, X., Botta, N., Ionescu, C. and Chen, H. G. ECOD: Unsupervised Outlier Detection Using Empirical Cumulative Distribution Functions. IEEE Transactions on Knowledge and Data Engineering (TKDE), 2022.
[25]Liu, F.T., Ting, K.M. and Zhou, Z.H., 2008, December. Isolation forest. In International Conference on Data Mining, pp. 413-422. IEEE.
[26](1, 2) Liu, Y., Li, Z., Zhou, C., Jiang, Y., Sun, J., Wang, M. and He, X., 2019. Generative adversarial active learning for unsupervised outlier detection. IEEE Transactions on Knowledge and Data Engineering.
[27]Papadimitriou, S., Kitagawa, H., Gibbons, P.B. and Faloutsos, C., 2003, March. LOCI: Fast outlier detection using the local correlation integral. In ICDE '03, pp. 315-326. IEEE.
[28](1, 2) Pevný, T., 2016. Loda: Lightweight on-line detector of anomalies. Machine Learning, 102(2), pp.275-304.
[29]Perini, L., Vercruyssen, V., Davis, J. Quantifying the confidence of anomaly detectors in their example-wise predictions. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases (ECML-PKDD), 2020.
[30]Ramaswamy, S., Rastogi, R. and Shim, K., 2000, May. Efficient algorithms for mining outliers from large data sets. ACM Sigmod Record, 29(2), pp. 427-438.
[31]Rousseeuw, P.J. and Driessen, K.V., 1999. A fast algorithm for the minimum covariance determinant estimator. Technometrics, 41(3), pp.212-223.
[32]Ruff, L., Vandermeulen, R., Goernitz, N., Deecke, L., Siddiqui, S.A., Binder, A., Müller, E. and Kloft, M., 2018, July. Deep one-class classification. In International conference on machine learning (pp. 4393-4402). PMLR.
[33]Scholkopf, B., Platt, J.C., Shawe-Taylor, J., Smola, A.J. and Williamson, R.C., 2001. Estimating the support of a high-dimensional distribution. Neural Computation, 13(7), pp.1443-1471.
[34]Shyu, M.L., Chen, S.C., Sarinnapakorn, K. and Chang, L., 2003. A novel anomaly detection scheme based on principal component classifier. MIAMI UNIV CORAL GABLES FL DEPT OF ELECTRICAL AND COMPUTER ENGINEERING.
[35]Sugiyama, M. and Borgwardt, K., 2013. Rapid distance-based outlier detection via sampling. Advances in neural information processing systems, 26.
[36](1, 2) Tang, J., Chen, Z., Fu, A.W.C. and Cheung, D.W., 2002, May. Enhancing effectiveness of outlier detections for low density patterns. In Pacific-Asia Conference on Knowledge Discovery and Data Mining, pp. 535-548. Springer, Berlin, Heidelberg.
[37]Wang, X., Du, Y., Lin, S., Cui, P., Shen, Y. and Yang, Y., 2019. adVAE: A self-adversarial variational autoencoder with Gaussian anomaly prior knowledge for anomaly detection. Knowledge-Based Systems.
[38](1, 2) Zhao, Y. and Hryniewicki, M.K. XGBOD: Improving Supervised Outlier Detection with Unsupervised Representation Learning. IEEE International Joint Conference on Neural Networks, 2018.
[39](1, 2, 3) Zhao, Y., Nasrullah, Z., Hryniewicki, M.K. and Li, Z., 2019, May. LSCP: Locally selective combination in parallel outlier ensembles. In Proceedings of the 2019 SIAM International Conference on Data Mining (SDM), pp. 585-593. Society for Industrial and Applied Mathematics.
[40](1, 2, 3, 4, 5) Zhao, Y., Hu, X., Cheng, C., Wang, C., Wan, C., Wang, W., Yang, J., Bai, H., Li, Z., Xiao, C., Wang, Y., Qiao, Z., Sun, J. and Akoglu, L. (2021). SUOD: Accelerating Large-scale Unsupervised Heterogeneous Outlier Detection. Conference on Machine Learning and Systems (MLSys).