Python package containing tools for radial basis function (RBF) applications. Applications include interpolating/smoothing scattered data and solving PDEs over irregular domains. This package was heavily influenced by the books "Meshfree Approximation Methods with Matlab" by Gregory Fasshauer and "A Primer on Radial Basis Functions with Applications to the Geosciences" by Bengt Fornberg and Natasha Flyer. The complete documentation for this package can be found here.
- Functions for evaluating RBFs and their exact derivatives.
- A class for RBF interpolation, which is used for interpolating and smoothing scattered, noisy, N-dimensional data.
- An algorithm for generating Radial Basis Function Finite Difference (RBF-FD) weights. This is used for solving large scale PDEs over irregular domains.
- A node generation algorithm which can be used for solving PDEs with the spectral RBF method or the RBF-FD method.
- An abstraction for Gaussian processes. Gaussian processes are primarily used here for Gaussian process regression (GPR), which is a nonparametric Bayesian interpolation/smoothing method.
- Halton sequence generator.
- Computational geometry functions (e.g. point in polygon testing) for two and three spatial dimensions.
RBF requires the following python packages: numpy, scipy, sympy, cython, and rtree. These dependencies should be satisfied with just the base Anaconda python package (https://www.continuum.io/downloads)
download the RBF package
$ git clone http://github.com/treverhines/RBF.gitcompile and install
$ cd RBF
$ python setup.py installtest that everything works
$ cd test
$ python -m unittest discover'''
In this example we generate synthetic scattered data with added
noise and then fit it with a smoothed RBF interpolant. The
interpolant in this example is equivalent to a thin plate spline.
'''
import numpy as np
from rbf.interpolate import RBFInterpolant
import matplotlib.pyplot as plt
np.random.seed(1)
# observation points
x_obs = np.random.random((100, 2))
# values at the observation points
u_obs = np.sin(2*np.pi*x_obs[:, 0])*np.cos(2*np.pi*x_obs[:, 1])
u_obs += np.random.normal(0.0, 0.1, 100)
# create a thin-plate spline interpolant, where the data is assumed
# to be noisy
I = RBFInterpolant(x_obs, u_obs, sigma=0.1, phi='phs2', order=1)
# create the interpolation points, and evaluate the interpolant
x1, x2 = np.linspace(0, 1, 200), np.linspace(0, 1, 200)
x_itp = np.reshape(np.meshgrid(x1, x2), (2, 200*200)).T
u_itp = I(x_itp)
# plot the results
plt.tripcolor(x_itp[:, 0], x_itp[:, 1], u_itp, vmin=-1.1, vmax=1.1, cmap='viridis')
plt.scatter(x_obs[:, 0], x_obs[:, 1], s=100, c=u_obs, vmin=-1.1, vmax=1.1,
cmap='viridis', edgecolor='k')
plt.xlim((0.05, 0.95))
plt.ylim((0.05, 0.95))
plt.colorbar()
plt.tight_layout()
plt.show()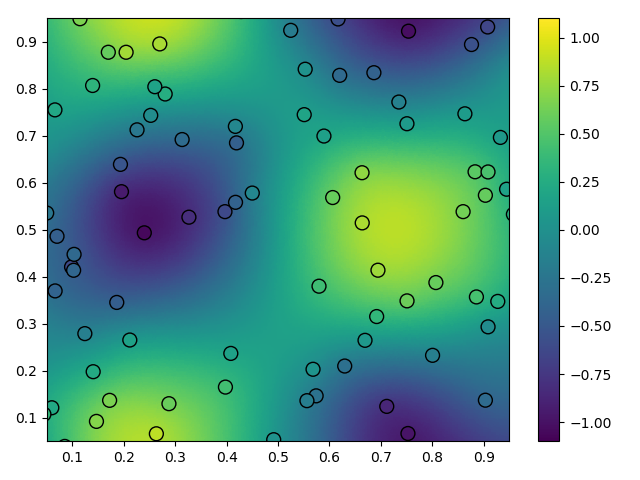
Plot generated by the above code. Observations are shown as scatter points and the smoothed interpolant is the color field.
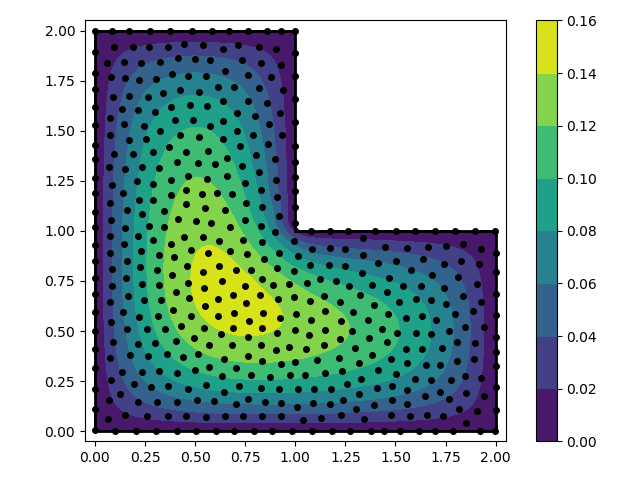
There are two methods for solving PDEs with RBFs: the spectral method and the RBF-FD method. The spectral method has been touted as having remarkable accuracy; however it is only applicable for small scale problems and requires a good choice for a shape parameter. The RBF-FD method is appealing because it can be used for large scale problems, there is no need to tune a shape parameter (assuming you use polyharmonic splines to generate the weights), and higher order accuracy can be attained by simply increasing the stencil size or increasing the order of the polynomial used to generate the weights. In short, the RBF-FD method should always be preferred over the spectral RBF method. An example of the two methods is provided below.
'''
In this example we solve the Poisson equation over an L-shaped
domain with fixed boundary conditions. We use the multiquadratic RBF
(`mq`)
'''
import numpy as np
from rbf.basis import mq
from rbf.pde.geometry import contains
from rbf.pde.nodes import poisson_disc_nodes
import matplotlib.pyplot as plt
# Define the problem domain with line segments.
vert = np.array([[0.0, 0.0], [2.0, 0.0], [2.0, 1.0],
[1.0, 1.0], [1.0, 2.0], [0.0, 2.0]])
smp = np.array([[0, 1], [1, 2], [2, 3], [3, 4], [4, 5], [5, 0]])
spacing = 0.07 # approximate spacing between nodes
eps = 0.3/spacing # shape parameter
# generate the nodes. `nodes` is a (N, 2) float array, `groups` is a
# dict identifying which group each node is in
nodes, groups, _ = poisson_disc_nodes(spacing, (vert, smp))
N = nodes.shape[0]
# create "left hand side" matrix
A = np.empty((N, N))
A[groups['interior']] = mq(nodes[groups['interior']], nodes, eps=eps, diff=[2, 0])
A[groups['interior']] += mq(nodes[groups['interior']], nodes, eps=eps, diff=[0, 2])
A[groups['boundary:all']] = mq(nodes[groups['boundary:all']], nodes, eps=eps)
# create "right hand side" vector
d = np.empty(N)
d[groups['interior']] = -1.0 # forcing term
d[groups['boundary:all']] = 0.0 # boundary condition
# Solve for the RBF coefficients
coeff = np.linalg.solve(A, d)
# interpolate the solution on a grid
xg, yg = np.meshgrid(np.linspace(0.0, 2.02, 100),
np.linspace(0.0, 2.02, 100))
points = np.array([xg.flatten(), yg.flatten()]).T
u = mq(points, nodes, eps=eps).dot(coeff)
# mask points outside of the domain
u[~contains(points, vert, smp)] = np.nan
# fold the solution into a grid
ug = u.reshape((100, 100))
# make a contour plot of the solution
fig, ax = plt.subplots()
p = ax.contourf(xg, yg, ug, np.linspace(0.0, 0.16, 9), cmap='viridis')
ax.plot(nodes[:, 0], nodes[:, 1], 'ko', markersize=4)
for s in smp:
ax.plot(vert[s, 0], vert[s, 1], 'k-', lw=2)
ax.set_aspect('equal')
ax.set_xlim(-0.05, 2.05)
ax.set_ylim(-0.05, 2.05)
fig.colorbar(p, ax=ax)
fig.tight_layout()
plt.show()'''
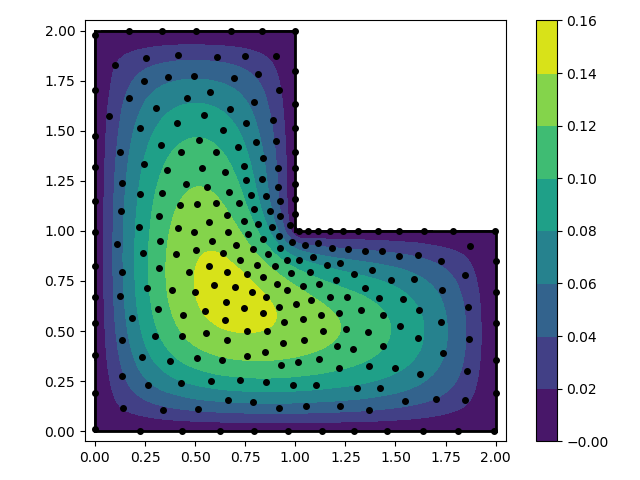
In this example we solve the Poisson equation over an L-shaped
domain with fixed boundary conditions. We use the RBF-FD method. The
RBF-FD method is preferable over the spectral RBF method because it
is scalable and does not require the user to specify a shape
parameter (assuming that we use odd order polyharmonic splines to
generate the weights).
'''
import numpy as np
from scipy.sparse import coo_matrix
from scipy.sparse.linalg import spsolve
import matplotlib.pyplot as plt
from rbf.sputils import add_rows
from rbf.pde.fd import weight_matrix
from rbf.pde.geometry import contains
from rbf.pde.nodes import poisson_disc_nodes
# Define the problem domain with line segments.
vert = np.array([[0.0, 0.0], [2.0, 0.0], [2.0, 1.0],
[1.0, 1.0], [1.0, 2.0], [0.0, 2.0]])
smp = np.array([[0, 1], [1, 2], [2, 3], [3, 4], [4, 5], [5, 0]])
# the node spacing is 0.03 at [1, 1] and increases as we move away
# from that point
def spacing(x):
return 0.04 + 0.08*np.linalg.norm(x - 1.0, axis=1)
n = 25 # stencil size. Increase this will generally improve accuracy
phi = 'phs3' # radial basis function used to compute the weights.
# Odd order polyharmonic splines (e.g., phs3) have
# always performed well for me and they do not require
# the user to tune a shape parameter. Use higher order
# polyharmonic splines for higher order PDEs.
order = 2 # Order of the added polynomials. This should be at least
# as large as the order of the PDE being solved (2 in this
# case). Larger values may improve accuracy
# generate nodes
nodes, groups, _ = poisson_disc_nodes(spacing, (vert, smp))
N = nodes.shape[0]
# create the "left hand side" matrix.
# create the component which evaluates the PDE
A_interior = weight_matrix(nodes[groups['interior']], nodes, n,
diffs=[[2, 0], [0, 2]],
phi=phi, order=order)
# create the component for the fixed boundary conditions
A_boundary = weight_matrix(nodes[groups['boundary:all']], nodes, 1,
diffs=[0, 0])
# Add the components to the corresponding rows of `A`
A = coo_matrix((N, N))
A = add_rows(A, A_interior, groups['interior'])
A = add_rows(A, A_boundary, groups['boundary:all'])
# create "right hand side" vector
d = np.zeros((N,))
d[groups['interior']] = -1.0
d[groups['boundary:all']] = 0.0
# find the solution at the nodes
u_soln = spsolve(A, d)
# Create a grid for interpolating the solution
xg, yg = np.meshgrid(np.linspace(0.0, 2.02, 100),
np.linspace(0.0, 2.02, 100))
points = np.array([xg.flatten(), yg.flatten()]).T
# We can use any method of scattered interpolation (e.g.,
# scipy.interpolate.LinearNDInterpolator). Here we repurpose the
# RBF-FD method to do the interpolation with a high order of
# accuracy
u_itp = weight_matrix(points, nodes, n, diffs=[0, 0]).dot(u_soln)
# mask points outside of the domain
u_itp[~contains(points, vert, smp)] = np.nan
ug = u_itp.reshape((100, 100)) # fold back into a grid
# make a contour plot of the solution
fig, ax = plt.subplots()
p = ax.contourf(xg, yg, ug, np.linspace(-1e-6, 0.16, 9), cmap='viridis')
ax.plot(nodes[:, 0], nodes[:, 1], 'ko', markersize=4)
for s in smp:
ax.plot(vert[s, 0], vert[s, 1], 'k-', lw=2)
ax.set_aspect('equal')
ax.set_xlim(-0.05, 2.05)
ax.set_ylim(-0.05, 2.05)
fig.colorbar(p, ax=ax)
fig.tight_layout()
plt.show()