/Datasets-formalgeo7k-Annotation

formalgeo7k Annotation.

Primary LanguagePythonMIT LicenseMIT

Datasets

Version License Survey

先前的形式化标注工作耗费了大量的人力物力，最终得到了6981道可以成功求解的题目。对于新的几何问题，仍需熟悉FormalGeo形式化系统的专家手动标注， 不能实现完全智能的几何问题自动求解，因此需要开展自动形式化的研究。然而上次标注并未一步到位，formalgeo7k数据集的原始问题来自Geometry3K、GeoQA 和GeoQA+数据集，自然语言问题描述和图像质量低、风格不统一，严重削弱了数据集的价值。关于自动形式化的研究已经在先进模型上进行了初步实验， formalgeo7k原始文本和图像质量较低，严重限制了模型的学习效果；后续的局部关联模型方法也需要更细粒度的图像注释，故当前急切的任务是提高 formalgeo7k自然语言问题描述和图像的质量，统一表述风格。

自然语言问题描述已经使用一些正则化的方法，从形式化语言逆向生成。然而对于几何问题的图像，涉及到跨模态的问题，尚无自动化的方法可以自动生成，只能再 一次辛苦大家标注一下几何图像了。

访问FormalGeo主页获取更多有关FormalGeo的信息。

环境配置

项目和环境配置

下载项目:

$ git clone --depth 1 https://github.com/RuRuo0/Datasets.git

新建Python环境:

$ conda create -n formalgeo python=3.10
$ conda activate formalgeo
$ pip install formalgeo

新建个人分支并推送到远程仓库：

$ git checkout -b your_name
$ git push --set-upstream origin your_name

标注工具

为了实现上述目标，且尽量简化标注工作，最终考虑使用GeoGebra进行图像标注。GeoGebra是一款集数学、几何、代数和微积分于一体的动态数学软件，其中的 几何画图拥有丰富的工具来创建几何图形，并且可通过代数表达式来表示图形。我们可以获取图像 .png 文件和图像 .ggb 文件，并通过解析.ggb文件获取想要的细粒度信息(如点坐标、基元类别等)。
可以直接使用在线网站，也可以将软件下载到本地。

标注协作

本次标注仍然使用Github来协作。在每次标注前，跟主分支同步：

$ git pull origin main

完成每周的标注任务后，提交到远程仓库。在每次提交前，也要跟主分支同步一下。

$ git pull origin main
$ git add projects/formalgeo7k/problems
$ git add projects/formalgeo7k/diagrams
$ git commit -m "your_name week_number"
$ git push

注意：不要add其他文件，否则会导致分支合并冲突。

标注任务和流程

本次标注工作为图像标注，相较于上次形式化标注工作较为轻松，主要有两个任务。第一个任务是检查构图语句是否标注正确，第二个任务是重新画几何图形。标注 过程中主要涉及的对象有：原始几何图像、几何问题JSON文件中的construction_cdl和image_cdl、GeoGebra画图工具。
几何图像文件位于：projects/formalgeo7k/diagrams
几何问题JSON文件位于：projects/formalgeo7k/problems
运行解题程序的脚本位于：projects/formalgeo7k/files/main.py

Task1：构图语句检查

对照原始图像和construction_cdl，查看construction_cdl的标注是否正确，是否有漏掉的图形，是否符合构图语句的标注要求。因为所有问题都已经经过 验证，可以成功求解。当construction_cdl与原始图像不一致时，以construction_cdl为准。这个任务其实是交叉检验一下上次标注的质量。
构图语句的标注方式，具体可见章节构图语句。

Task2：画几何图形

根据几何问题JSON文件、参考原始几何图像、使用GeoGebra重新画几何图像。步骤为：
1.根据JSON文件中的construction_cdl画出基本图形 。可参考原始问题图像，但注意存在新增辅助线和表示点字母不一致等情况。
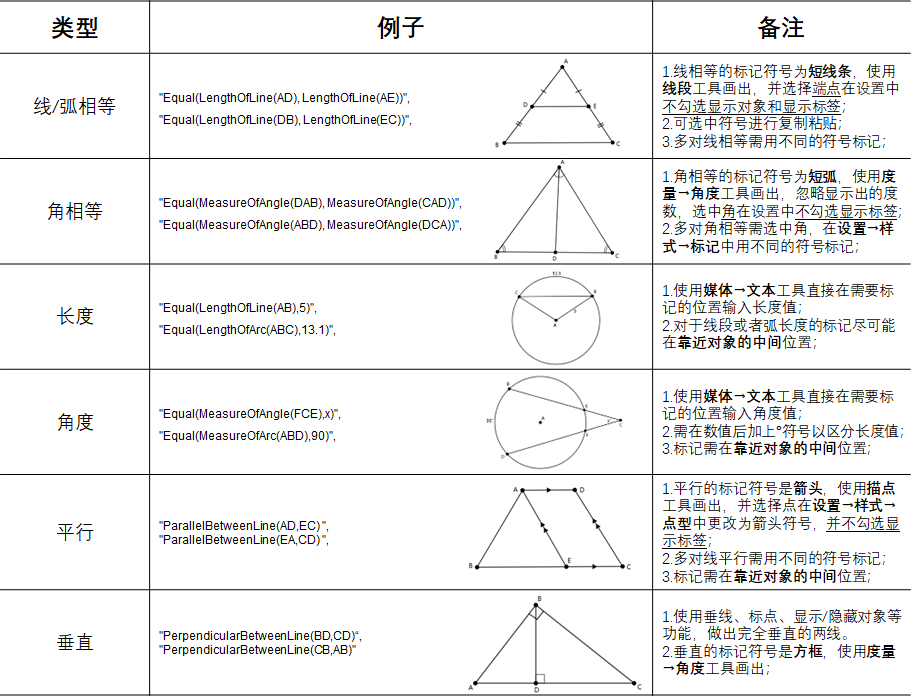
2.图像中能表示的几何关系种类有限，如下图所示。在画图之前，需要检查text_cdl与image_cdl的可标注类型语句：①删去image_cdl中，不在下图可标注 类型中的语句。②若可标注类型语句在text_cdl但不在image_cdl，将其从text_cdl复制到image_cdl。

readme_pic

3.根据JSON文件中的image_cdl在基本图像上标出对应符号和文本，标注方法如上图所示。
4.画完图后，获取图像 .png 文件以及 .ggb 文件，以题号命名，一同上传至projects/formalgeo7k/diagrams文件夹下，并将 原始几何图像文件覆盖。
GeoGebra的画图注意事项，具体可见章节GeoGebra画图。

标注参考：GeoGebra画图

GeoGebra可供操作的工具非常丰富，但我们的标注工作需要使用的工具可以简略到只使用描点、线段、圆、角度、文本这些工具以及设置中对对象的一些编辑。 大家可以自行熟悉GeoGebra的操作，可灵活使用各种方法来画出图像。

使用前设置

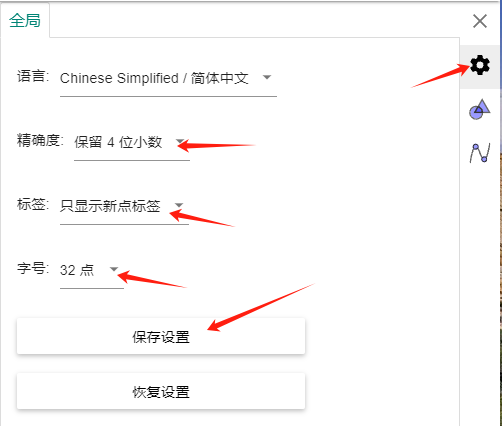
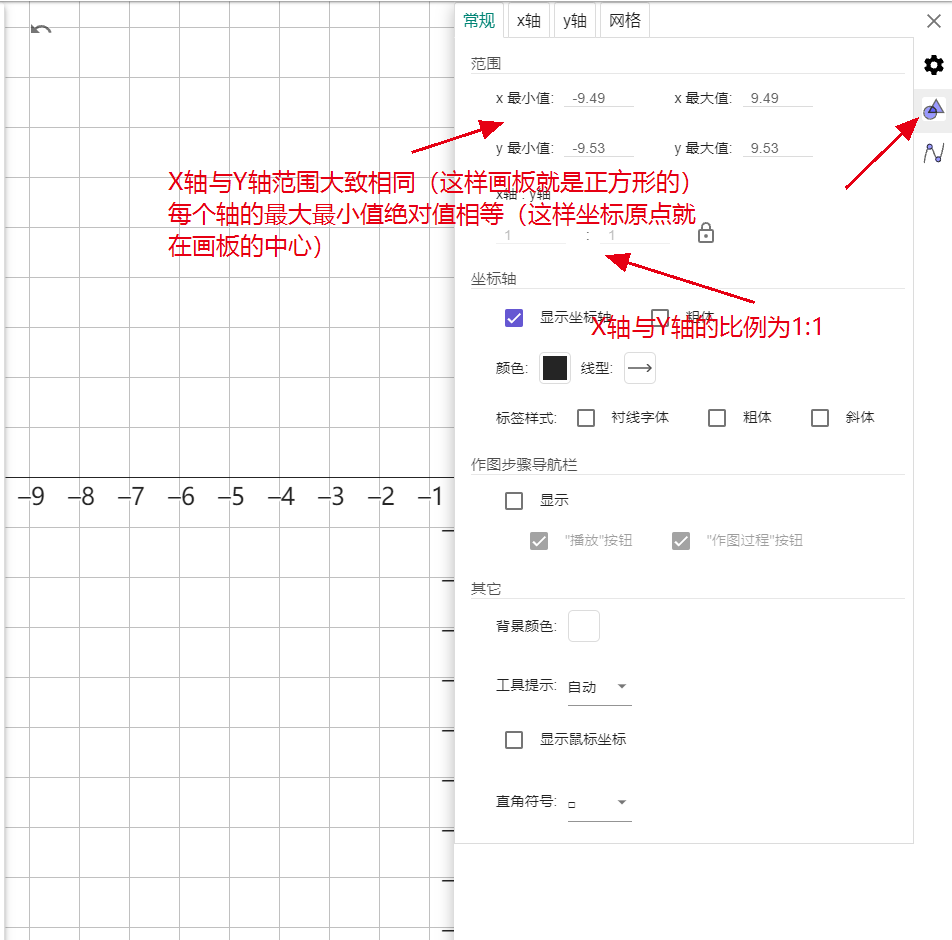
点击右上角设置按钮->设置，打开设置，做以下设置：

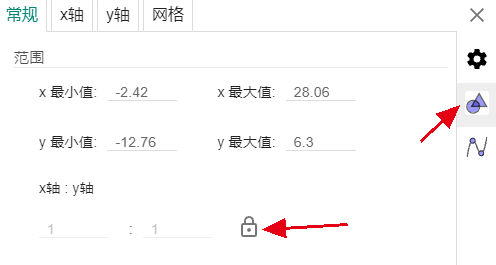
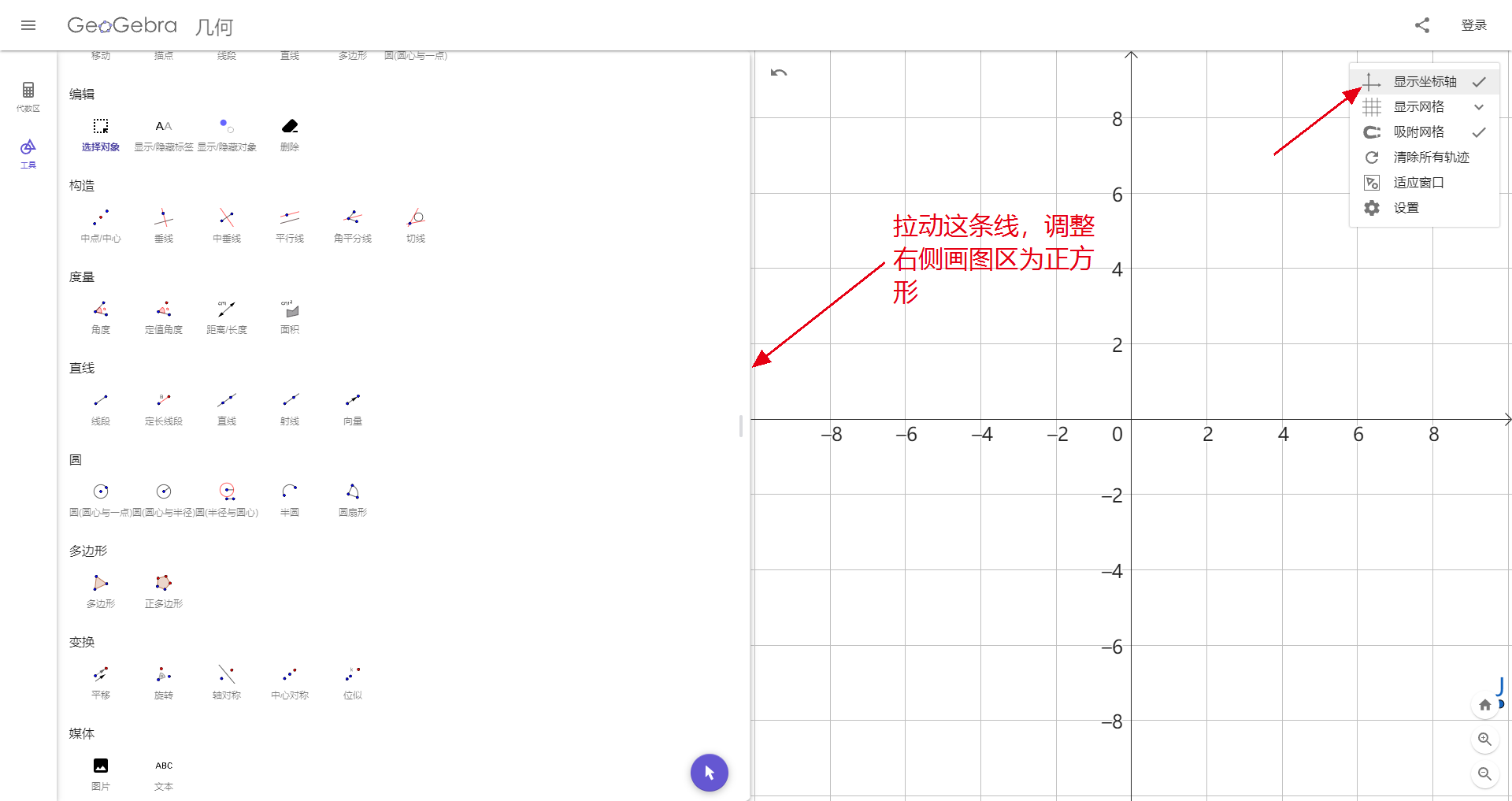
readme_pic
readme_pic
（注：若显示屏分辨率较大，可将字号设置为48点，尽量使字母和符号清晰明显）

拉动中间的线，将右侧画图区调整为正方形。可以在设置中打开坐标轴作为参考，来调整为正方形。 可以点击右下角小房子（标准视图）让坐标轴原点居于画板中心，调整到x和y的范围大致相等即可。

readme_pic

一个调整好的画板如下图所示。画板调整好之后，不要进行放缩和移动。

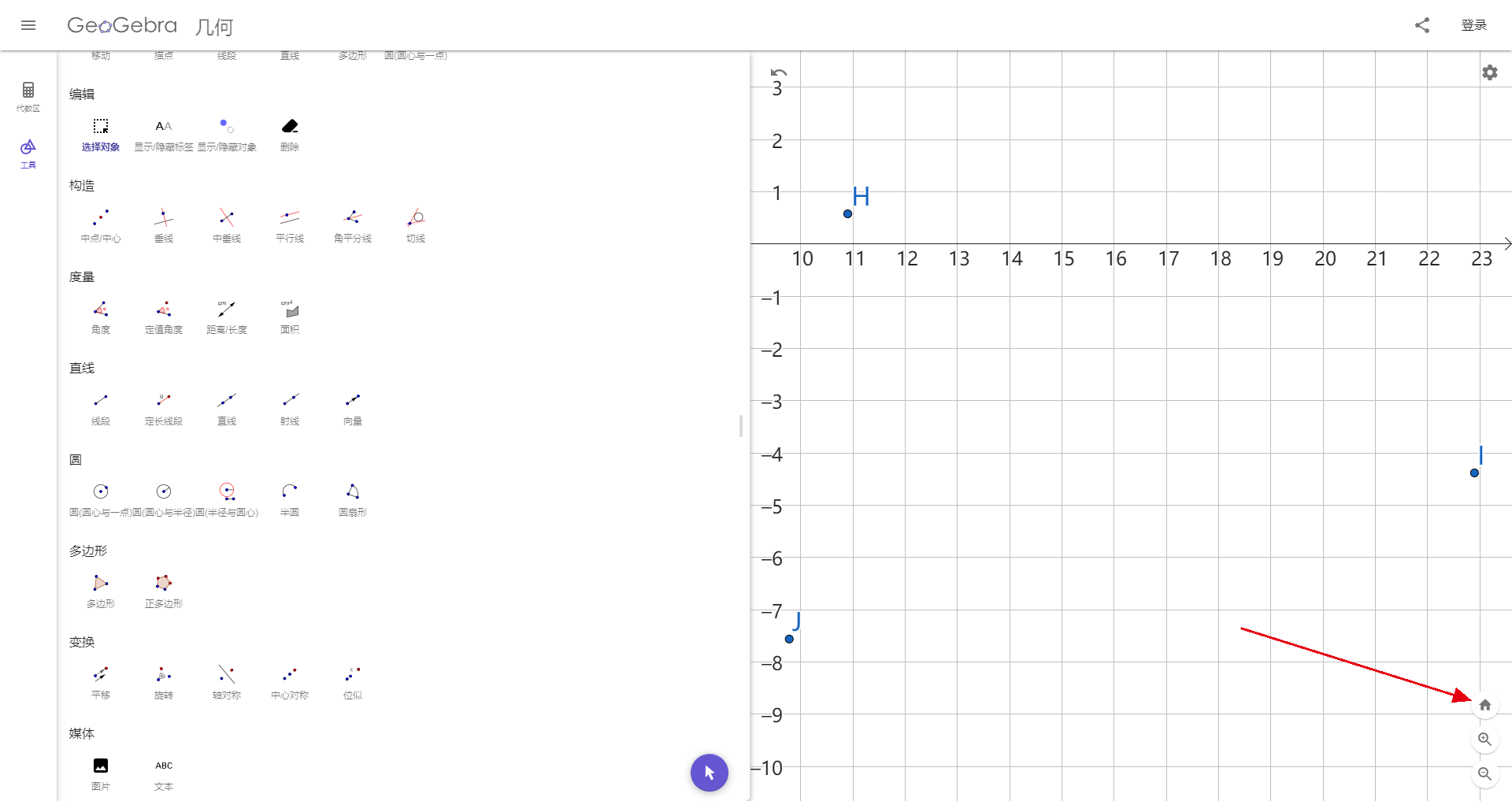
readme_pic

在每次画新的图形前、导出图形前，点击右下角的小房子，转化为标准视图。（如果当前是标准视图，小房子会消失）

readme_pic

导出

我们需要导出几何图形的 .ggb 文件和 .png 文件，需注意：
1.请确认画板已经正确设置为正方形，并处于标准视图。 2.不要导出网格线和坐标轴。在画图时可以点开网格线作为参考，导出png时请关闭网格线和坐标轴。
3.框选所有图形，将所有对象颜色统一成黑色（框选所有对象，右键->设置->颜色）。
4.请确保整个几何图形已大致占据整个画板。
5.右上角导出 .png 文件以及 .ggb 文件，以题号命名，一同上传至projects/formalgeo7k/diagrams文件夹。 （注意不要使用ctrl+s快捷键，可能会覆盖之前已经画好的图形）

注意事项

1.几何图像需要跟JSON文件一一对应。图像中显示的点、线、弧对象一定是和construction_cdl一一对应的，可通过修改点的命名以及选择不显示对象或标签 来实现正确图形显示，后续需从.ggb文件中解析出这些信息。image_cdl只要能在图像上显示出来即可，不涉及.ggb文件的解析。
2.画图时，几何形状应尽量占居整个画板。
3.若修改了JSON文件，请运行projects/formalgeo7k/files/main.py确保问题能成功求解。
4.图形中的符号和文字，应保证尽量不与图形重叠。
5.在画平行与垂直等关系时，应使用GeoGebra的方法画出，标出有用的点，然后将对象隐藏，再用线段将各点连接起来构成图形。这样使用GeoGebra的角度 度量时，一定是直角。

标注参考：构图语句

构图谓词一共有三个，分别是Shape、Collinear和Cocircular。

Shape(*)

Shape是最基本的构图谓词，它使用若干个边或弧来声明一个封闭几何图形，这个几何图形可以是一个角，也可以是边和弧围成的图形。对于封闭几何图形，按照 逆时针方向依次列出图形的边；对于不封闭的几何图形，先连接图形缺口使其转化为封闭的几何图形。

Shape

1.声明一个点
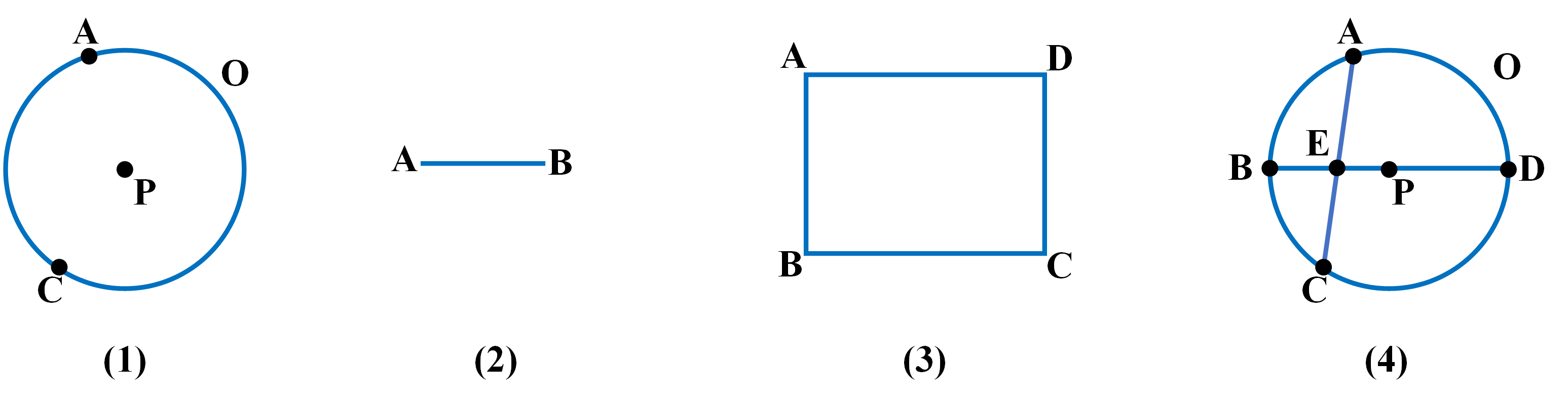
如图1所示，P是圆O的圆心，我们可以这样声明一个点：

Shape(P)

2.声明一条线段
如图2所示，AB是线段的两点，我们可以这样声明线段：

Shape(AB)

当使用Shape声明线段时，默认线段是无向的，所以这样声明也是合法的：

Shape(BA)

3.声明一个角
如图3所示，角B由两条线段构成。需要注意，在声明角时，线段是有向的，两条线出现的顺序按照逆时针的方向，首尾相接。因此角B可以表示为：

Shape(AB,BC)

4.声明一个封闭图形
如果一个边一个边或一个角一个角来声明图形，未免也太麻烦了。我们可以直接声明一个由若干线段和弧构成的图形，在构图阶段，推理器会自动扩展出图形中的 角、线和弧。因此我们在标注图形的构图语句时，先使用Shape声明所有的最小封闭图形，然后在把那些不封闭的最小图形如角、线段、点等声明，就可以声明整个图形。
对于图3中的四边形，我们可以这样声明：

Shape(AB,BC,CD,DA)
Shape(BC,CD,DA,AB)
Shape(CD,DA,AB,BC)
Shape(DA,AB,BC,CD)

一个四边形有上述四种表示，我们选择一种就可以。
更复杂的图形，如图4，可以声明为：

Shape(OAB,BE,EA)
Shape(OBC,CE,EB)
Shape(EC,OCD,DP,PE)
Shape(AE,EP,PD,ODA)

需注意，虽然EP和PD是共线的，但在声明封闭图形时，不能直接声明ED，需要把最小的边都声明出来。
封闭图形可以由线和弧构成，线有两个方向，弧只有一个方向。在声明线时，需要按照逆时针的方向，各点首尾相接；声明弧时，需注意弧只有一种表示方法。
当弧单独出现时，不需要使用Shape来声明，因为弧的出现必然伴随着Cocircular谓词，所有弧将会由Cocircular谓词自动扩展得到。

Collinear(*)

Collinear用来声明3个及3个以上的共线点，2点一定是共线的，所以不用声明2点。

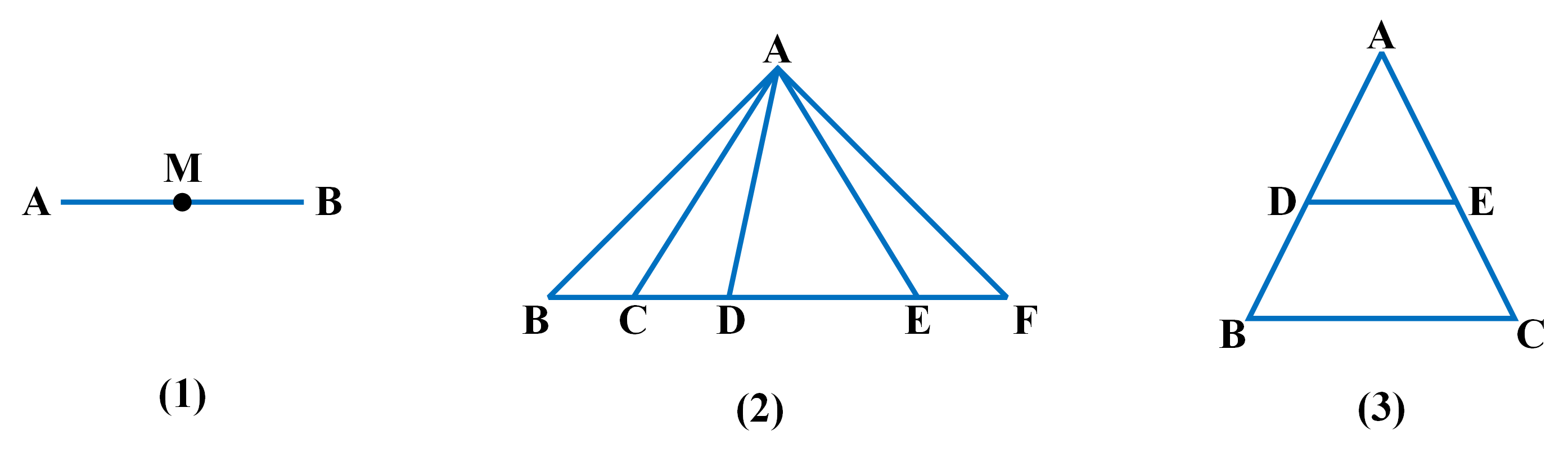
Collinear

共线声明是及其简单的，只要按顺序列出一条线上所有的点即可，如图1中的共线可声明为：

Collinear(AMB)

共线没有方向之分，从另一个方向声明也是合法的：

Collinear(BMA)

图2中的共线可声明为：

Collinear(BCDEF)

图3中的共线可声明为：

Collinear(ADB)
Collinear(AEC)

共线会在推理器中自动扩展出所有的线和平角，如Collinear(AMB)会扩展得到Line(AM),Line(MB),Line(AM),Angle(AMB),Angle(BMA)。

Cocircular(O,*)

Cocircular用来声明共圆的若干个点，与Collinear相同，按照顺序列出若干点即可；但也与Collinear不同，一是即使1个点在圆上也要声明，二是共圆的 声明按照逆时针方向，且从任何点开始都可。

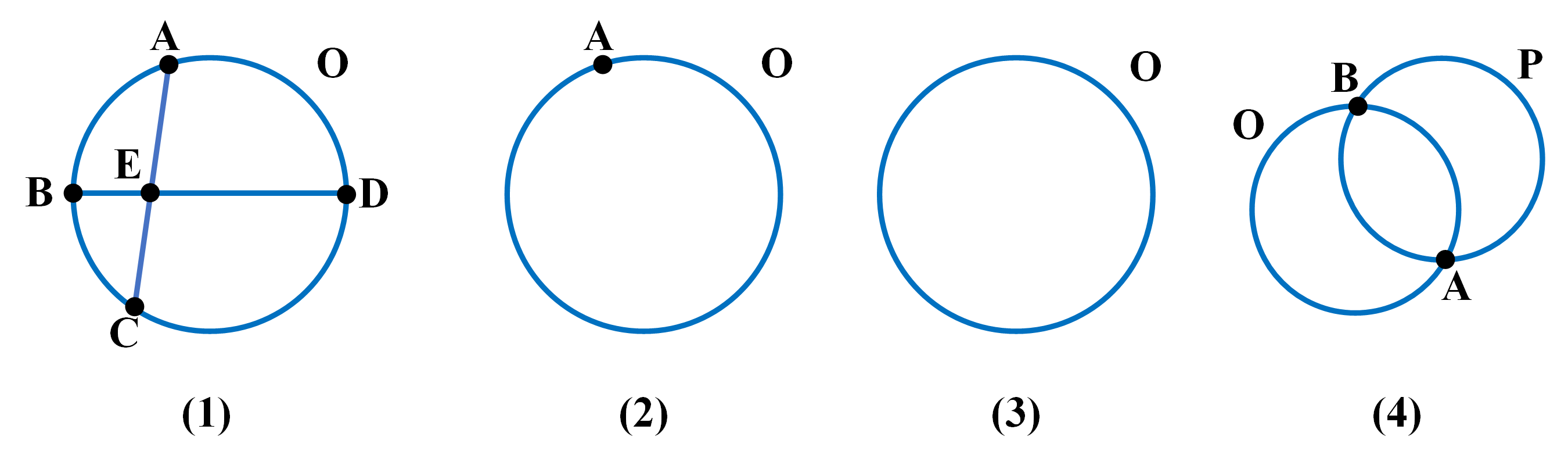
Cocircular

在图1中，共圆的几点可声明为：

Cocircular(O,ABCD)
Cocircular(O,BCDA)
Cocircular(O,CDAB)
Cocircular(O,DABC)

图1的共圆声明可以有上述4种形式，任选其1即可。图2到图4是几种比较特殊的共圆声明。 图2的圆上只有1个点，也要声明：

Cocircular(O,A)

图3圆上没有点，也要声明：

Cocircular(O)

图4两圆有公共点，要分别声明：

Cocircular(O,AB)
Cocircular(P,BA)

共圆声明后，会自动扩展出所有的弧和圆。

任务分配

Week 1 (240101): form 2024-01-01 to 2024-01-14.

Id Annotator WorkLoad PID Submitted Revision
1 朱娜 100 1-100 √ √
2 郭彦钧 70 101-170 √ √
3 贺艺铭 70 171-240 √ √
4 黄琦珂 70 241-310 √ √
5 胡正彧 70 311-380 √ √
6 金啸笑 70 381-450 √ √
7 李阳 70 451-520 √ √
8 毛晨扬 70 521-590 √ √
9 秦城 70 591-660 √ √
10 岳登峰 70 661-730 √ √
11 张效凯 70 731-800 √ √
12 朱方震 70 801-870 √ √
13 朱哲 70 871-940 √ √
14 邹佳 70 941-1010 √ √

Week 2 (240115): form 2024-01-15 to 2024-01-21.

Id Annotator WorkLoad PID Submitted Revision
1 朱娜 100 1011-1110 √ √
2 郭彦钧 70 1111-1180 √ √
3 贺艺铭 70 1181-1250 √ √
4 黄琦珂 70 1251-1320 √ √
5 胡正彧 70 1321-1390 √ √
6 金啸笑 70 1391-1460 √ √
7 李阳 70 1461-1530 √ √
8 毛晨扬 70 1531-1600 √ √
9 秦城 70 1601-1670 √ √
10 岳登峰 70 1671-1740 √ √
11 张效凯 70 1741-1810 √ √
12 朱方震 70 1811-1880 √ √
13 朱哲 70 1881-1950 √ √
14 邹佳 70 1951-2020 √ √

Week 3 (240122): form 2024-01-22 to 2024-01-28.

Id Annotator WorkLoad PID Submitted Revision
1 朱娜 100 2021-2120 √ √
2 郭彦钧 70 2121-2190 √ √
3 贺艺铭 70 2191-2260 √ √
4 黄琦珂 70 2261-2330 √ √
5 胡正彧 70 2331-2400 √ √
6 金啸笑 70 2401-2470 √ √
7 李阳 70 2471-2540 √ √
8 毛晨扬 70 2541-2610 √ √
9 秦城 70 2611-2680 √ √
10 岳登峰 70 2681-2750 √ √
11 张效凯 70 2751-2820 √ √
12 朱方震 70 2821-2890 √ √
13 朱哲 70 2891-2960 √ √
14 邹佳 70 2961-3030 √ √

Week 4 (240129): form 2024-01-29 to 2024-02-04.

Id Annotator WorkLoad PID Submitted Revision
1 朱娜 100 3031-3130 √ √
2 郭彦钧 70 3131-3200 √ √
3 贺艺铭 70 3201-3270 √ √
4 黄琦珂 70 3271-3340 √ √
5 胡正彧 70 3341-3410 √ √
6 金啸笑 70 3411-3480 √ √
7 李阳 70 3481-3550 √ √
8 毛晨扬 70 3551-3620 √ √
9 秦城 70 3621-3690 √ √
10 岳登峰 70 3691-3760 √ √
11 张效凯 70 3761-3830 √ √
12 朱方震 70 3831-3900 √ √
13 朱哲 70 3901-3970 √ √
14 邹佳 70 3971-4040 √ √

Week 5 (240311): form 2024-03-11 to 2024-03-17.

Id Annotator WorkLoad PID Submitted Revision
1 朱娜 70 4041-4110 √ √
2 郭彦钧 70 4111-4180 √ √
3 贺艺铭 70 4181-4250 √ √
4 黄琦珂 70 4251-4320 √ √
5 胡正彧 70 4321-4390 √ √
6 金啸笑 70 4391-4460 √ √
7 李阳 70 4461-4530 √ √
8 毛晨扬 70 4531-4600 √ √
9 秦城 70 4601-4670 √ √
10 岳登峰 70 4671-4740 √ √
11 张效凯 70 4741-4810 √ √
12 张效凯 70 4811-4880 √ √
13 朱哲 70 4881-4950 √ √
14 邹佳 70 4951-5020 √ √

Week 6 (240318): form 2024-03-18 to 2024-03-24.

Id Annotator WorkLoad PID Submitted Revision
1 朱娜 70 5021-5090 √ √
2 郭彦钧 70 5091-5160 √ √
3 贺艺铭 70 5161-5230 √ √
4 黄琦珂 70 5231-5300 √ √
5 胡正彧 70 5301-5370 √ √
6 金啸笑 70 5371-5440 √ √
7 李阳 70 5441-5510 √ √
8 毛晨扬 70 5511-5580 √ √
9 秦城 70 5581-5650 √ √
10 岳登峰 70 5651-5720 √ √
11 张效凯 70 5721-5790 √ √
12 朱娜 70 5791-5860 √ √
13 朱哲 70 5861-5930 √ √
14 邹佳 70 5931-6000 √ √

Week 7 (240325): form 2024-03-25 to 2024-03-31.

Id Annotator WorkLoad PID Submitted Revision
1 朱娜 71 6001-6071 √ √
2 郭彦钧 70 6072-6141 √ √
3 贺艺铭 70 6142-6211 √ √
4 黄琦珂 70 6212-6281 √ √
5 胡正彧 70 6282-6351 √ √
6 金啸笑 70 6352-6421 √ √
7 李阳 70 6422-6491 √ √
8 毛晨扬 70 6492-6561 √ √
9 秦城 70 6562-6631 √ √
10 岳登峰 70 6632-6701 √ √
11 张效凯 70 6702-6771 √ √
12 朱娜 70 6772-6841 √ √
13 朱哲 70 6842-6911 √ √
14 邹佳 70 6912-6981 √ √