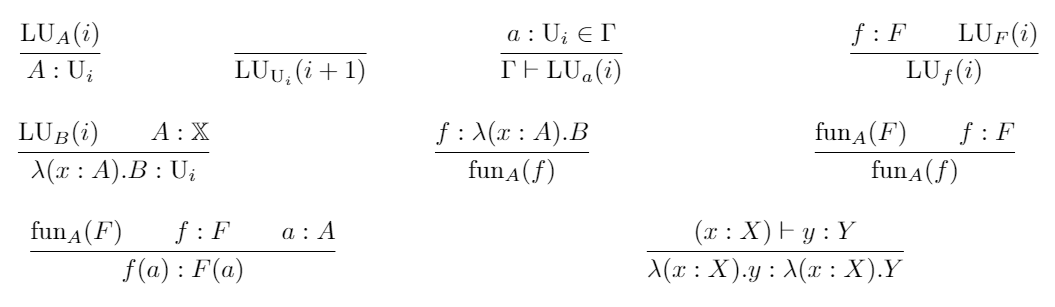Note: This is an older version without variance annotations.
This is a simple prototype implementation of a lambda calculus
in which all types are data (as is typical for dependent types),
and all data are types. This means that we may have terms
true : bool and also terms x : true. This creates an interesting
setting in which all types are their own mini-languages, with synthetic
and functional inhabitants.
All files begin with a module declaration;
module Nat where
After that, a declaration of the form <NAME> : <TYPE> = <TERM>
can be made;
nat : U[0] = (A : U[0]) (s : (a : A) A) (z : A) A
zero : nat = (A : U[0]) (s : (a : A) A) (z : A) z
Note that pi-types and lambda expressions are fused. This means that
(A : U[0]) (s : (a : A) A) (z : A) A could be the natural numbers,
a type, or it could be a function of type (A : U[0]) (s : (a : A) A) (z : A) U[0].
However, there's less freedom in this than one might expect. The following won't
type check;
znat : nat nat = zero nat
since nat is declared to not be a function, and so doesn't accept arguments. One can do the following, though;
natfun : (A : U[0]) (s : (a : A) A) (z : A) U[0]
= (A : U[0]) (s : (a : A) A) (z : A) A
znatfun : natfun = zero
We can encode types with terms that witness other terms. For example;
unit2 : U[0] = (X : U[0]) (x : X) (x' : x) X
tt2 : unit2 = (X : U[0]) (x : X) (x' : x) x
tt' : tt = (X : U[0]) (x : X) (x' : x) x'
For the ordinary unit type;
unit : U[0] = (X : U[0]) (x : X) X
tt : unit2 = (X : U[0]) (x : X) x
tt doesn't have any witnesses, compare with the empty type
empty : U[0] = (X : U[0]) X
Similarly, true and false in the ordinary booleans are also empty. These terms do have identity functions, though
idtt : (tt' : tt) tt = (tt' : tt) tt'
and composition commutativity and identity cancellation of these functions, of course, holds on the nose as they would any lambda expression.
We can define types with synthetic functions, for example;
int : U[0] = (X : U[0]) (x : X) (y : X) (f : (x' : x) y) X
I0 : int = (A : U[0]) (a : A) (b : A) (g : (a' : a) b) a
I1 : int = (X : U[0]) (x : X) (y : X) (f : (x' : x) y) y
If : (i0 : I0) I1
= (i0 : I0) (X : U[0]) (x : X) (y : X) (f : (x' : x) y) f (i0 X x y f)
- Navigate to directory and run
cabal install - The
higerlc.exewill appear in.\dist\build\higerlc\ - Load a program with
higerlc.exe Nat.hlc
None: I don't know of anything similar to this, but I'd be surprised if no one thought to do something like this in the past. If you know of anything, especially as it relates to the consistency of this kind of system, feel free to let me know.
Since the initial release, I've found some documents pertaining to type theories with a single binder. See, for example;
Typed λ-calculi with one binder: http://www.macs.hw.ac.uk/~fairouz/forest/papers/journals-publications/jfp05.pdf
Though, I haven't found anything exactly like the system I have here.
Anthony Hart