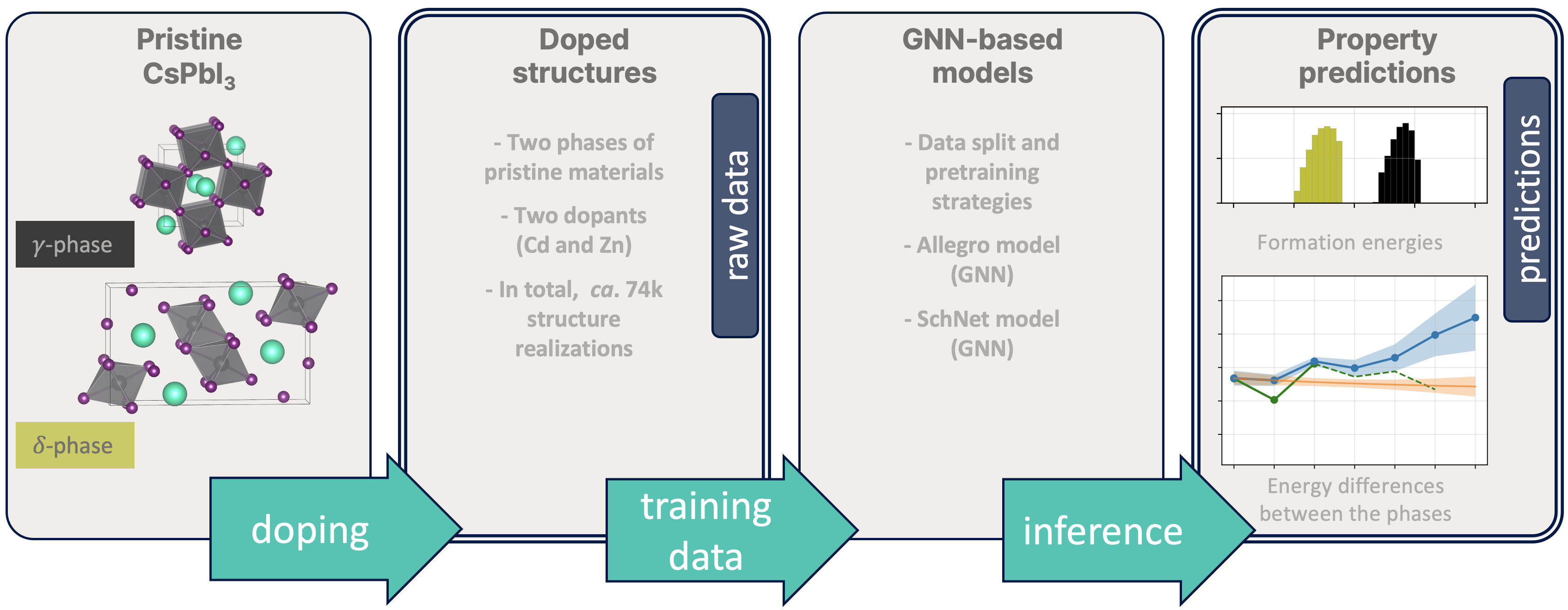
Doping of inorganic lead halide perovskite
More details can be found in the paper.
If you are using this dataset in your research paper, please cite us as
@article{EREMIN2024112672,
title = {Graph neural networks for predicting structural stability of Cd- and Zn-doped γ-CsPbI3},
journal = {Computational Materials Science},
volume = {232},
pages = {112672},
year = {2024},
issn = {0927-0256},
doi = {https://doi.org/10.1016/j.commatsci.2023.112672},
url = {https://www.sciencedirect.com/science/article/pii/S0927025623006663},
author = {Roman A. Eremin and Innokentiy S. Humonen and Alexey A. Kazakov and Vladimir D. Lazarev and Anatoly P. Pushkarev and Semen A. Budennyy}}
The dataset contains Cd- and Zn-doped CsPbI3 systems in two polymorphic modifications and predictions of their formation energies made using various GGNs trained on the DFT derived properties. In our pipeline, we used
- three pretraining modes: no pretraining, pretraining on the whole Open Catalyst Project (OCP) dataset and pretraining on a specially selected slice of the Aflow database;
- two architectures: SchNet and Allegro (for more informations see the Models sections);
- and two model types: both-both and element-both, which means that for the first type the training set contains both Cd-doped systems and Zn-doped systems in both phases, while the for the second one (element-both) the training set contains only Cd-doped systems or Zn-doped (in both phases again). For each combination, listed in the table below, we created 48 train-validation splits with 12 different distribution of defects and trained 48 (96 for element-both) models.
| pretraining mode | both-both | element-both |
|---|---|---|
| non-pretrained | SchNet, Allegro | SchNet, Allegro |
| OCP | Allegro | Allegro |
| Aflow | Allegro | Allegro |
Thus, each presented pandas dataframe contains atomic numbers (i.e. systems itself), metainformation columns, DFT-calculated energies, subsample indicators and 48 (mentioned earlier) GNN predictions. Atomic numbers, metainformation, DFT_energies and subsample indicators are identical in all datasets. More detailed description you can find in the table below.
| ordinal number | column tag | content description |
|---|---|---|
| 1 | phase | yellow/black (corresponds to the phase studied) |
| 2 | supercell | the supercells used (depends on phase) |
| 3 | subst | the number of substituted Pb positions |
| 4 | index | structure id (unique within a certain composition) |
| 5 | weight | corresponds to the number of symmetrically equivalent structures within combinatorial composition/configuration space |
| 6 | dopant | Cd/Zn (dopant type in the structure) |
| 7 | space_group_number | space symmetry of the doped structure before relaxation |
| 8 | formula | chemical formula (OrderedDict type) |
| 9 | natoms | 160 (the number of atoms in the model cells - constant feature) |
| 10 | atomic_numbers | atomic numbers of the structure |
| 11 | nelements | the number of chemical elements in the structure |
| 12 | cell | model cell sizes (before relaxation - constant feature for a certain phase) |
| 13 | pos | atomic positions (before relaxation) |
| 14-61 | val_i | GNN-predicted formation energy per atom (in eV/atom) for the |
| 62 | relaxed_cell_DFT | model cell sizes after DFT relaxation |
| 63 | relaxed_pos_DFT | DFT-relaxed atomic positions |
| 64 | relaxed_pressure_DFT | pressure (in kbar) for the DFT-relaxed structure |
| 65 | relaxed_forces_DFT | atomic forces (in eV/angstrom) for the DFT-relaxed structure |
| 66 | relaxed_energy_DFT | relaxed energy per cell (in eV) for the DFT-relaxed structure |
| 67 | relaxed_energy_pa_DFT | relaxed energy per atom (in eV/atom) for the DFT-relaxed structure |
| 68 | formation_energy_pa_DFT | formation energy per atom (in eV/atom) for the DFT-relaxed structure |
| 69-116 | val_i_DFT | boolean flag showing whether the configuration is in the |
| 117 | inWhichPart | tr_val, test, or inference (corresponds to the data usage within the approach proposed) |
The repository also contains a Jupyter Notebook file with utils and visualisation scripts. You can calculate and visualise energy distributions, RMSEs, predictions, etc.