AIRI-Institute/nablaDFT

nablaDFT: Large-Scale Conformational Energy and Hamiltonian Prediction benchmark and dataset

$\nabla^2$ DFT: A Universal Quantum Chemistry Dataset of Drug-Like Molecules and a Benchmark for Neural Network Potentials

This is the repository for nablaDFT Dataset and Benchmark. The current version is 2.0. The code and data from the initial publication are accessible here: 1.0 branch.
Methods of computational quantum chemistry provide accurate approximations of molecular properties crucial for computer-aided drug discovery and other areas of chemical science. However, high computational complexity limits the scalability of their applications. Neural network potentials (NNPs) are a promising alternative to quantum chemistry methods, but they require large and diverse datasets for training. This work presents a new dataset and benchmark called $\nabla^2$ DFT that is based on the nablaDFT. It contains twice as much molecular structures, three times more conformations, new data types and tasks, and state-of-the-art models. The dataset includes energies, forces, 17 molecular properties, Hamiltonian and overlap matrices, and a wavefunction object. All calculations were performed at the DFT level (ωB97X-D/def2-SVP) for each conformation. Moreover, $\nabla^2$ DFT is the first dataset that contains relaxation trajectories for a substantial number of drug-like molecules. We also introduce a novel benchmark for evaluating NNPs in molecular property prediction, Hamiltonian prediction, and conformational optimization tasks. Finally, we propose an extendable framework for training NNPs and implement 10 models within it.
More details can be found in the version 1 paper and version 2 paper.

If you are using nablaDFT in your research paper, please cite us as

@article{khrabrov2024nabla2dftuniversalquantumchemistry,
      title={$\nabla^2$DFT: A Universal Quantum Chemistry Dataset of Drug-Like Molecules and a Benchmark for Neural Network Potentials}, 
      author={Kuzma Khrabrov and Anton Ber and Artem Tsypin and Konstantin Ushenin and Egor Rumiantsev and Alexander Telepov and Dmitry Protasov and Ilya Shenbin and Anton Alekseev and Mikhail Shirokikh and Sergey Nikolenko and Elena Tutubalina and Artur Kadurin},
      year={2024},
      eprint={2406.14347},
      archivePrefix={arXiv},
      primaryClass={physics.chem-ph},
      url={https://arxiv.org/abs/2406.14347}, 
}

@article{10.1039/D2CP03966D,
author ="Khrabrov, Kuzma and Shenbin, Ilya and Ryabov, Alexander and Tsypin, Artem and Telepov, Alexander and Alekseev, Anton and Grishin, Alexander and Strashnov, Pavel and Zhilyaev, Petr and Nikolenko, Sergey and Kadurin, Artur",
title  ="nablaDFT: Large-Scale Conformational Energy and Hamiltonian Prediction benchmark and dataset",
journal  ="Phys. Chem. Chem. Phys.",
year  ="2022",
volume  ="24",
issue  ="42",
pages  ="25853-25863",
publisher  ="The Royal Society of Chemistry",
doi  ="10.1039/D2CP03966D",
url  ="http://dx.doi.org/10.1039/D2CP03966D"}

Installation

git clone https://github.com/AIRI-Institute/nablaDFT && cd nablaDFT/
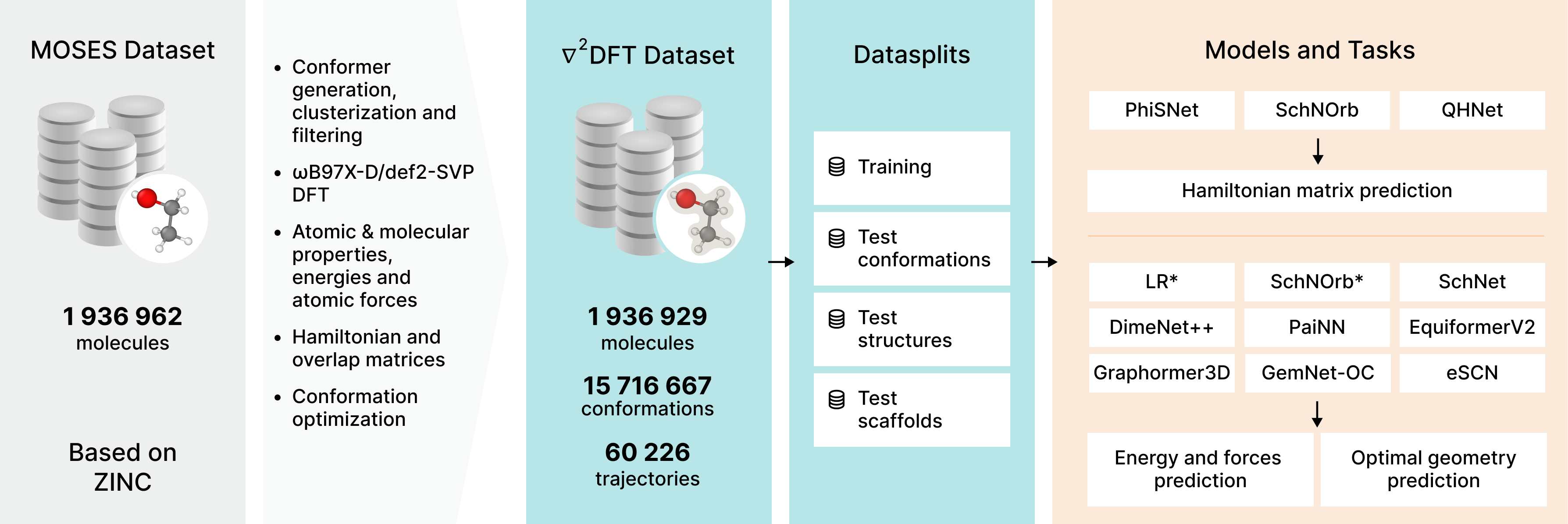
pip install .

Dataset

We propose a benchmarking dataset based on a subset of Molecular Sets (MOSES) dataset. Resulting dataset contains 1 936 931 molecules with atoms C, N, S, O, F, Cl, Br, H. It contains 226 424 unique Bemis-Murcko scaffolds and 34 572 unique BRICS fragments.
For each molecule in the dataset we provide from 1 to 62 unique conformations, with 12 676 264 total conformations. For each conformation, we have calculated its electronic properties including the energy (E), DFT Hamiltonian matrix (H), and DFT overlap matrix (S). All properties were calculated using the Kohn-Sham method at ωB97X-D/def2-SVP levels of theory using the quantum-chemical software package Psi4, version 1.5.
We provide several splits of the dataset that can serve as the basis for comparison across different models.
As part of the benchmark, we provide separate databases for each subset and task and a complete archive with wave function files produced by the Psi4 package that contains quantum chemical properties of the corresponding molecule and can be used in further computations.

Downloading dataset

Hamiltonian databases

Links to hamiltonian databases including different train and test subsets are in file Hamiltonian databases

Energy databases

Links to energy databases including different train and test subsets are in file Energy databases

Raw psi4 wave functions

Links to tarballs: wave functions

Summary file

The csv file with conformations index, SMILES, atomic DFT properties and wfn archive names: summary.csv

The csv file with conformations index, energies and forces for optimization trajectories: trajectories_summary.csv

Conformations files

Tar archive with xyz files archive

Accessing elements of the dataset

Hamiltonian database

Downloading of the smallest file (train-tiny data split, 14 Gb):

wget https://a002dlils-kadurin-nabladft.obs.ru-moscow-1.hc.sbercloud.ru/data/nablaDFTv2/hamiltonian_databases/train_2k.db

Minimal usage example:

from nablaDFT.dataset import HamiltonianDatabase

train = HamiltonianDatabase("train_2k.db")
# atoms numbers, atoms positions, energy, forces, core hamiltonian, overlap matrix, coefficients matrix,
# moses_id, conformation_id
Z, R, E, F, H, S, C, moses_id, conformation_id = train[0]

Energies database

Downloading of the smallest file (train-tiny data split, 51 Mb):

wget https://a002dlils-kadurin-nabladft.obs.ru-moscow-1.hc.sbercloud.ru/data/nablaDFTv2/energy_databases/train_2k_v2_formation_energy_w_forces.db

Minimal usage example:

from ase.db import connect

train = connect("train_2k_v2_formation_energy_w_forces.db")
atoms_data = train.get(1)

Working with raw psi4 wavefunctions

Downloading of the smallest file (6,8 Gb):

https://a002dlils-kadurin-nabladft.obs.ru-moscow-1.hc.sbercloud.ru/data/moses_wfns_big/wfns_moses_conformers_archive_0.tar
tar -xf wfns_moses_conformers_archive_0.tar
cd mnt/sdd/data/moses_wfns_big/

A variety of properties can be loaded directly from the wavefunction files. See main paper for more details. Properties include DFT matrices:

import numpy as np
wfn = np.load('wfn_conf_50000_0.npy', allow_pickle=True).tolist()
orbital_matrix_a = wfn["matrix"]["Ca"]        # alpha orbital coefficients
orbital_matrix_b = wfn["matrix"]["Cb"]        # beta orbital coefficients
density_matrix_a = wfn["matrix"]["Da"]        # alpha electonic density
density_matrix_b = wfn["matrix"]["Db"]        # beta electonic density
aotoso_matrix = wfn["matrix"]["aotoso"]       # atomic orbital to symmetry orbital transformation matrix
core_hamiltonian_matrix = wfn["matrix"]["H"]  # core Hamiltonian matrix
fock_matrix_a = wfn["matrix"]["Fa"]           # DFT alpha Fock matrix
fock_matrix_b = wfn["matrix"]["Fb"]           # DFT betta Fock matrix

and bond orders for covalent and non-covalent interactions and atomic charges:

import psi4
wfn = psi4.core.Wavefunction.from_file('wfn_conf_50000_0.npy')
psi4.oeprop(wfn, "MAYER_INDICES")
psi4.oeprop(wfn, "WIBERG_LOWDIN_INDICES")
psi4.oeprop(wfn, "MULLIKEN_CHARGES")
psi4.oeprop(wfn, "LOWDIN_CHARGES")
meyer_bos = wfn.array_variables()["MAYER INDICES"]  # Mayer bond indices
lodwin_bos = wfn.array_variables()["WIBERG LOWDIN INDICES"]  # Wiberg bond indices
mulliken_charges = wfn.array_variables()["MULLIKEN CHARGES"]  # Mulliken atomic charges
lowdin_charges = wfn.array_variables()["LOWDIN CHARGES"]  # Löwdin atomic charges

Models

• Unifying machine learning and quantum chemistry with a deep neural network for molecular wavefunctions (SchNOrb)
• SE(3)-equivariant prediction of molecular wavefunctions and electronic densities (PhiSNet)
• A continuous-filter convolutional neural network for modeling quantum interactions (SchNet)
• Equivariant message passing for the prediction of tensorial properties and molecular spectra (PaiNN)
• Fast and Uncertainty-Aware Directional Message Passing for Non-Equilibrium Molecules (DimeNet++)
• EquiformerV2: Improved Equivariant Transformer for Scaling to Higher-Degree Representations (EquiformerV2)
• Reducing SO(3) Convolutions to SO(2) for Efficient Equivariant GNNs (eSCN)
• GemNet-OC: Developing Graph Neural Networks for Large and Diverse Molecular Simulation Datasets (GemNet-OC)
• Benchmarking Graphormer on Large-Scale Molecular Modeling Datasets (Graphormer3D)
• Efficient and Equivariant Graph Networks for Predicting Quantum Hamiltonian (QHNet)

Run

For task start run this command from repository root directory:

python run.py --config-name <config-name>.yaml

For the detailed run configuration please refer to run configuration README.

Datamodules

To create a dataset, we use interfaces from ASE, PyTorch Geometric and PyTorch Lightning. An example of the initialisation of ASE-type data classes (for SchNet, PaiNN models) is presented below:

datamodule = ASENablaDFT(split="train", dataset_name="dataset_train_tiny")
datamodule.prepare_data()
# access to dataset
datamodule.dataset

For PyTorch Geometric data dataset initialized with PyGNablaDFTDatamodule:

datamodule = PyGNablaDFTDataModule(root="path-to-dataset-dir", dataset_name="dataset_train_tiny", train_size=0.9, val_size=0.1)
datamodule.setup(stage="fit")

Similarly, Hamiltonian-type data classes (for SchNOrb, PhiSNet models) are initialised in the following way:

datamodule = PyGHamiltonianDataModule(root="path-to-dataset-dir", dataset_name="dataset_train_tiny", train_size=0.9, val_size=0.1)
datamodule.setup(stage="fit")

Dataset itself could be acquired in the following ways:

datamodule.dataset_train
datamodule.dataset_val

List of available dataset splits could be obtained with:

from nablaDFT.dataset import dataset_registry
dataset_registry.list_datasets("energy")  # for energy databases
dataset_registry.list_datasets("hamiltonian")  # for hamiltonian databases

For more detailed list of datamodules parameters please refer to datamodule example config.

Checkpoint

Available model checkpoints could be obtained with:

from nablaDFT import model_registry
model_registry.list_models()

For complete list of available checkpoints for different training splits see Pretrained models.
Links for checkpoints are available here: checkpoints links

Tutorials and examples

• Basic access tutorial
• Meta-information tutorial

Models training and testing example:

• PAINN
• Collab
• GemNet-OC

Models inference example:

• GemNet-OC

Metrics

In the tables below ST, SF, CF denote structures test set, scaffolds test set and conformations test set correspondingly.

Model	MAE for energy prediction $\times 10^{−2} E_h$ (↓)
	Test ST				Test SF				Test CF
	tiny	small	medium	large	tiny	small	medium	large	tiny	small	medium	large
LR	4.86	4.64	4.56	4.56	4.37	4.18	4.12	4.15	3.76	3.61	3.69	3.95
SchNet	1.17	0.90	1.10	0.31	1.19	0.92	1.11	0.31	0.56	0.63	0.88	0.28
SchNOrb	0.83	0.47	0.39	0.39	0.86	0.46	0.37	0.39	0.37	0.26	0.27	0.36
DimeNet++	42.84	0.56	0.21	0.09	37.41	0.41	0.19	0.08	0.42	0.10	0.09	0.07
PAINN	0.82	0.60	0.36	0.09	0.86	0.61	0.36	0.09	0.43	0.49	0.28	0.08
Graphormer3D-small	1.54	0.96	0.77	0.37	1.58	0.94	0.75	0.36	0.99	0.67	0.58	0.39
GemNet-OC	2.79	0.65	0.28	0.22	2.59	0.59	0.27	0.23	0.52	0.20	0.15	0.24
Equiformer_V2	2.81	1.13	0.28	0.19	2.65	1.13	0.28	0.18	0.45	0.23	0.24	0.16
eSCN	1.87	0.47	0.94	0.42	1.87	0.47	0.92	0.42	0.48	0.31	0.80	0.44

Model	MAE for forces prediction $\times 10^{−2} E_h*A^{-1}$ (↓)
	Test ST				Test SF				Test CF
	tiny	small	medium	large	tiny	small	medium	large	tiny	small	medium	large
SchNet	0.44	0.37	0.41	0.16	0.45	0.37	0.41	0.16	0.32	0.30	0.37	0.14
DimeNet++	1.31	0.20	0.13	0.065	1.36	0.19	0.13	0.066	0.26	0.12	0.10	0.062
PAINN	0.37	0.26	0.17	0.058	0.38	0.26	0.17	0.058	0.23	0.22	0.14	0.052
Graphormer3D-small	1.11	0.67	0.54	0.26	1.13	0.68	0.55	0.26	0.82	0.54	0.45	0.23
GemNet-OC	0.14	0.051	0.036	0.021	0.10	0.051	0.036	0.021	0.073	0.042	0.032	0.021
Equiformer_V2	0.30	0.23	0.21	0.17	0.31	0.23	0.21	0.17	0.16	0.15	0.16	0.13
eSCN	0.10	0.051	0.036	0.021	0.10	0.051	0.036	0.021	0.065	0.037	0.029	0.021

Model	MAE for Hamiltonian matrix prediction $\times 10^{−4} E_h$ (↓)
	Test ST				Test SF				Test CF
	tiny	small	medium	large	tiny	small	medium	large	tiny	small	medium	large
SchNOrb	198	196	196	198	199	198	200	199	215	207	207	206
PhiSNet	1.9	3.2(*)	3.4(*)	3.6(*)	1.9	3.2(*)	3.4(*)	3.6(*)	1.8	3.3(*)	3.5(*)	3.7(*)
QHNet	9.8	7.9	5.2	6.9(*)	9.8	7.9	5.2	6.9(*)	8.4	7.3	5.2	6.8(*)

Model	MAE for overlap matrix prediction $\times 10^{−5}$(↓)
	Test ST				Test SF				Test CF
	tiny	small	medium	large	tiny	small	medium	large	tiny	small	medium	large
SchNOrb	1320	1310	1320	1340	1330	1320	1330	1340	1410	1360	1370	1370
PhiSNet	2.7	3.0(*)	2.9(*)	3.3(*)	2.6	2.9(*)	2.9(*)	3.2(*)	3.0	3.2(*)	3.1(*)	3.5(*)

We test the ability of the trained models to find low energy conformations.

Model	Optimization metrics
	Optimization $pct$ % (↑)				Optimization $pct_{div}$ % (↓)				Optimization success $pct$ % (↑)
	tiny	small	medium	large	tiny	small	medium	large	tiny	small	medium	large
SchNet	39.07	40.95	36.60	80.25	42.4	38.25	47.65	6.05	0	0	0	3.50
PAINN	60.60	67.30	74.67	98.45	18.70	14.55	14.00	1.50	0	0.12	2.33	77.36
DimeNet++	33.80	89.30	93.22	96.29	96.40	20.70	8.25	1.70	0	12.55	33.52	55.14

Fields with - or * symbols correspond to the models, which haven't converged and will be updated in the future.