This repository contains codes of the method Joint Probability Distribution Adaptation. This paper proposed a simple but efficient discriminative joint probability metric for domain adaptation. We verified its performance by embedding it to a joint probability domain adaptation (JPDA) framework. Compared with traditional MMD approaches, JPDA has a simpler form, and is more effective in measuring the discrepancy between different domains. Experiments on six image classification datasets verified the effectiveness of JPDA.
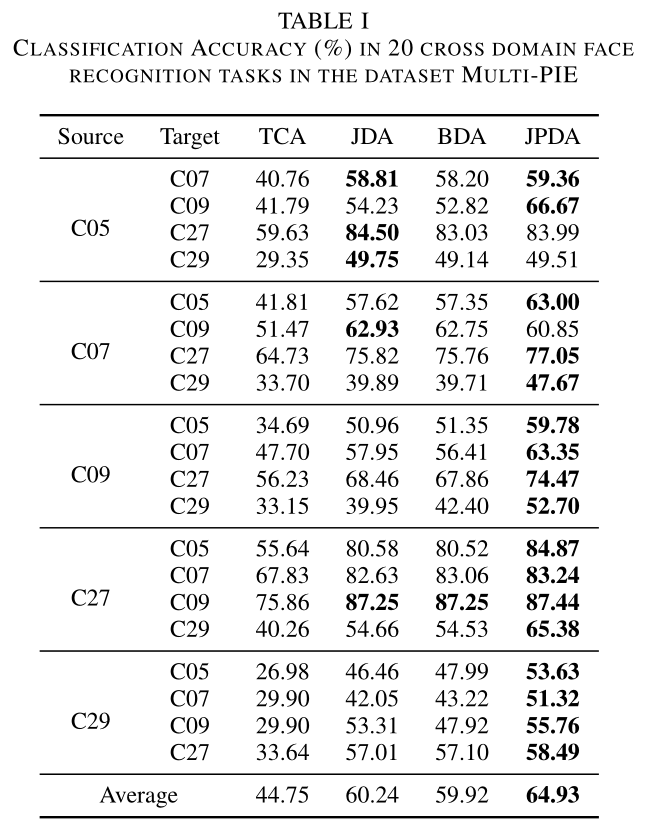
The average accuracies on the Multi-PIE dataset are shown in Table 1. JPDA outperforms all the joint MMD based approaches in most tasks, and achieve an accuracy improvement of 4.69% compared with JDA.
The code is MATLAB code works in Windows 10 system.
Code files introduction:
demo_classify_office.m -- demo file, JPDA on 12 cross-domain image classification tasks on dataset Office+Caltech.
demo_classify_other.m -- demo file, joint probability distribution adaptation (JPDA) over 4 cross-domain image classification tasks on datasets COIL, USPS and MNIST.
demo_classify_pie.m -- demo file, JPDA on 20 cross-domain image classification tasks on dataset Multi-PIE.
JPDA.m -- function file, it's the implementation of JPDA approach. Please find the specific input/output instructions in the function comments.
This code is corresponding to our IJCNN 2020 paper below:
@inproceedings{wenz20djpmmd,
title={Discriminative Joint Probability Maximum Mean Discrepancy (DJP-MMD) for Domain Adaptation},
author={Zhang, Wen and Wu, Dongrui},
booktitle={Int'l Joint Conf. on Neural Networks, IJCNN},
year={2020},
month=jul,
address={Glasgow, UK},
note={Accepted},
}
Please cite our paper if you like or use our work for your research, thank you very much!
In the toy experiments in our paper, we only verified the effectiveness of DJP-MMD by embedding it to the JDA framework (a regularization term and a principal component preservation constraint) for simplicity, and the results were indeed significantly better than the joint or balanced MMD.
In our later experiments (use DJP-MMD in TJM or JGSA etc.), we found that a more robust metric to measure the discrepancy may be the marginal MMD with DJP-MMD, or GFK preprocessed data with DJP-MMD.