| Documentation | Build Status | Downloads |
|---|---|---|
  |
This Julia package aims at performing automatic bifurcation analysis of possibly large dimensional equations F(u, λ)=0 where λ∈ℝ by taking advantage of iterative methods, dense / sparse formulation and specific hardwares (e.g. GPU).
It incorporates continuation algorithms (PALC, deflated continuation, ...) based on a Newton-Krylov method to correct the predictor step and a Matrix-Free/Dense/Sparse eigensolver is used to compute stability and bifurcation points.
The idea is to be able to seemingly switch the continuation algorithm a bit like changing the time stepper (Euler, RK4,...) for ODEs.
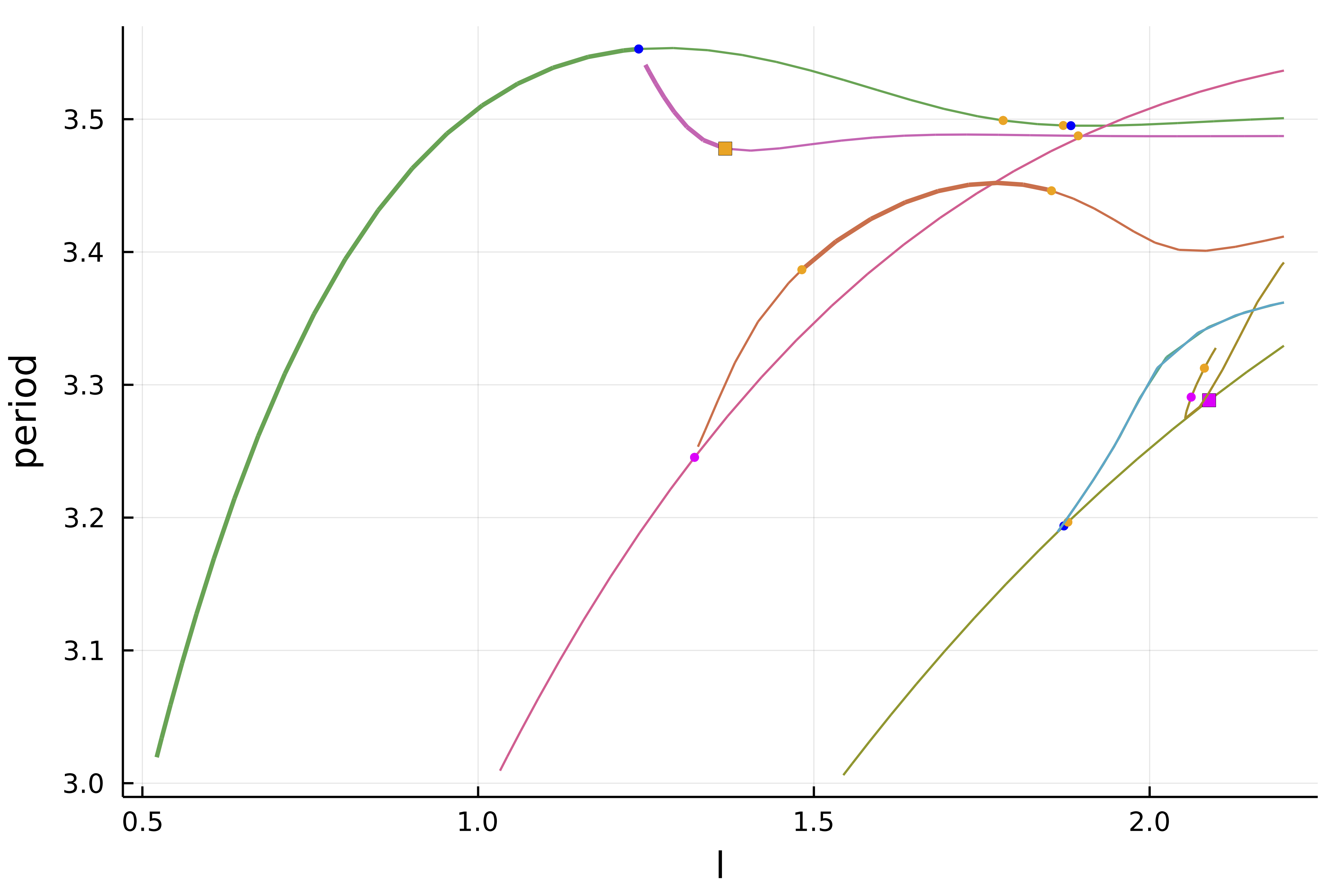
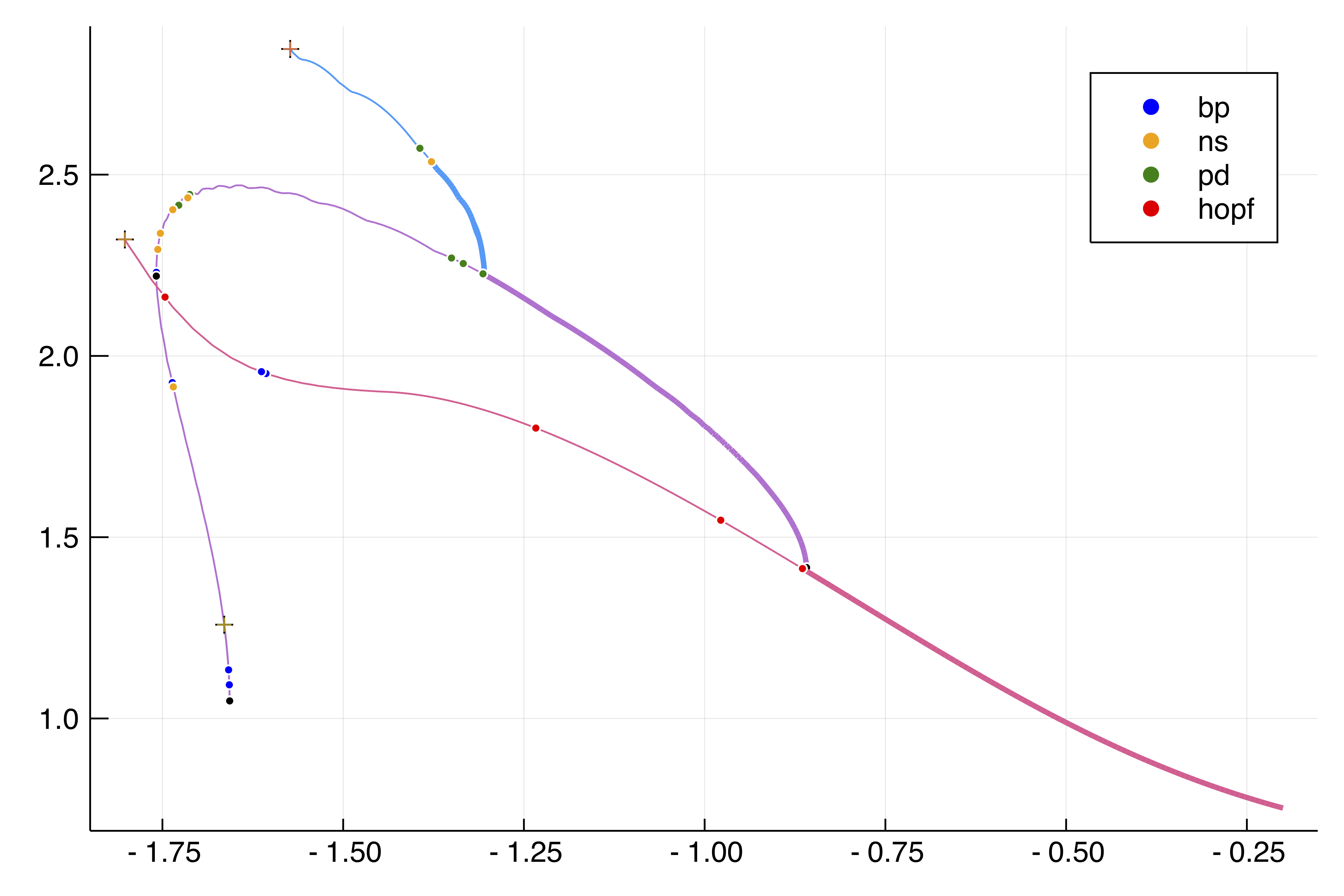
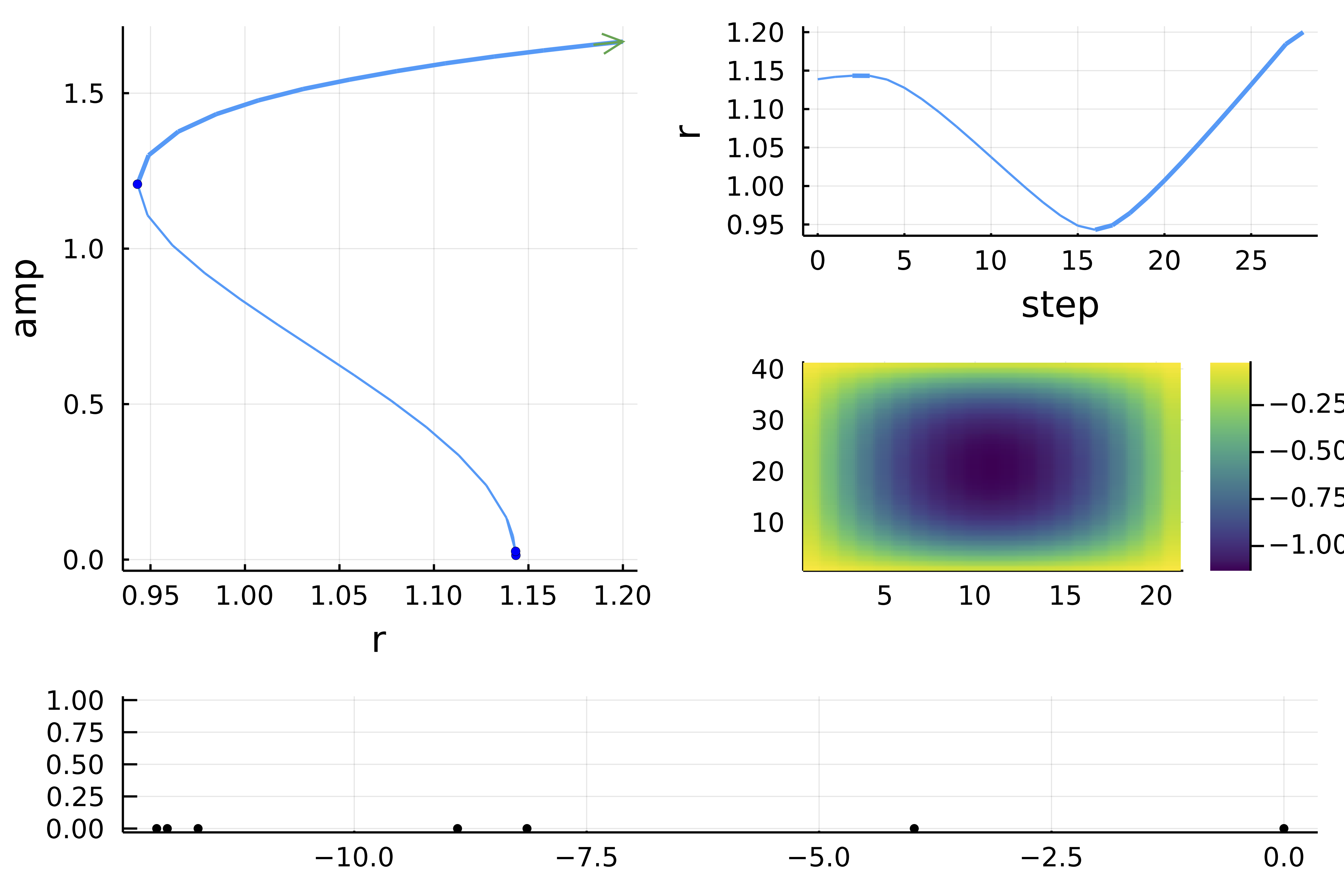
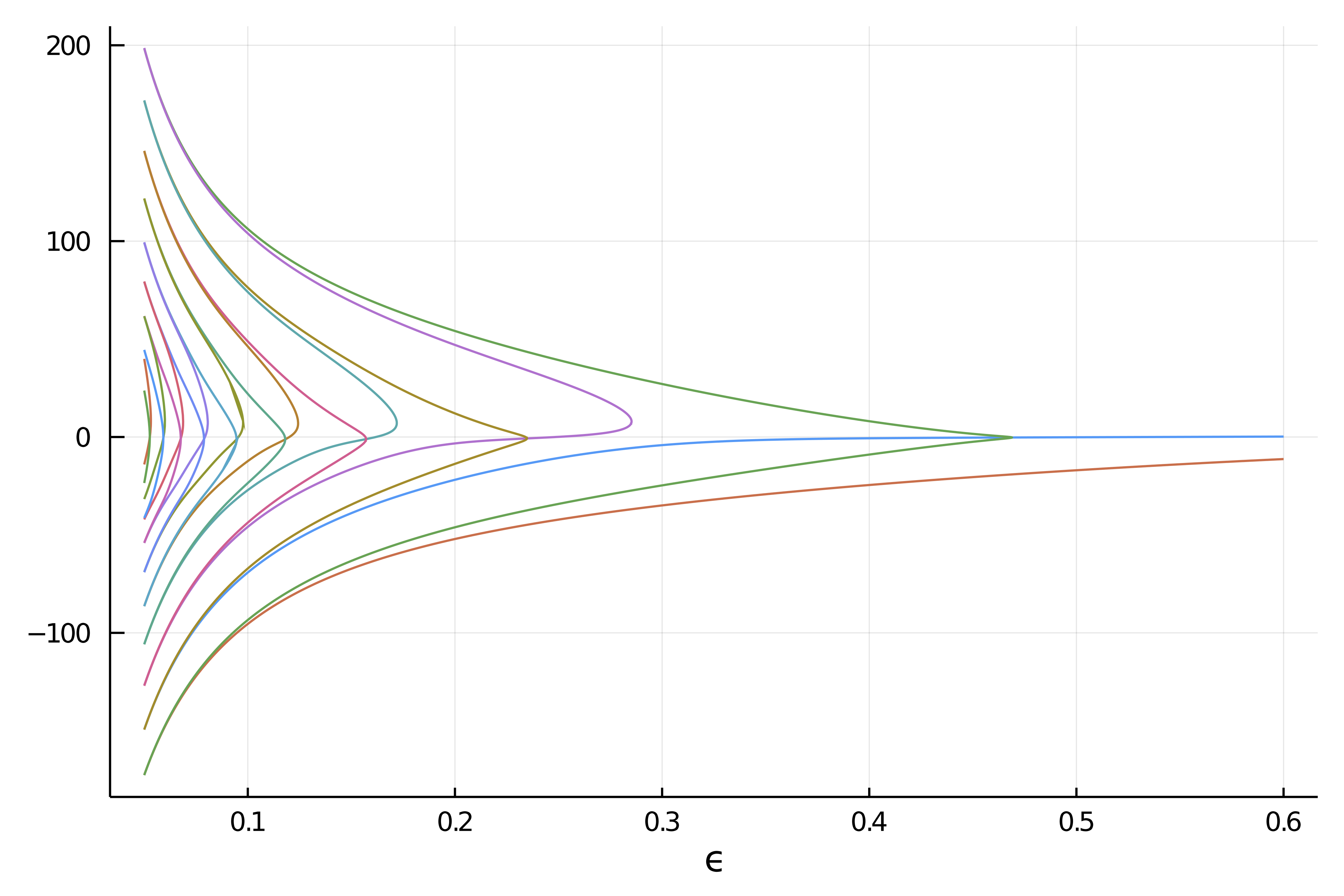
BifurcationKit can also seek for periodic orbits of Cauchy problems. It is by now, one of the only softwares which provides shooting methods AND methods based on finite differences or collocation to compute periodic orbits.
The current focus is on large scale nonlinear problems and multiple hardwares. Hence, the goal is to use Matrix Free methods on GPU (see PDE example and Periodic orbit example) or on a cluster to solve non linear PDE, nonlocal problems, compute sub-manifolds...
Despite this focus, the package can easily handle low dimensional problems and specific optimizations are regularly added.
If you use BifurcationKit.jl in your work, we ask that you cite the following paper. Open source development as part of academic research strongly depends on this. Please also consider starring this repository if you like our work, this will help us to secure funding in the future. It is referenced on HAL-Inria as follows:
@misc{veltz:hal-02902346,
TITLE = {{BifurcationKit.jl}},
AUTHOR = {Veltz, Romain},
URL = {https://hal.archives-ouvertes.fr/hal-02902346},
INSTITUTION = {{Inria Sophia-Antipolis}},
YEAR = {2020},
MONTH = Jul,
KEYWORDS = {pseudo-arclength-continuation ; periodic-orbits ; floquet ; gpu ; bifurcation-diagram ; deflation ; newton-krylov},
PDF = {https://hal.archives-ouvertes.fr/hal-02902346/file/354c9fb0d148262405609eed2cb7927818706f1f.tar.gz},
HAL_ID = {hal-02902346},
HAL_VERSION = {v1},
}
This package requires Julia >= v1.3.0
To install it, please run
] add BifurcationKit
To install the bleeding edge version, please run
] add BifurcationKit#master
Most plugins are located in the organization bifurcationkit:
- HclinicBifurcationKit.jl computation and bifurcation analysis of homoclinic / heteroclinic orbits of ordinary differential equations (ODE)
- DDEBifurcationKit.jl bifurcation analysis of delay differential equations (DDE)
- AsymptoticNumericalMethod.jl provides the numerical continuation algorithm Asymptotic Numerical Method (ANM) which can be used directly in
BifurcationKit.jl - GridapBifurcationKit.jl bifurcation analysis of PDEs solved with the Finite Elements Method (FEM) using the package Gridap.jl.
- PeriodicSchurBifurcationKit.jl state of the art computation of Floquet coefficients, useful for computing the stability of periodic orbits.
The list of capabilities is available here.