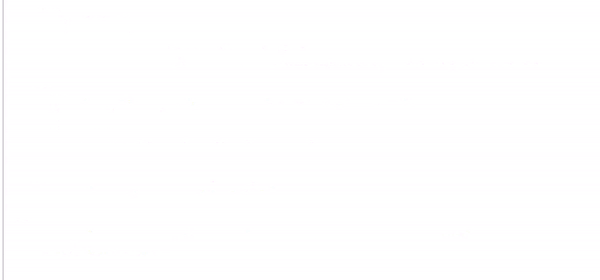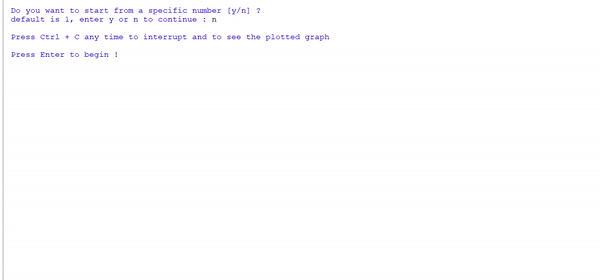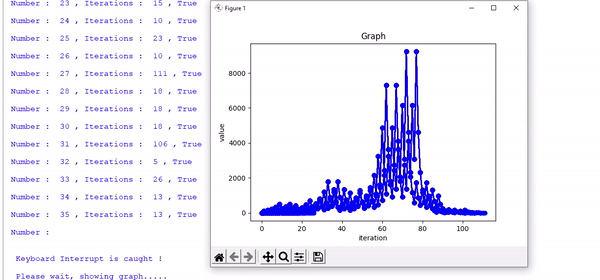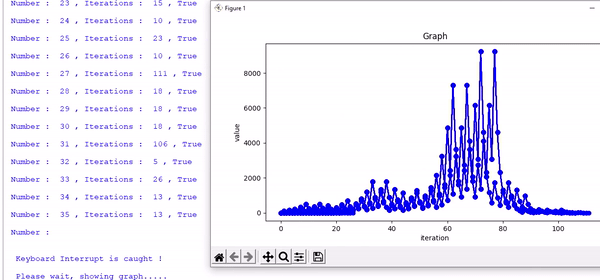The Collatz Conjecture or hailstone sequence is presented in an interactive computer programme to calculate the sequence.
The sequence is generated by starting with any positive whole number greater than zero and following two rules.
- If the number is odd, then multiply by three and add one ( x3+1)
- If the number is even, then divide by two (/2)
The sequence will continue till infinity due to its nature. However, the programme detects the lowest number in the series, which is 1 and stops.
It also shows values like, number of iterations and graph of the generated sequence.
Prerequisites:
- Your computer must be running Python3.9 or newer
- Below is the library that has been used to plot graphs, it should be installed before executing the programme
pip install matplotlib
Pick a number & Press enter 1 2 3 4 5 6 7 8 9... >>> 7
7 Good choice.
Press Enter to begin !
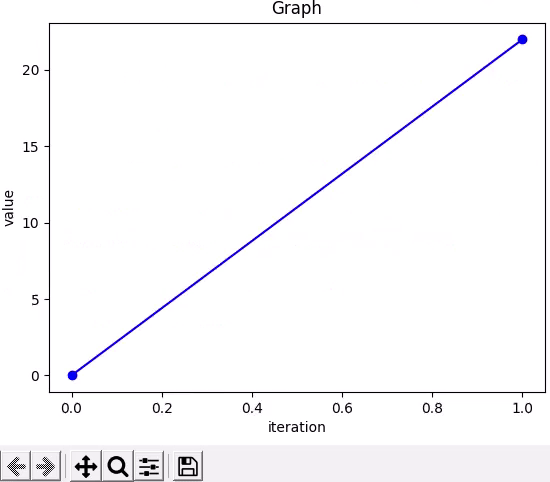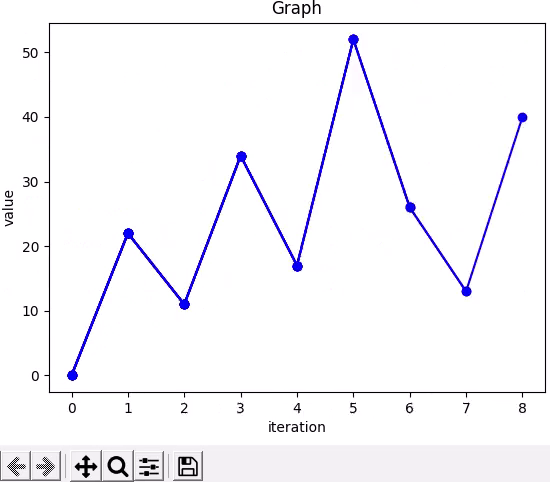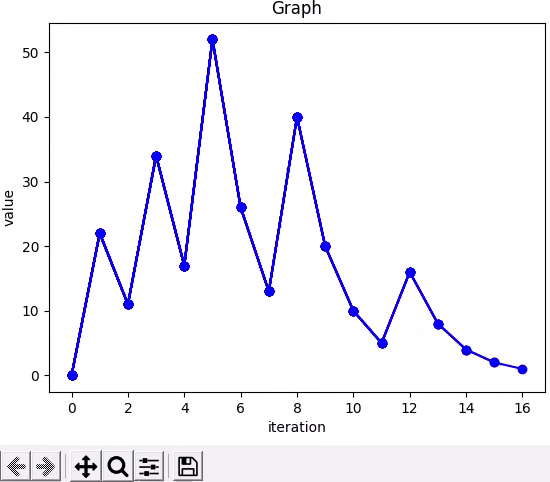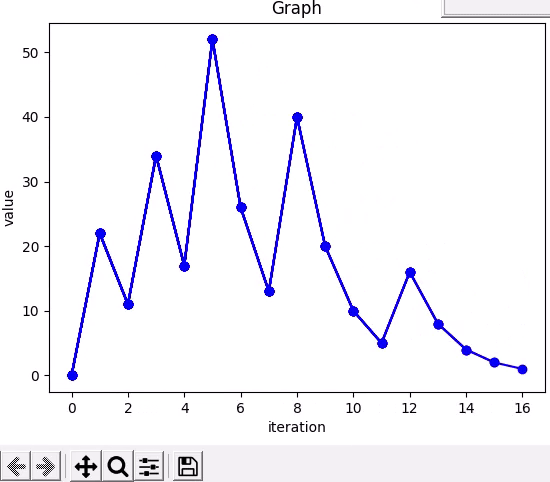
-> 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
Iterations : 16
The programme follows the rules and generates a sequence, where the lowest number is one.
The conjecture is: every positive integer, if you apply these rules, will eventually end up in the 4, 2, 1 loop.
Here, 1 is odd, multiply by three and add one.
Which equals 4.
Even, divide by two, 2, still even.
Divide by two, 1, odd.
So, 1 goes to 4, goes to 2, goes to 1.
We're in loop and the lowest number is 1.
This is Commonly called the Collatz conjecture, and the numbers obtained by applying 3x+1 are called hailstone numbers, because they go up and down like hailstones in a thundercloud, but eventually they all fall down to one.
In above demonstration the number is 7. In total, it takes 16 steps/iterations to get down to one, and end up in the four, two, one loop.
Now the paths that different numbers take vary so widely, below the graph shows the path of number seven.
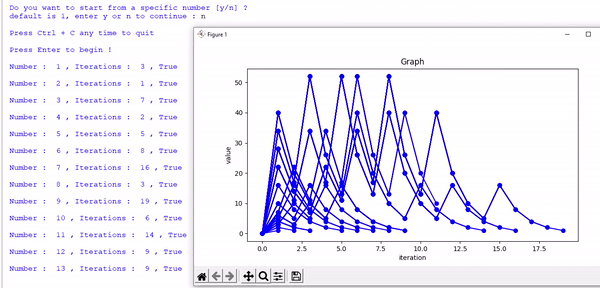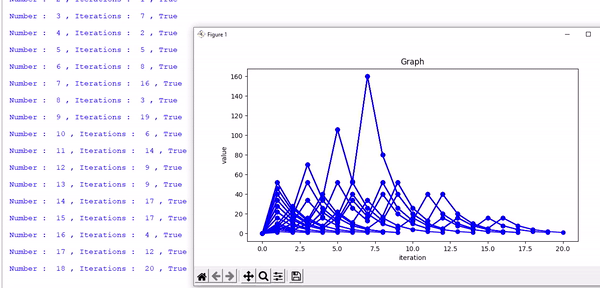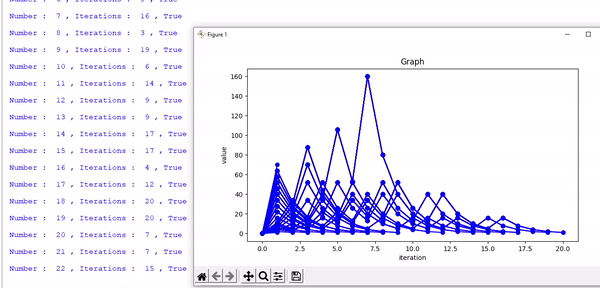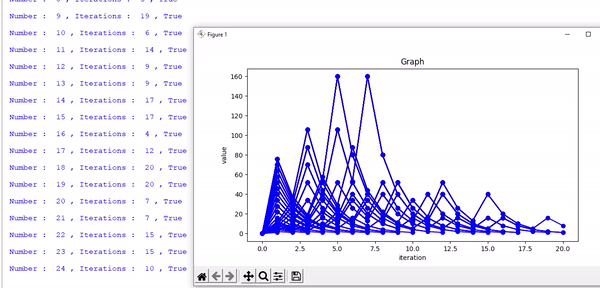
[ 1 ] The programme is written in a way that, it will loop itself to infinity.
It repeats indefinitely, going through all the possible positive whole number (1, 2, 3, 4.....) one after one, automatically once initiated.
It has all the features and follws the same rules for calculation and plot the graph of generated sequence live, also ask to the user whether to start from a given number or from default, which is 1.
If the number falls in the loop of 4, 2, 1 ,then it returns True.
If not then returns False ( not detected yet ) and will go to the next number.
The programme is a bit slow, and might slow down your computer.
Since it plots the graph of every single number simultaneously.
[ 2 ] This programme is an alternate version of the above infinite script.
It has all the features and follows the same rules for calculation and plot the graph of
generated sequence when it detects Keyboard Interrupt Ctrl+C.
The Programme is faster than the above script, since it does not plot graphs every single time, only when user commands it to plot.
[ 3 ] This programme has all the features except graph plotting, and follows the same rules for calculation.
The script is bit more faster than all the above scripts, since it does not plot graphs at all, only stops when the programme returns False or the Conjecture breaks.
[ 4 ] This programme has two additional features while still lacking graph plotting. The first feature is writing all numbers in a sequence to a text file, then checking that file each iteration. This allows an increase in speed by skipping numbers that have previously appeared in a sequence, as well as terminating a sequence that converges on a previous sequence. The second feature is that the programme will record numbers with a sequence of 1 or more to another text file, and then when the programm is run later, it will read the last sequence and start from the next number, allowing for continuous progress.
Feel free to report issues and contribute to this repository.
Copyright © Abhijeet Kumar. All rights reserved.
Licensed under the MIT License.