Physical Domain Reconstruction with Finite Volume Neural Networks

This repository contains the PyTorch code for models, training, testing, and Python code for data generation to conduct the experiments as reported in the works Inferring Boundary Conditions in Finite Volume Neural Networks and Physical Domain Reconstruction with Finite Volume Neural Networks.

Abstract

The finite volume neural network (FINN) is an exception amongst recent physics-aware neural network models as it allows the specification of arbitrary boundary conditions (BCs). FINN can generalize and adapt to various prescribed BC values not provided during training, where other models fail. However, FINN depends on explicitly given BC values and cannot deal with unobserved parts within the physical domain. To overcome these limitations, we extend FINN in two ways. First, we integrate the capability to infer BC values on-the-fly from just a few data points. This allows us to apply FINN in situations, where the BC values, such as the inflow rate of fluid into a simulated medium, is unknown. Second, we extend FINN to plausibly reconstruct missing data within the physical domain via a gradient-driven spin-up phase. Our experiments validate that FINN reliably infers correct BCs, but also generates smooth and plausible full-domain reconstructions that are consistent with the observable data. Moreover, FINN can generate precise predictions orders of magnitude more accurate compared to competitive pure ML and physics-aware ML models---even when the physical domain is only partially visible, and the BCs are applied at a point that is spatially distant from the observable volumes.

Keywords: Physics-aware neural networks · Boundary conditions · Retrospective inference · Partial differential equations · Inductive biases

Outline

This repository is a combination of two complementary papers. In the first one, we tested FINN's ability to infer unknown boundary conditions and compared its performence with two state-of-the-art models (DISTANA and PhyDNet). A detailed explanation of the experiments and results can be found in the papers. However, we add here some videos showing the results of the models to invoke an intuitive understanding of the results. Following videos show predictions by the models inferring the BCs of the data and predicting the Burgers' equation.


FINN	DISTANA	PhyDNet

Videos show clearly that FINN's performence outperforms the other models. In this experiments, the trained models infer only $2$ BCs (i.e. $2$ learnable parameters to optimize), that are set to $[4.0, -4.0]$. Please refer to Inferring Boundary Conditions in Finite Volume Neural Networks for an exhaustive exploration of BC inference.

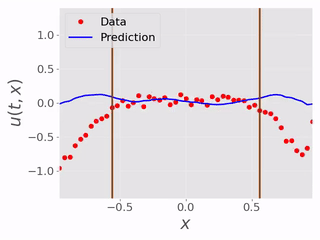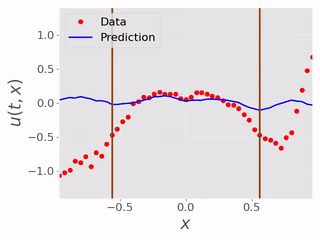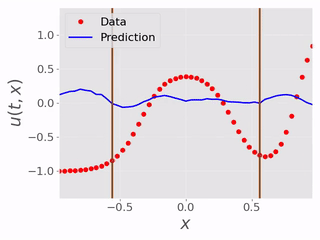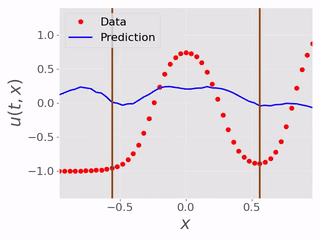
After testing the BC inference ability, we tested the performence of the models inferring the masked physical domain alongside the boundary conditions. Following are videos showing models inferring masked physical domain and boundary conditions with noisy data:


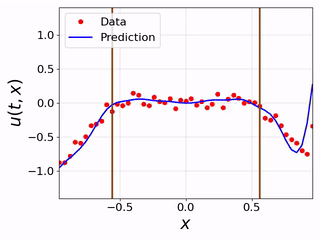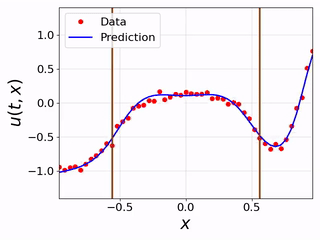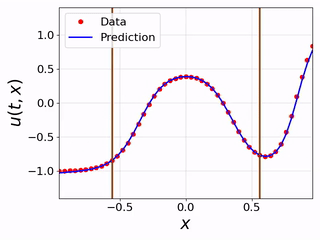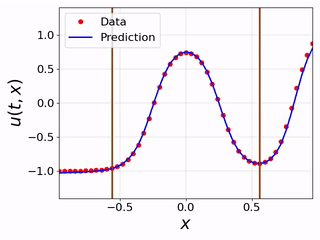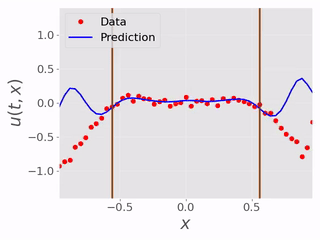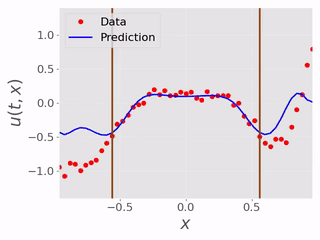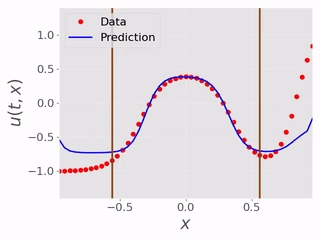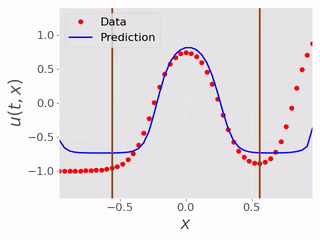FINN	DISTANA	PhyDNet

In this set of experiments there were in total of $51$ learnable parameters at inference. Interested in why $51$? Because we used an efficient retrospective inference method called active tuning. For more about the active tuning algorithm, the whole inference process and how to deal with noisy data you can check out Physical Domain Reconstruction with Finite Volume Neural Networks.

If you find this repository helpful, please cite our works:

@InProceedings{Horuz2022,
    author    = {Coşku Can Horuz and Matthias Karlbauer and Timothy Praditia and Martin V. Butz and Sergey Oladyshkin and Wolfgang Nowak and Sebastian Otte},
    booktitle = {International Conference on Artificial Neural Networks (ICANN)},
    title     = {Inferring Boundary Conditions in Finite Volume Neural Networks},
    year      = {2022},
    publisher = {Springer Nature Switzerland},
    isbn      = {978-3-031-15919-0},
    pages     = {538--549}
}

@article{Horuz2023,
    author = {Coşku Can Horuz and Matthias Karlbauer and Timothy Praditia and Martin V. Butz and Sergey Oladyshkin and Wolfgang Nowak and Sebastian Otte},
    title = {Physical Domain Reconstruction with Finite Volume Neural Networks},
    journal = {Applied Artificial Intelligence},
    volume = {37},
    number = {1},
    pages = {2204261},
    year  = {2023},
    publisher = {Taylor & Francis},
    doi = {10.1080/08839514.2023.2204261}
}

Dependencies

We recommend setting up an (e.g. conda) environment with python 3.7 (i.e. conda create -n finn python=3.7). The required packages for data generation and model evaluation are

conda install -c anaconda numpy scipy
conda install -c pytorch pytorch==1.9.0
conda install -c jmcmurray json
conda install -c conda-forge matplotlib torchdiffeq jsmin

Models & Experiments

The code of the pure machine learning model DISTANA and physics-aware models (PhyDNet and FINN) can be found in the models directory.

Each model directory contains a config.json file to specify model parameters, data, etc. Please modify the sections in the respective config.json files.

The actual models can be trained and tested by calling the according python train.py or python test.py scripts. Alternatively, python experiment.py can be used to either train or test n models (please consider the settings in the experiment.py script).

Data generation

The Python scripts to generate the burger and allen-cahn data can be found in the data directory. In each of these directories, a data_generation.py and simulator.py script can be found. The former is used to generate train, extrapolation (ext), or test data. For details about the according data generation settings of each dataset, please refer to the corresponding data sections in the first FINN paper.

AdaptiveAILab/finn-domain-inference