/regression-models_course-project

Primary LanguageR

Course Project Regression Models

Brief Analysis about Manual and Automatic Transmissions

Binder

Executive Summary

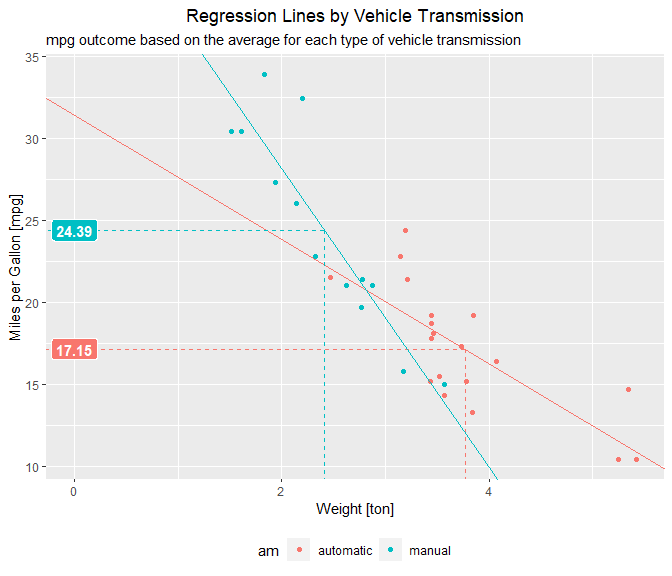
The data analysis process in this document has identified that manual vehicles have better performance than automatics concerning miles per gallon (mpg). Furthermore, based on this study’s linear regression model, the difference has reached 7.24 miles per gallon based on the average weights of automatic and manual cars (See Figure 4 in APPENDIX Section A4.), which is a significant number.

1. Introduction

The Motor Trend Car Road Test has evaluated 32 automobiles varying from 1973-74 models, and this study comprises fuel consumption, horsepower, weight, and other aspects. Based on it, the present publication aims to answer two questions:

  1. “Is an automatic or manual transmission better for MPG?”
  2. “Quantify the MPG difference between automatic and manual transmissions.”

2. Requeriments and Settings

If you are interested in reproducing this study, please visit the Github repository to have access to the raw document.

3. Loading Data and EDA

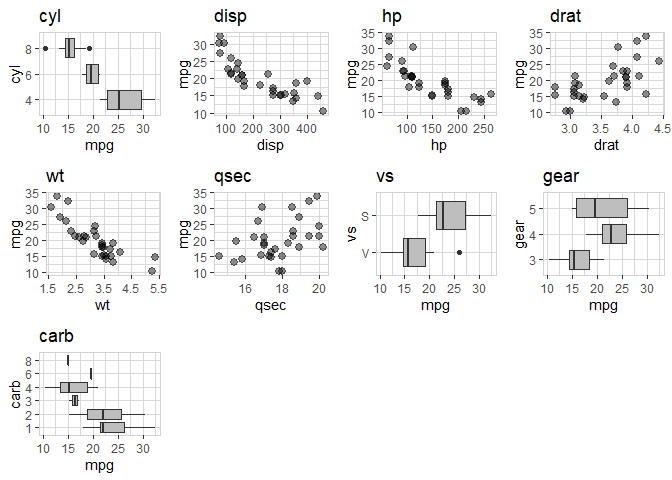
The adjusted data frame has 32 observations with no NA values, divided into 6 (six) numeric variables (no one is standardized or scaled) and 5 (five) categorical variables. For more exploratory details, please, find them in APPENDIX section A1. For more information about the variables descriptions, please, see it on the R Documentation website.

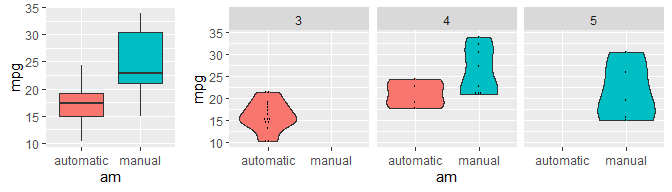
Due to Figure 2 in section A2 from APPENDIX, I have tested the hypothesis that the average consumption from automatic and manual vehicles is equal. In other words, H_O: \mu_{automatic} = \mu_{manual}, the p-value is 0.14% which is way less than alpha (5%). For this reason, the H_O was Rejected, which means the averages of automatic and manual transmissions are from different populations.

4. Model Selection

The model selection approach used for this project is based on the Week 3 videos and the Chapter Multiple variables and model selection from Regression Models for Data Science in R book.

4.1. Base line model

lm(formula = mpg \sim am, data = mtcars)

The baseline model is the Ordinary Linear Regression, and this model uses only transmission (am) to explain the consumption in miles per gallon (mpg). From the hypothesis tested in Section 3, this baseline model has identified that manual transmission performs better than automatic ones. On average, manual transmission yields 24.39 miles per gallon. On the other hand, automatic transmission yield 17.15 miles per gallon. The difference is 7.24 miles per gallon.

4.2. Analysis of Variance

Using the anova() function, it was possible to run several combinations, reaching the final model using am, wt, and interaction between am and wt.

lm(formula = mpg \sim am + wt + am \cdot wt, data = mtcars)

I have decided to use a simpler model due to the parsimony. The R2 adjusted has reached 81.51%. All p-values of the model are below alpha (5%).

The linear model coefficients:

Estimate Std. Error t value Pr(\>\|t\|)
(Intercept) 31.416055 3.0201093 10.402291 0.0000000
ammanual 14.878422 4.2640422 3.489276 0.0016210
wt -3.785907 0.7856478 -4.818836 0.0000455
ammanual:wt -5.298361 1.4446993 -3.667449 0.0010171

5. Residual Analysis

Due to the low number of observations, below 50, I have used the Shapiro-Wilk test to ensure the residual’s normality. The p-value obtained from this test was 8.72%, sufficient to reject the null hypothesis and proving the residual’s normality.

The residual analysis will be based on Figure 3 in APPENDIX Section A3.. This figure aims to corroborate the following explanations:

  • Residual vs. Fitted: The residual bounces around zero, which suggests an excellent linear relationship. Also, the residual is a homogeneous spread on the plot showing that the variance is “constant” in addition, I have identified no outlier.
  • Normal Q-Q: Most of the data is around the line, except in the top right of the chart. I did not identify any issue related to non-normality.
  • Scale-Location: There are no patterns in the points, the data stay between a fixed band, and the red line is almost constant. From those characteristics, the residual is considered homoscedasticity.
  • Residual vs. Leverage: No points above the dotted line means there is no influential high point.

6. Conclusion

Considering the baseline model, the am variable can explain 33.85% of the miles per gallon. However, In the final model, the percentage of variance explained by the model rises to 81.51% with the inclusion of two more predictors (wt and interaction of wt and am).

  • Final model:

mpg= \begin{cases} \text{Automatic vehicle (am = 0)} \implies \beta_0 + \beta_2 \cdot wt = 31.42 -3.79 \cdot wt \\ \text{Manual vehicle (am = 1)} \implies (\beta_0 + \beta_1) + (\beta_2 + \beta_3) \cdot wt = 46.29-9.08 \cdot wt \end{cases}

APPENDIX

A1. Exploratory Data Analysis

Figure 1 – Exploratory Data Visualization

A2. Miles per Galon (mpg) vs Transmission (am)

Figure 2 – Fuel Consumption divided into Transmission and number of Gears.

A3. Residuals

Figure 3 – Residuals.

A4. Regression Lines

Figure 4 – On average, a manual car yields 7.24 more miles per gallon than automatics.