Customizable Decision Tree

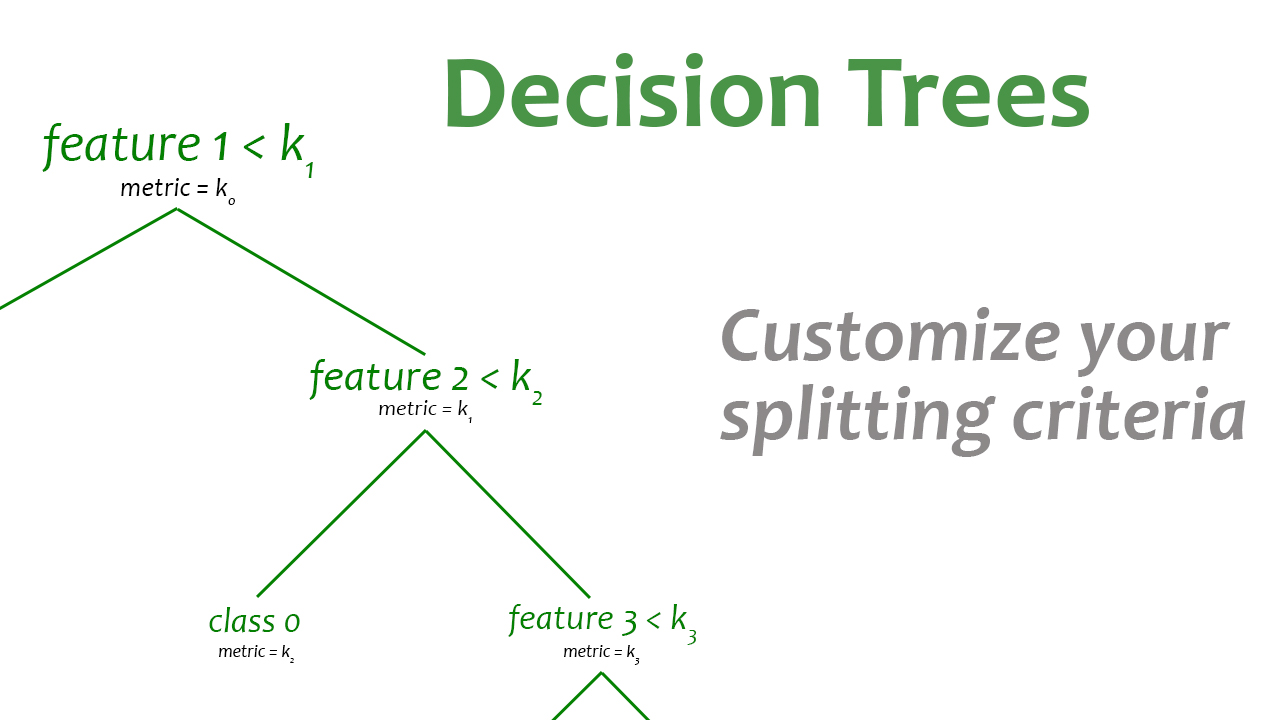
This repository enables the creation of decision trees and random forests with customized splitting criteria, thus allowing the user to optimize the model for a specific problem. This tool provides the flexibility to define a metric that best suits the problem at hand, for example popular classification metrics like F1 score and recall, as well as more specific metrics such as economic profit or any user-defined cost function.

This underused area of metric selection is particularly effective in "cost-dependent" scenarios and can lead to significant improvements in results.

Examples of use

Here are a few examples of how a custom splitting criteria can be useful:

In a trading movements classification (up or down) where the goal is to maximize economic profit, the tool can be used to specify the metric as being equal to the economic profit. The tree splitting will be optimized based on this metric.
In a churn prediction scenario, where the objective is to minimize the number of false negatives, F1 score or recall may be used as the splitting criterion.
In a fraud detection scenario, the tool can be used to optimize the tree splitting based on the ratio of fraudulent transactions identified to the total number of transactions, rather than simply the number of correctly classified transactions.
In a marketing campaign, the tool can be used to optimize the tree splitting based on the expected revenue generated from each potential customer segment identified by the tree.

Reminder on splitting criteria

Typically, classification trees are constructed using a splitting criterion that is based on a measure of impurity or information gain.

Let us consider a 2-class classification using the Gini index as metric. The Gini index represents the impurity of a group of observations based on the proportion of observations in each class 0 and 1 :

$$ I_{G} = 1 - p_0^2 - p_1^2 $$

Since the Gini index is an indicator of impurity, partitioning is done by minimising the weighted average of the index in the child nodes $L$ and $R$. This is equivalent to minimising $\Delta$ :

$$ \Delta = \frac{N_t}{N} \times (I_G - \frac{N_{t_L} * I_{G_L}}{N_t} - \frac{N_{t_R} * I_{G_R}}{N_t}) $$

At each node, the tree algorithm finds the split that minimizes $\Delta$ over all possible splits and over all features. Once the optimal split is selected, the tree is grown by recursively applying this splitting process to the resulting child nodes.

Example

To integrate a specific metric, the user must define the get_metric function with a single argument representing the variables used in the metric calculation. By default, the metric is the Gini index.

For example, if the goal is to minimize the cost of occurrence of class 0 and 1 such that each cost is specific to each observation, the metric can be defined as:

import custom_tree

def get_metric(metric_vars):

    y = metric_vars[:, 0]
    cost0 = metric_vars[:, 1]
    cost1 = metric_vars[:, 2]

    proba1 = np.sum(y == 0) / len(y)
    proba1 = np.sum(y == 1) / len(y)
    metric = np.sum(proba0 * cost0) + np.sum(proba1 * cost1)

    return metric

custom_tree.get_metric = get_metric

Training the model CustomDecisionTreeClassifier or CustomRandomForestClassifier. The user should specify the optimisation method parameter according to the metric (split should be done by minimising/maximising the metric):

model = custom_tree.CustomDecisionTreeClassifier(max_depth=2)
model.fit(X=X, y=y, metric_vars=costs, optimisation_method='minimisation')

Getting predicted probabilites for each class with the possibility to return the expected metric in the predicted leaf:

probas = model.predict_proba(X=X, return_exp_metric=True)
probas[:5]

>> [([0.32, 0.68], 462),
    ([0.26, 0.74], 165),
    ([0.10, 0.90], 151),
    ([0.10, 0.90], 151),
    ([0.32, 0.68], 462)]

Printing the tree:

model.print_tree(max_depth=2, features_names=None, 
                 show_delta=False, show_metric=True, show_repartition=False)

>> |     --- node 1 -> metric = 1385
   |     |     --- node 2 | feature 0 <= 5.9 -> metric = 664
   |     |     |     --- node 4 | feature 2 <= 4.1 -> metric = 462
   |     |     |     --- node 5 | feature 2 > 4.1 -> metric = 151
   |     |     --- node 3 | feature 0 > 5.9 -> metric = 570
   |     |     |     --- node 6 | feature 0 <= 6.0 -> metric = 165
   |     |     |     --- node 7 | feature 0 > 6.0 -> metric = 302

Extra

The function that calculates $\Delta$ can also be specified by the user if required. By default, this function is defined as:

def get_delta(split, metric_vars, optimisation_method='minimisation'):

    delta =  get_metric(metric_vars) - (get_metric(metric_vars[split]) + get_metric(metric_vars[np.invert(split)]))

    if optimisation_method == 'maximisation':
        delta = - delta

    return delta

Current limitations

The library has, for now, the following limitations :

Only 2-class classification is supported
Feature importance is not supported
Split computation and decision trees computation are not parallelized

Credits

This repository is maintained by Antoine PINTO (antoine.pinto1@outlook.fr).