QIdris

A Quantum simulator built in Idris 2.

Description

This project is a quantum simulator built in Idris 2. It is a work in progress and is not yet complete. The goal is to build a quantum simulator that can simulate quantum circuits and quantum algorithms with type safety via quantitative type theory.

Documentation

The documentation for this project can be found here

Example

Small examples can be found here

-- Define a quantum program that takes in a circuit of 2 qubits
-- 2 qubits = 4 possible states
-- The input matrix is a linear type to prevent copy bugs
prog : QCircuit 4
prog initial = do 
    let result = initial
          |> (H >< ID) -- Put the first qubit in superposition (and identity on second)
          |> CNOT      -- If the first bit is true, flip the second bit (entangles the two bits)

    -- Return the final state
    finish result

main : IO ()
main = do 
    -- Create initial state (both bits set to 0 by default)
    let initial = zero >< zero
    
    result <- runCircuit initial prog
    let probs  = result * result -- Square state vec to get probabilities

    -- Print the probabilities of each state
    putStrLn "Probabilities: "
    putStrLn "-------------------"
    printStateVec result
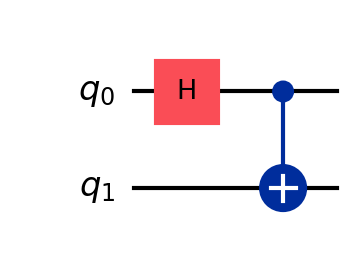
    printStateVec probs

Explanation

The above code defines a quantum program that takes in a quantum circuit of 2 qubits and returns a quantum circuit of 2 qubits. The program puts the first qubit in superposition, then entangles the two qubits by flipping the second qubit if the first qubit is true. The probabilities of each state are then printed. It is equivalent to the following quantum circuit:

Output

Probabilities: 
-------------------
|00> : [0.7071067811865475]
|01> : [0.0]
|10> : [0.0]
|11> : [0.7071067811865475]

|00> : [0.4999999999999999]
|01> : [0.0]
|10> : [0.0]
|11> : [0.4999999999999999]

Here, the output shows that the result of the quantum program is a superposition of the states |00> and |11> with equal probabilities.

Composition of Quantum Circuits

One problem with quantum computing in general is that it's difficult to abstract actions on qubits. In this implementation, Quantum Circuits are represented as monads, which allows for easy composition of quantum circuits. For example, let's define a custom operation that applies the hadamard to the first qubit and applies the controlled NOT gate to the second qubit:

myOperation : (1 q : QSystem 4) -> QSystem 4 
myOperation initial = initial |> (H >< ID) |> CNOT

Now, let's define a custom operation which performs the previously defined operation twice:

myOperation : (1 q : QSystem 4) -> QSystem 4
myOperation initial = initial |> (H >< ID) |> CNOT

myOperationTwice : (1 q : QSystem 4) -> QSystem 4
myOperationTwice = myOperation . myOperation

(NOTE: Data.Linear needs to be imported for function composition not throw a type error).

It's important to note that because the operations were defined as pure functions operating on quantum systems, they cannot non-deterministically measure the qubits. If you want compositions of quantum operations that can measure qubits, you can use the monadic bind operator to combine these operations. For example:

myOperation : QCircuit 4
myOperation initial = measure (initial |> (H >< ID) |> CNOT)

myOperationTwice : QCircuit 4
myOperationTwice initial = myOperation initial >>= myOperation