Parallel Implementation of LU decomposition

###Basics

Root directory contains three sub-directories namely ’Sequential’, ’OpenMP’ and ’MPI’.
Each subdirectory has source code in the form of ** ’*.c’** file.
Matrix is generated in a manner that it decomposes into a L and U containing only 1s and 0s.
To submit jobs for various configurations run ’./submit.sh’ on terminal. This will automatically submit all the jobs in the subdirectory to the general-compute queue of the ccr cluster.
Outputs are generated in the output.txt file. Sample outputs are included.
In the corresponding subdirectory run ./plot.sh on the linux terminal to generate a graphical visualization of the output. gnuplot is required to generate graph.
Graphs are generated as ’Plot.pdf’. Please wait for the job run to finish and outputs to accumulate.

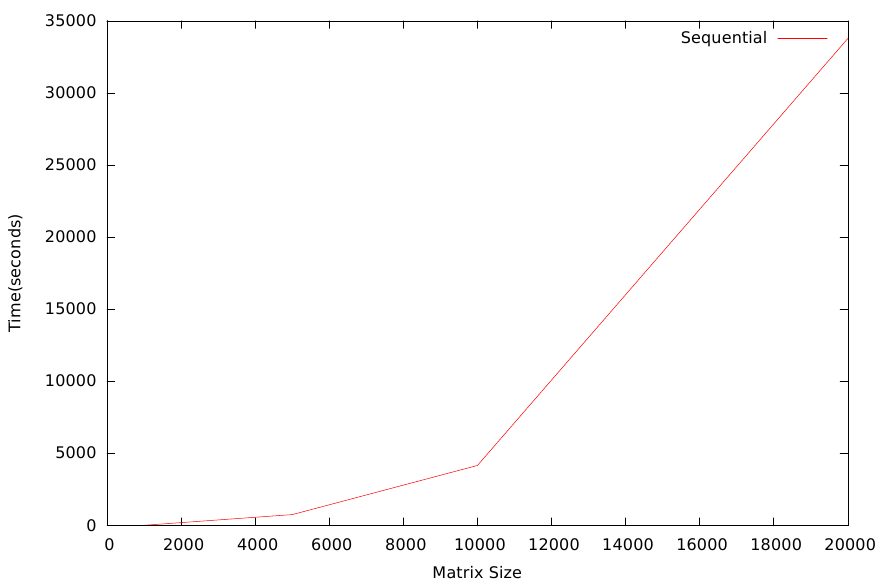
Gaussian elimination algorithm was implemented that sequentially decomposes the square matrix.
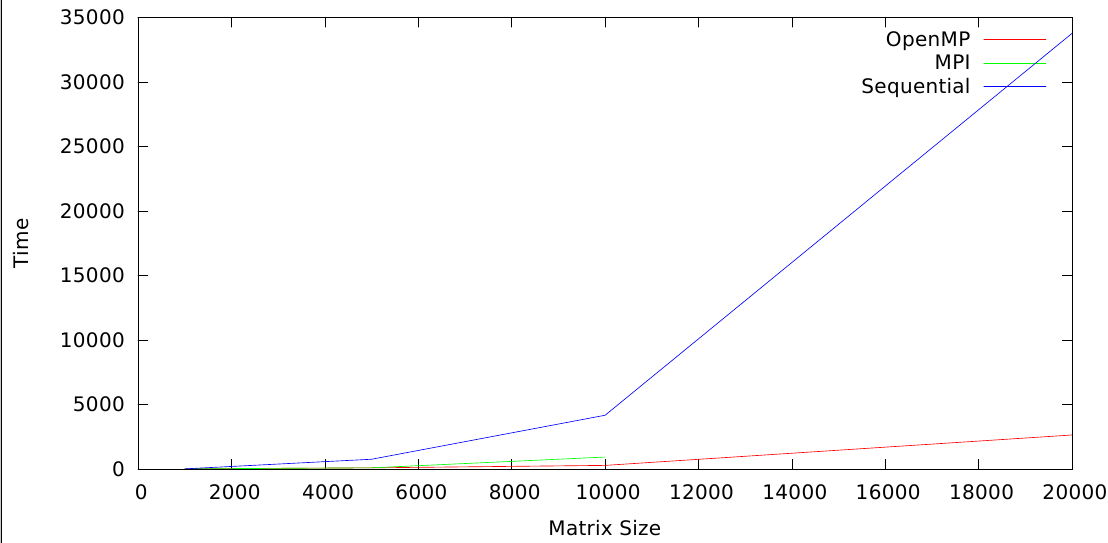
Algorithm was evaluated on input matrix size of 1000, 5000, 10000, 20000.
Time taken to decompose the matrix grew exponentially with the increase in size.
Since, this was a sequential implementation increase in compute nodes won’t do anything.
Since I was using Gaussian elimination that computes L and U matrices separately, I ran out of memory when matrix size of 50,000 was tried. This implementation makes two copies of the matrix of same size as input.

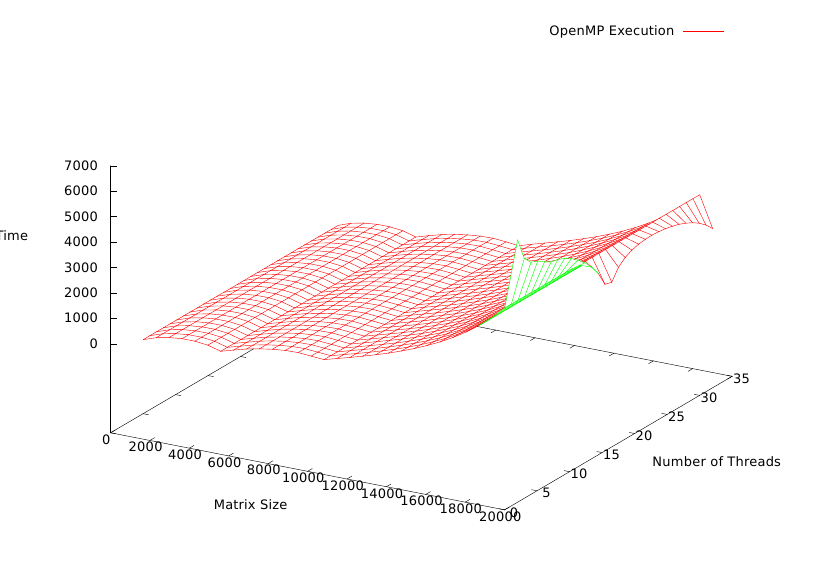
Gaussian elimination algorithm was implemented that uses the block wise decomposition in parallel.
The for loops are parallelized in a manner that blocks of matrices are decomposed by dividing the work among parallel threads.
Algorithm was evaluated for input matrix of sizes 1000, 5000, 10000, 20000 with a combination of 2, 4, 8, 16, 32 threads executing in parallel.
On a fixed workload the decompostion was faster when more threads are executing in parallel. The execution was comparatively faster on larger workload due to the fact, parallelism was more effective.
For a fixed number of cores the time increased exponentially with increase in matrix size.
The parallelism was ineffective on relatively smaller loads.
Since I was using Gaussian elimination that computes L and U matrices separately, I ran out of memory when matrix size of 50,000 was tried. This implementation makes two copies of the matrix of same size as input.

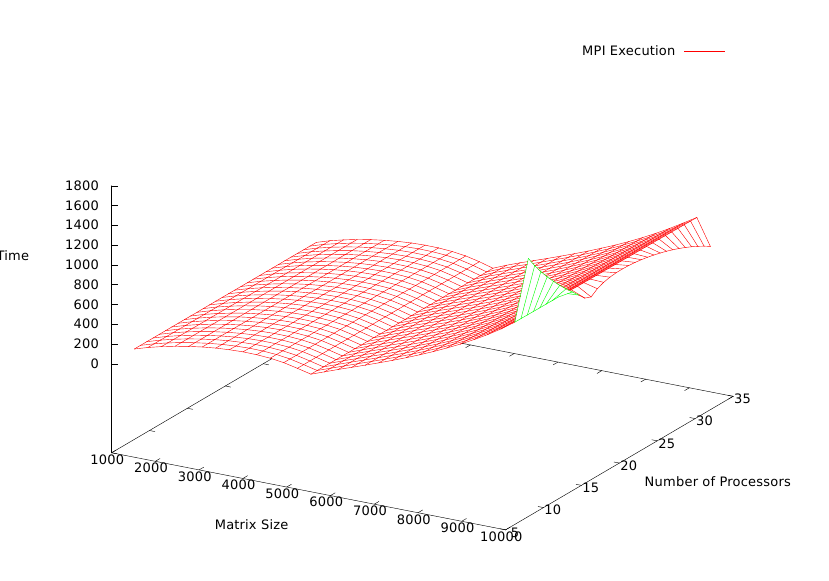
Cyclic distribution was used to accomplish LU factorization of the input square matrix.
Each node is responsible for computing its own block and broadcast the result to rest of the nodes.
Algorithm was evaluated for input matrix of sizes 1000, 5000, 10000 with a combination of 8, 16, 32 compute nodes working in parallel.
For a fixed number of compute nodes the algorithm showed uniform behavior.
For fixed workload the parallelism was more effective for larger workloads on maximum compute nodes.

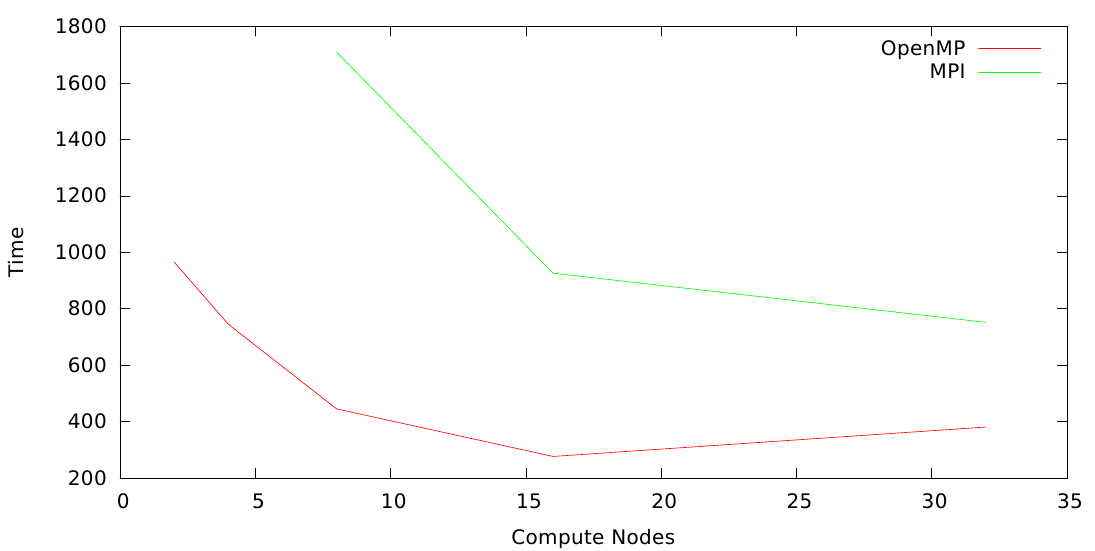
Since, MPI involves communication overhead between different nodes, it was slower as compared to OpenMP.
As expected sequential algorithm turns out to be the worst performer of the three.

LU factorization algorithm has a great extent of parallelization when scaled appropriately.