We propose a new framework of CatBoost that predicts the entire conditional distribution of a univariate response variable. In particular, CatBoostLSS models all moments of a parametric distribution, i.e., mean, location, scale and shape (LSS), instead of the conditional mean only. Choosing from a wide range of continuous, discrete and mixed discrete-continuous distributions, modelling and predicting the entire conditional distribution greatly enhances the flexibility of CatBoost, as it allows to gain additional insight into the data generating process, as well as to create probabilistic forecasts from which prediction intervals and quantiles of interest can be derived. In the following, we provide a short walk-through of the functionality of CatBoostLSS.
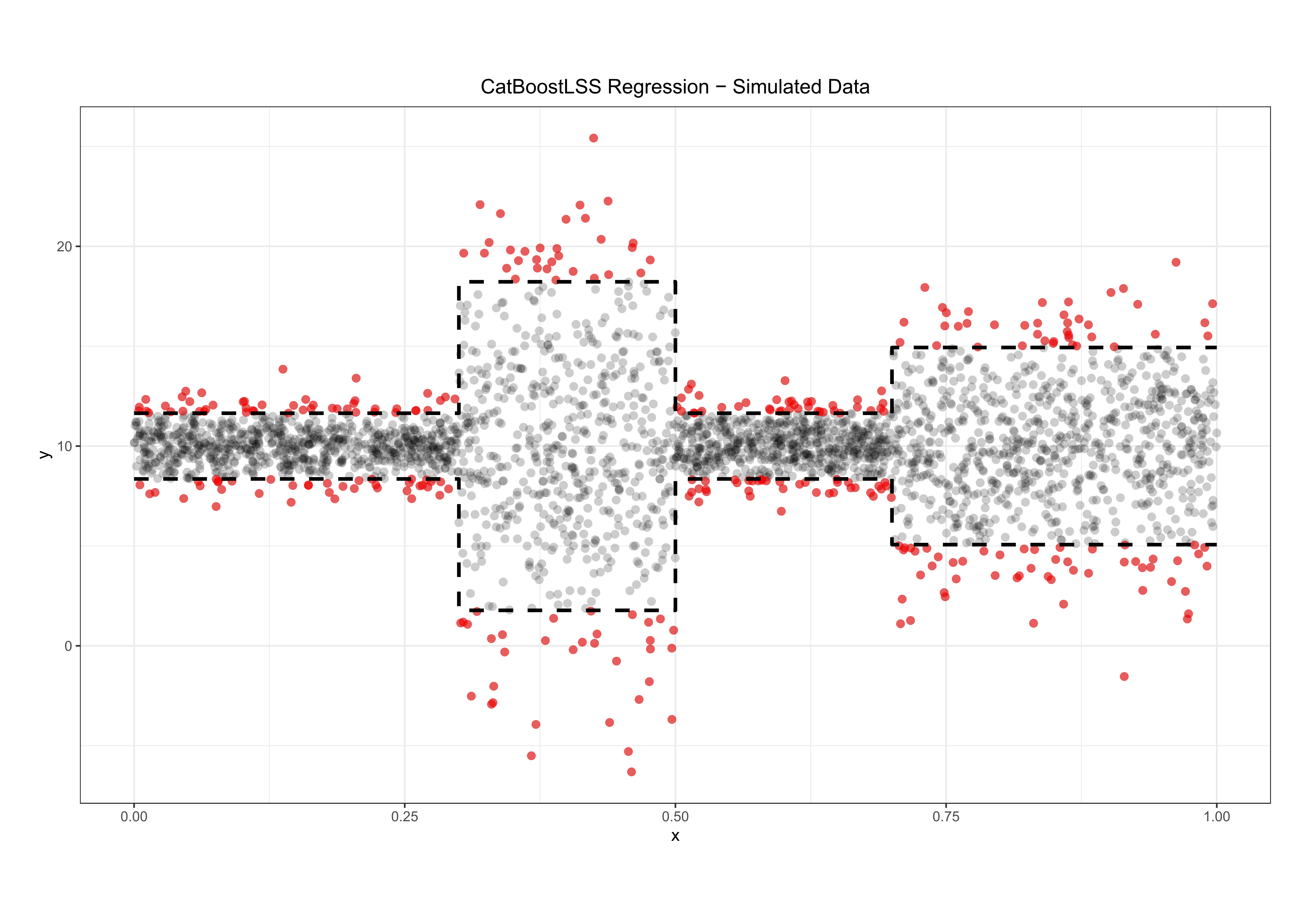
We start with a simulated a data set that exhibits heteroscedasticity where the interest lies in predicting the 5% and 95% quantiles. Details on the data generating process can be found here. The dots in red show points that lie outside the 5% and 95% quantiles, which are indicated by the black dashed lines.
Let's fit a CatBoostLSS to the data. In general, the syntax is similar to the original CatBoost implementation. However, the user has to make a distributional assumption by specifying a family in the function call. As the data has been generated by a Normal distribution, we use the Normal as a function input.
# Import library
from catboostlss import *
import shap
# Data for CatBoostLSS
train_cblss = Pool(data = train_data,
label = train_labels,
has_header = True)
test_cblss = Pool(data = test_data,
label = test_labels,
has_header = True)
# Fit model
cblss = CatBoostLSSRegressor(family = "NO",
leaf_estimation_method = "Newton",
logging_level = "Silent",
random_seed = 123,
thread_count = -1)
cblss.fit(train_cblss)As CatBoost yields state-of-the-art prediction results without extensive data training typically required by other machine learning methods, we estimate the model with its default parameter settings. Once the model is trained, we can predict all parameters of the distribution.
preds_cblss = cblss.predict(test_cblss, param = "all") As CatBoostLSS allows to model the entire conditional distribution, we can draw random samples from the predicted distribution, which allows us to create prediction intervals and quantiles of interest. The below image shows the predictions of CatBoostLSS for the 5% and 95% quantile in blue.
The great flexibility of CatBoostLSS also comes from its ability to provide attribute importance, as well as partial dependence plots for all of the distributional parameters. In the following we only investigate the effect on the conditional variance. The following plots are generated using wrappers around the SHAP (SHapley Additive exPlanations) package.
The plot of the Shapley value shows that CatBoostLSS has identified the only informative predictor x and does not consider any of the noise variables X1, ..., X10 as an important feature. Looking at partial dependence plots of the effect of x on Var(y|x) shows that it also correctly identifies the amount of heteroscedasticity in the data.
In this example we show the usage of CatBoostLSS using a sample of 2,053 apartments from the data collected for the preparation of the Munich rent index 2003.
The first decision one has to make is about choosing an appropriate distribution for the response. As there are many potential candidates, we use an automated approach based on the generalised Akaike information criterion.
dist GAIC
1 GB2 6588.29
2 NO 6601.17
3 GG 6602.02
4 BCCG 6602.26
5 WEI 6602.37
6 exGAUS 6603.17
7 BCT 6603.35
8 BCPEo 6604.26
9 GA 6707.85
10 GIG 6709.85
11 LOGNO 6839.56
12 IG 6871.12
13 IGAMMA 7046.50
14 EXP 9018.04
15 PARETO2 9020.04
16 GP 9020.05Even though the generalized Beta type 2 provides the best approximation to the data, we use the more parsimonious Normal distribution, as it has only two distributional parameter, compared to 4 of the generalized Beta type 2. In general, though, CatBoostLSS is flexible to allow the user to choose from a wide range of continuous, discrete and mixed discrete-continuous distributions. Now that we have specified the distribution, let's fit our CatBoostLSS to the data. Again, we use the default parameter settings without tuning the parameters.
# Data for CatBoostLSS
train_cblss = Pool(data = train_data,
label = train_labels,
has_header = True)
test_cblss = Pool(data = test_data,
label = test_labels,
has_header = True)
# Fit model
cblss_rent = CatBoostLSSRegressor(family = "NO",
leaf_estimation_method = "Newton",
logging_level = "Silent",
random_seed = 123,
thread_count = -1)
cblss_rent.fit(train_cblss)Looking at the estimated effects indicates that newer flats are on average more expensive, with the variance first decreasing and increasing again for flats built around 1980 and later. Also, as expected, rents per square meter decrease with an increasing size of the appartment.
The diagnostics for CatBoostLSS are based on quantile residuals of the fitted model. Quantile residuals are based on the idea of inverting the estimated distribution function for each observation to obtain exactly standard normal residuals.
CatBoostLSS provides a well calibrated forecast and the good approximation of our model to the data is confirmed. CatBoostLSS also allows to investigate the estimated effects for all distributional parameter. Looking at the top 10 Shapley values for both the conditional mean and variance indicates that both yearc and area are considered as being important variables.
To get a more detailed overview of which features are most important for our model, we can also plot the SHAP values of every feature for every sample. The plot below sorts features by the sum of SHAP value magnitudes over all samples, and uses SHAP values to show the distribution of the impacts each feature has on the model output. The color represents the feature value (red high, blue low). This reveals for example that newer flats increase rents on average.
# Gloabl Shapley values for E(y|x)
shap.initjs()
mu_explainer = shap.TreeExplainer(cblss_rent, param = "mu")
shap_values_mu = mu_explainer.shap_values(test_cblss)
shap.summary_plot(shap_values_mu, test_data)Besides the global attribute importance, the user might also be interested in local attribute importances for each single prediction individually. This allows to answer questions like 'How did the feature values of a single data point affect its prediction?' For illustration purposes, we select the first predicted rent of the test data set.
# Local Shapley value for E(y|x)
shap.force_plot(mu_explainer.expected_value, shap_values_mu[1], test_data[:1])We can also visualize the test set predictions.
shap.force_plot(mu_explainer.expected_value, shap_values_mu, test_data)As we have modelled all parameter of the Normal distribution, CatBoostLSS provides a probabilistic forecast, from which any quantity of interest can be derived. The following plot shows a subset of 50 predictions only for ease of readability. The red dots show the actual out of sample rents, while the boxplots are the distributional predictions.
Also, we can plot a subset of the forecasted densities and cumulative distributions.
To evaluate the prediction accuracy of CatBoostLSS, we compare the forecasts of the Munich rent example to the implementations available in XGBoostLSS, gamlss, gamboostLSS, bamlss, disttree and NGBoost. We evaluate distributional forecasts using the average Continuous Ranked Probability Scoring Rules (CRPS) and the average Logarithmic Score (LOG), where lower scores indicate a better forecast, along with additional error measures evaluating the mean-prediction accuracy of the models. Recall that we use the default parameter setttings for CatBoostLSS, while all other models are trained using tuned parameters. Further details on how we trained the models can be found here. NGBoost is trained with the following manually selected parameters, as there is no built-in parameter tuning available yet
np.random.seed(seed = 1234)
ngb = NGBoost(Base = default_tree_learner,
Dist = Normal,
Score = MLE(),
n_estimators = 200,
learning_rate = 0.03,
natural_gradient = True,
minibatch_frac = 0.7,
verbose = False)
ngb.fit(train_data, train_labels)
Y_preds = ngb.predict(test_data)
Y_dists = ngb.pred_dist(test_data)All measures show that CatBoostLSS provides a competetive forecast using default parameter setttings. However, it is important to stress that all available parameter-tuning approaches implemented in CatBoost (e.g., early stopping, CV, etc.) are also available for CatBoostLSS.
CRPS_SCORE LOG_SCORE MAPE MSE RMSE MAE MEDIAN_AE RAE RMSPE RMSLE RRSE R2_SCORE
CatBoostLSS 1.1562 2.1635 0.2492 4.0916 2.0228 1.6129 1.3740 0.7827 0.3955 0.2487 0.7784 0.3942
XGBoostLSS 1.1415 2.1350 0.2450 4.0687 2.0171 1.6091 1.4044 0.7808 0.3797 0.2451 0.7762 0.3975
gamboostLSS 1.1541 2.1920 0.2485 4.1596 2.0395 1.6276 1.3636 0.7898 0.3900 0.2492 0.7848 0.3841
GAMLSS 1.1527 2.1848 0.2478 4.1636 2.0405 1.6251 1.3537 0.7886 0.3889 0.2490 0.7852 0.3835
BAMLSS 1.1509 2.1656 0.2478 4.1650 2.0408 1.6258 1.3542 0.7890 0.3889 0.2490 0.7853 0.3833
DistForest 1.1554 2.1429 0.2532 4.2570 2.0633 1.6482 1.3611 0.7998 0.3991 0.2516 0.7939 0.3697
NGBoost 1.1634 2.2226 0.2506 4.2136 2.0527 1.6344 1.3574 0.7932 0.3950 0.2507 0.7899 0.3761While CatBoostLSS require to specify a parametric distribution for the response, it may also be useful to completely drop this assumption and to use models that allow to describe parts of the distribution other than the mean. This may in particular be the case in situations where interest does not lie with identifying covariate effects on specific parameters of the response distribution, but rather on the relation of extreme observations on covariates in the tails of the distribution. This is feasible using Expectile Regression. Plotting the effects across different expectiles allows the estimated effects, as well as their strengths, to vary across the response distribution.
In summary, CatBoostLSS has the following key features:
- Extends CatBoost to probabilistic forecasting from which prediction intervals and quantiles of interest can be derived.
- Valid uncertainty quantification of forecasts.
- High interpretability of results.
- Compatibility for training large models using large datasets (> 1 Mio rows).
- Low memory usage.
- Missing value imputation.
In its current implementation, CatBoostLSS is available in Python and the code will be made available soon.
März, Alexander (2019) "CatBoostLSS - An extension of CatBoost to probabilistic forecasting".