Before the concept of arrays was introduced, there was no straightforward way to group and access multiple data elements easily and efficiently.
Programmers used other data structures or manual techniques to store multiple elements.
EX: used complex technique like pointers to link data items together, which was difficult and error-prone.
- Most common approach using separate variables: Programmers would declare individual variables for each element they wanted to store.
For example, if they wanted to store five integers, they would create five variables like this:
int num1 = 10;
int num2 = 20;
int num3 = 30;
int num4 = 40;
int num5 = 50;
This method becomes cumbersome, impractical and error-prone when dealing with a large number of elements.
-
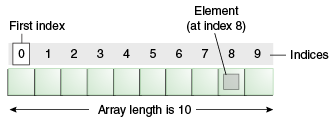
An array is a container object that holds a fixed number of values of a single type.
-
The length of an array is established when the array is created.
-
After creation, its length is fixed.
-
Each item in an array is called an element.
-
Each element is accessed by its numerical index.
1-Declaration and Initialization:
- To create an array, you first declare its type and then initialize it.
- The syntax for declaring an array is:
dataType[ ] arrayName; <br>
Ex: int [ ] numbers; <br>
- Initialize the array with a specific size, you use the new keyword:
numbers = new int[9]; // Creates an array of size 9 to store integers.
- You can initialize an array with values at the time of declaration, using curly braces:
Int[ ] numbers = {10, 20, 30, 40, 50};
2- Indexing:
- Array elements are accessed using zero-based indexing.
- The first element is at index 0, the second at index 1, and so on.
- To access an element, you use square brackets with the index inside:
int element = numbers[2]; // Accesses the third element (index 2) of the array
3- Length:
- Every array has a length property, which represents the number of elements it can store. You can retrieve the length using arrayName.length:
int size = numbers.length; // Retrieves the size of the 'numbers' array
4- iterating:
- Java offers a convenient way to iterate through the elements of an array
for (int i = 0; i < arrayName.length; i++) {
// Do something with arrayName[i]
}
// Enhanced for-loop (for-each loop)
for (dataType element : arrayName) {
// Do something with 'element'
}
5- Operations: storing a collection of data, searching, deleting, and more.
int [] numbers = new int[5]; //way1
int[] nums = {10, 20, 30, 40, 50}; //way2
System.out.println(numbers.length);
System.out.println(nums.length);
numbers[0] =3;
numbers[1] =4;
numbers[2] =5;
numbers[3] =6;
numbers[4] =7;
nums[2]= 60;
System.out.println(nums[2]);
-
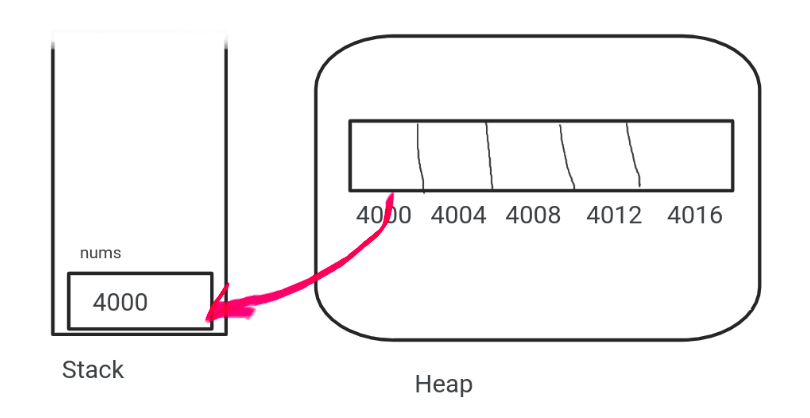
The elements in an array are stored in contiguous memory locations, making it efficient for accessing and manipulating elements.
-
This means that each element of the array is stored in a contiguous block of memory, with the first element stored at the lowest memory address and the last element stored at the highest memory address.
-
This allows for efficient access to the elements of the array, as it is possible to calculate the memory address of a particular element using a simple mathematical formula based on the array's starting address and the index of the element.
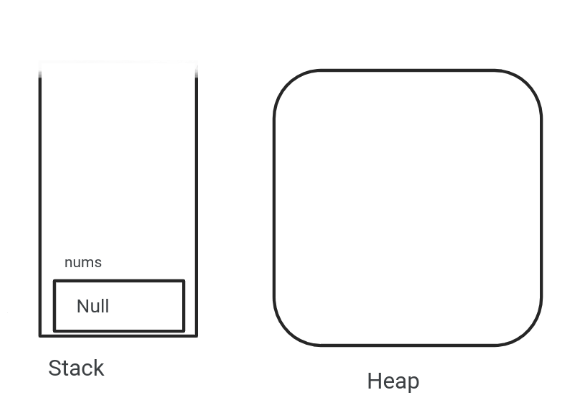
As we said before the memory is managed two areas (Stack , Heap)
Int [] nums;This will create a variable in the stack and has value null by default.
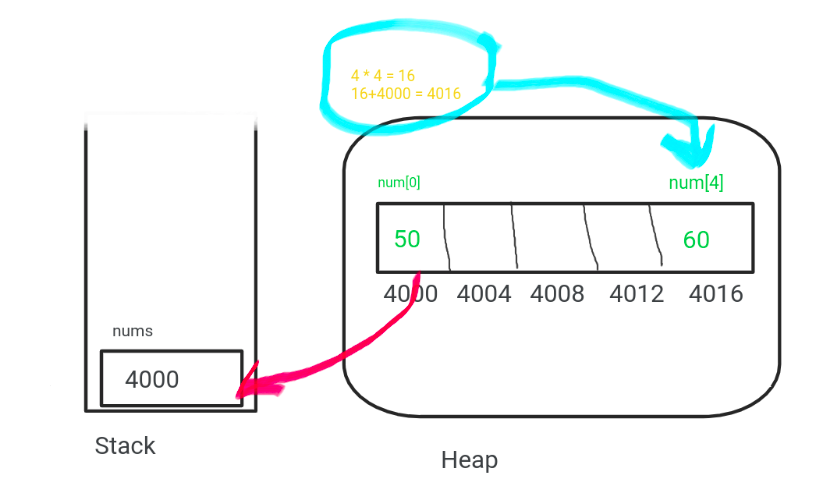
Ok, But Now what happen when we allocate memory:
nums = new int[5] // allocates memory for 5 integers
This will allocate memory for 5 integers, Each one has its own address. As we said above these allocated memory units are contiguous, hence they will be spaced out by the same distance.
Now, what will happen if we store values by index.
nums[0] = 50; // 0*4 = 0 => 0+4000 = 4000
num[4] = 60; // 4*4 = 16 => 16+4000 = 4016
- Arrays provide efficient element access because the elements are stored contiguously in memory.
- Accessing an element at a specific index is a constant-time operation (O(1)).
However, insertion and deletion of elements might be less efficient, especially if done frequently, as it requires shifting the elements in the array.
-
Inserting Elements at the End: O(1)
- Explanation: If there is space at the end of the array, appending an element is a constant-time operation.
-
Inserting Elements at the Beginning or Middle: O(n)
- Explanation: Inserting an element at the beginning or in the middle of an array requires shifting all subsequent elements one position to the right, which takes linear time.
Arrays are best suited for scenarios where:
- The number of elements is fixed or known in advance
- Fast, direct access to elements is required
- Memory efficiency is a priority
- Data structure complexity is minimal
collections refer to a framework that provides a set of classes and interfaces to store, manage, and manipulate groups of objects. The Java Collections Framework includes various data structures, such as lists, sets, maps, queues, and more. These collections efficiently store, retrieve, and process data, making it easier to work with aggregate data and perform common operations like searching, sorting, and iteration.
- The List interface represents an ordered collection of elements that allows duplicates.
- The List interface extends the Collection interface and adds methods to manipulate and access elements based on their index.
- Key features include ordered collection, allowing duplicates, and dynamic size changes.

- The ArrayList class implements the List interface.
- Can contain duplicate elements.
- maintains the insertion order.
- Non-synchronized. (not-thread safe).
- allow random access because the array works at index basis.
- Unlike arrays, arraylists can automatically adjust their capacity when we add or remove elements from them. (dynamic arrays).
in Java 8: to save memory consumption and avoid immediate memory allocation make The default capacity of an empty ArrayList is 0 and not 10. Once the first item is added, the DEFAULT_CAPACITY which is 10 is then used.
ArrayList grades = new ArrayList<>();
grades.add(90);
-now we will add another 9 elements:
for (int i=1; i<10; i++) {
grades.add(i+10);
}
What happens when you want to add the 11th element? How does ArrayList become resizable?
grades.add(10, 100);<br>
When you try to add a new element to an ArrayList in Java that has reached its default capacity of 10, the ArrayList will automatically resize itself to accommodate the new element.
Here's how it works:
-Check Capacity: The ArrayList checks if there is enough capacity to add the new element.
-Resize: If the current capacity is insufficient (which it is, in this case), the ArrayList will increase its capacity.
-Copy Elements: A new array with the increased capacity is created, and all the elements from the old array are copied into the new array.
-Add Element: The new element is added to the resized array.
The default behavior for resizing an ArrayList is to increase the capacity by 50%. So, if the current capacity is 10, the new capacity will be 15.
ArrayList<String> languages = new ArrayList<>();
// Add elements to ArrayList
languages.add("Java");
languages.add("Python");
languages.add("Ruby");
System.out.println("ArrayList: " + languages);
// add element on index 3
languages.add(3, "JavaScript");
System.out.println("ArrayList: " + languages);
// get the element from the arraylist
String lang = languages.get(1);
System.out.println("Element at index 1: " + lang);
// update value of the element
languages.set(2, "kotlin");
System.out.println("ArrayList: " + languages);
// remove element from index 1
languages.remove(1);
System.out.println("ArrayList after removing element: " + languages);
//get Size of array
System.out.println(languages.size());
The efficiency of common ArrayList operations:
-
Retrieval: Getting a specific element in the ArrayList is extremely fast with the ArrayList.get(i) method, where i is the element’s index.
-
Addition: Adding a new element to the ArrayList is usually extremely fast, as long as you are adding to the end and there is still room in the array. If the array is full, adding a new element requires more time because the array’s size first needs to be expanded.
-
Deletion: Deleting an element from the ArrayList is relatively slow, even though the actual deletion can be done quickly. This is because all elements after the deleted element need to be shifted one place to the left to fill the hole in the array left by the deletion.
The LinkedList class provides the functionality of the linked list data structure (use a doubly linked list to store the elements).

- contain duplicate elements.
- maintains insertion order.
- non synchronized.
- manipulation is fast because no shifting needs to occur.
- can be used as a list, stack or queue.
-
Prev - stores an address of the previous element in the list. It is null for the first element.
-
Next - stores an address of the next element in the list. It is null for the last element.
-
Data - stores the actual data.

When we remove Data1:
The Next pointer of data will be pointed to data2 Address and the prev pointer of data 2 will point address to Data.

-
Queue(FIFO) First Input First output: Enqueue - > add element to the end of the list. Dequeue -> retrieve and remove the first element of the list
-
Stack (LIFO) Last input first output: Push() Append the specified element to the end of the list pop() retrieve and remove the last element from this List.
// Creating list using the LinkedList class
List<Integer> numbers = new LinkedList<>();
// Add elements to the list
numbers.add(6);
numbers.add(9);
numbers.add(3);
numbers.add(3, 5);
System.out.println("List: " + numbers);
// add() method with the index parameter
numbers.add(3, 50);
System.out.println("Updated LinkedList: " + numbers);
// Access element from the list
int number = numbers.get(1);
System.out.println("Accessed Element: " + number);
// Using the indexOf() method
int index = numbers.indexOf(9);
System.out.println("Position of 9 is " + index);
// change elements at index 3
numbers.set(3, 100);
System.out.println("changed LinkedList: " + numbers);
// Remove element from the list
int removedNumber = numbers.remove(1);
System.out.println("Removed Element: " + removedNumber);
//get size
System.out.println("List Size: " + numbers.size());
/*LinkedList as Queue*/
Queue<String> names = new LinkedList<>();
// add elements
names.add("Ahmed");
names.add("Mohamed");
names.add("Mahmoud");
System.out.println("LinkedList: " + names);
// access the first element
String str1 = names.peek();
System.out.println("Accessed Element: " + str1);
// access and remove the first element
String str2 = names.poll();
System.out.println("Removed Element: " + str2);
System.out.println("LinkedList after poll(): " + names);
/*LinkedList as Deque*/
Deque<String> names = new LinkedList<>();
Deque<Integer> names1 = new LinkedList<>();
// add element at the beginning
names.add("Ahmed");
System.out.println("LinkedList: " + names);
names.addFirst("Mohamed");
System.out.println("LinkedList after addFirst(): " + names);
// add elements at the end
names.addLast("Mahmoud");
System.out.println("LinkedList after addLast(): " + names);
// remove the first element
names.removeFirst();
System.out.println("LinkedList after removeFirst(): " + names);
// remove the last element
names.removeLast();
System.out.println("LinkedList after removeLast(): " + names);
-
Retrieval: LinkedLists do not have an easy way to retrieve arbitrary elements. In the worst case, getting a specific element in the LinkedList therefore requires you to traverse the entire list to find the element you’re looking for.
-
Addition: Adding a new element to the LinkedList can be done in fast constant time if you are appending to the front or end of the list. If you want to insert a new element in an arbitrary position, you’ll need to spend more time traversing the list.
-
Deletion: Deleting an element from the LinkedList, like adding one, is fastest when deleting from the list’s front or end. However, deletion is slower when removing an arbitrary element.
-
ArrayList
- Time Complexity: O(1)
- Explanation: Retrieval is constant time because of direct access via array indexing.
-
LinkedList
- Time Complexity: O(n)
- Explanation: Retrieval is linear time because it requires sequential traversal of nodes.
-
ArrayList
- Average Time Complexity: O(1)
- Explanation: Adding an element to the end of an
ArrayListis generally very fast because it typically involves placing the element in the next available slot in the underlying array.- However, if the array is full and needs to be resized (which involves allocating a new array and copying elements), the time complexity for that specific operation can be O(n).
- On average, considering occasional resizing, the complexity is O(1).
-
LinkedList
- Time Complexity: O(1)
- Explanation: Adding an element at the end of a
LinkedListinvolves creating a new node and adjusting the pointers of the new node and the current tail node.- This operation is constant time, O(1), because the
LinkedListmaintains a reference to the tail node.
- This operation is constant time, O(1), because the
-
ArrayList
- Time Complexity: O(n)
- Explanation: Inserting an element at a specific position requires shifting all elements from the specified index onward one position to the right to make space for the new element.
- The time complexity of this shifting operation is O(n) in the worst case, where n is the number of elements in the
ArrayList. - If the underlying array is full and needs resizing, the cost of resizing is added to the insertion time.
- The time complexity of this shifting operation is O(n) in the worst case, where n is the number of elements in the
-
LinkedList
- Time Complexity: O(n)
- Explanation: To insert an element at a specific position, the list must be traversed to reach the desired index.
- Once the position is found, the operation involves creating a new node and updating the pointers of the adjacent nodes.
- The traversal requires O(n) time in the worst case, where n is the number of elements in the
LinkedList. The insertion itself is O(1) once the correct position is reached.
-
ArrayList
- Time Complexity: O(n)
- Explanation: Adding an element at the beginning of an
ArrayListrequires shifting all existing elements one position to the right to make space for the new element.- This operation involves moving n elements, resulting in a time complexity of O(n).
-
LinkedList
- Time Complexity: O(1)
- Explanation: Adding an element at the beginning of a
LinkedListinvolves creating a new node and adjusting the pointers of the new node and the current head node.- This operation is constant time, O(1), because it only involves updating a few pointers.
-
ArrayList
- Time Complexity: O(n)
- Explanation:
- Middle/Beginning Deletion: When deleting an element from the middle or beginning of an
ArrayList, all subsequent elements need to be shifted one position to the left to fill the gap left by the removed element. This results in a time complexity of O(n) in the worst case, where n is the number of elements in the list. - End Deletion: Deleting an element from the end of an
ArrayListis O(1) because no shifting is required. However, this scenario is less common in applications where deletions are spread throughout the list.
- Middle/Beginning Deletion: When deleting an element from the middle or beginning of an
-
LinkedList
-
Time Complexity:
- O(1) for deletions at the beginning or end.
- O(n) for deletions at arbitrary positions.
-
Explanation:
- Beginning Deletion: Deleting an element from the beginning of a
LinkedListis very efficient, as it only involves updating the head pointer to the next node. This is a constant-time operation, O(1). - End Deletion: Deleting an element from the end of a
LinkedListis also efficient because theLinkedListmaintains a reference to the tail node. The operation involves updating the tail pointer to the previous node, which is O(1). - Arbitrary Position Deletion: Deleting an element from an arbitrary position requires traversing the list to find the element, which takes O(n) time in the worst case. Once the element is found, updating the pointers to bypass the removed node is O(1), but the traversal dominates the overall time complexity, making it O(n).
- Beginning Deletion: Deleting an element from the beginning of a
-
- ArrayLists are best for cases where you will be retrieving elements (that is, reading from the array) more frequently than modifying the array.
- LinkedLists are best for cases where you will be modifying the list often, especially at the front or end of the list.
Set contains unique elements only.
- Store Elements by using a mechanism called hashing.
- Doesn’t maintain Insertion Order. Elements are inserted on the basis of their hashCode.
- The hashcode of an element is a unique identity that helps to identify the element in a hash table.
- Non Synchronized
- Contains unique elements only.
- HashSet is the best approach for search operation.
/* Hash Set*/
HashSet<String> languages = new HashSet<>();
// Using add() method
languages.add("Java");
languages.add("Python");
languages.add("Ruby");
languages.add("JavaScript");
languages.add("R");
languages.add("GO");
languages.add("JavaScript");
System.out.println("HashSet: " + languages);
// Using remove() method
boolean isRubyRemoved = languages.remove("Ruby");
System.out.println("Ruby lang is removed? " + isRubyRemoved);
System.out.println("HashSet: " + languages);
- HashSet uses HashMap internally to store data in the form of Key-Value pair.
- Elements are stored in the form of key-value pair.
- Whenever you create a HashSet object, one HashMap object associated with it is also created.
- where key will the actual element value and value will be the 𝑷𝑹𝑬𝑺𝑬𝑵𝑻 Constant.
-HashSet has default initial capacity of 16. -HashSet has default load factor of 0.75 or 75%.
-
The efficiency of a
HashSetin Java is primarily determined by its underlying implementation, which is based on aHashMap. -
Add (Insert) Operation:
- Average Case:
O(1) - Worst Case:
O(n) - Explanation: In the average case, the time complexity is constant
O(1)due to the efficient hashing mechanism. However, in the worst case, when many elements hash to the same bucket, it can degrade toO(n).
- Average Case:
-
Remove Operation
- Average Case:
O(1) - Worst Case:
O(n) - Explanation: Similar to the add operation, removing an element generally takes constant time
O(1). In the worst case, it can takeO(n)time if there are many hash collisions.
- Average Case:
-
Contains (Search) Operation
- Average Case:
O(1) - Worst Case:
O(n) - Explanation: Checking if an element is in the set usually takes constant time
O(1)due to the hash table's efficiency. In the worst case, if many elements collide in the same bucket, it can degrade toO(n).
- Average Case:
- provides functionalities of both the hashtable and the linked list data structure.
- Elements are stored in hash tables like HashSet.
- When you create a LinkedHashSet in Java, it internally uses a combination of a hash table and a doubly-linked list to store its elements
LinkedHashSet uses a hash table to quickly access elements based on their hash codes, enabling constant-time (O(1)) operations for adding, removing, and existence checks. Each element is placed in a specific bucket within the hash table, determined by its hash code.
Each element in the set is represented as a node in this linked list. The doubly-linked list allows the set to maintain the insertion order of elements.
- It is first hashed to find its bucket location in the hash table.
- If the bucket is empty, the element is added to the bucket, and a new node is created in the doubly-linked list to maintain insertion order.
- If the bucket is not empty, the set checks if the element already exists using its hash code.
- If the element is not found, it is added to the bucket, and a new node is created in the doubly-linked list to maintain insertion order.
- This approach ensures that LinkedHashSet maintains the order in which elements were inserted while preventing duplicates based on their hash codes.
- The use of the doubly-linked list provides predictable iteration order, meaning elements are returned in the same order as they were inserted.
However, due to the additional overhead of maintaining the linked list, LinkedHashSet may be slightly slower in terms of memory and insertion/deletion performance compared to a regular HashSet. Nevertheless, if you require a set with preserved insertion order and efficient access to elements, LinkedHashSet is a good choice.
LinkedHashSet<String> languages = new LinkedHashSet<>();
languages.add("Java");
languages.add("Python");
languages.add("Ruby");
languages.add("JavaScript");
languages.add("R");
languages.add("GO");
languages.add("JavaScript");
System.out.println("LinkedHashSet: " + languages);
- A LinkedHashSet is ideal when you need a collection that maintains insertion order without duplicates.
- It combines the advantages of a hash table (fast lookups) with a linked list (maintaining order).
- The object of the treeSet Class are sorted in ascending order.
- Contains Unique Elements Only.
- We can customize the sorting of elements by using the Comparator interface or comparable.
TreeSet<Integer> numbers = new TreeSet<>();
// Using the add() method
numbers.add(2);
numbers.add(10);
numbers.add(3);
numbers.add(4);
numbers.add(13);
System.out.println(numbers.first());
System.out.println(numbers.last());
System.out.println(numbers.headSet(10));
System.out.println(numbers.tailSet(10));
System.out.println("TreeSet: " + numbers);
/*HashMap*/
// create a hashmap
HashMap<String, Integer> languages = new HashMap<>();
// add elements to hashmap
languages.put("Java", 4);
languages.put("JavaScript", 10);
languages.put("Python", 7);
languages.put("R", 1);
System.out.println(languages);
// return set view of keys using keySet()
System.out.println("Keys: " + languages.keySet());
// return set view of values using values()
System.out.println("Values: " + languages.values());
// return set view of key/value pairs using entrySet()
System.out.println("Key/Value mappings: " + languages.entrySet());
// replace elements
languages.replace("R", 3);
System.out.println("After replace(): " + languages);
languages.put("R", 50);
System.out.println("After replace(): " + languages);
// iterate through keys only
System.out.print("Keys: ");
for (String key : languages.keySet()) {
System.out.print(key);
System.out.print(", ");
}
// iterate through values only
System.out.print("\nValues: ");
for (Integer value : languages.values()) {
System.out.print(value);
System.out.print(", ");
}
// iterate through key/value entries
System.out.print("\nEntries: ");
for (Map.Entry<String, Integer> entry : languages.entrySet()) {
System.out.print(entry);
System.out.print(", ");
}
//Creating TreeMap of numbers
TreeMap<String, Integer> numbers = new TreeMap<>();
// add elements
numbers.put("two", 2);
numbers.put("four", 4);
numbers.put("six", 6);
numbers.put("one", 8);
System.out.println("TreeMap of languages: " + numbers);
// Using entrySet()
System.out.println("Key/Value mappings: " + numbers.entrySet());
// Using keySet()
System.out.println("Keys: " + numbers.keySet());
// Using values()
System.out.println("Values: " + numbers.values());
// Using the firstKey() method
String firstKey = numbers.firstKey();
System.out.println("First Key: " + firstKey);
// Using the lastKey() method
String lastKey = numbers.lastKey();
System.out.println("Last Key: " + lastKey);
// Using firstEntry() method
System.out.println("First Entry: " + numbers.firstEntry());
// Using the lastEntry() method
System.out.println("Last Entry: " + numbers.lastEntry());
// Creating LinkedHashMap of languages
LinkedHashMap<String, Integer> languages = new LinkedHashMap<>();
// add Elements
languages.put("Java", 2);
languages.put("JavaScript", 9);
languages.put("Go", 3);
languages.put("Pascal", 1);
languages.put("Ruby", 8);
languages.put("R", 5);
System.out.println("LinkedHashMap: " + languages);
-
When working with a large collection where frequent insertion and deletion operations are expected, and random access is not a primary concern, what is the best choice ?
-
Suppose you are building an inventory management system for an online store. You need to keep track of the available stock of products. Each product has a unique identifier (product ID) and a corresponding quantity in stock. Which Collection can we use to solve this?
-
Suppose you are developing a user activity tracking system where you need to maintain the order of user actions. You want to store the actions in a collection while ensuring uniqueness?
-
In a social media application, there are millions of user posts generated every day. How can Java Collections help you handle and display the latest posts efficiently? Which collection would you use to maintain a sorted order of posts based on their timestamps?
-
You are developing a game, and you want to keep track of the top 10 players' high scores. Which Java Collection would be most appropriate for maintaining this leaderboard?
-
You are building a movie recommendation system. How would you store the movie data and user preferences using Java Collections? How would you efficiently retrieve and suggest movie recommendations based on a user's previous choices?
-
You are implementing a caching mechanism where each cached item must be unique and in the order of its insertion. Which Java collection would you use, and what advantages does it offer for this use case?
-
You need to store user session data where each user has a unique session ID, and you need quick retrieval by session ID. Which Java collection would you use, and what advantages does it offer for this use case?
-
You need to maintain a list of user comments on a blog post where duplicates are allowed and the order of insertion is preserved. Which Java collection would you use and why?
-
You need to implement a task scheduler where tasks are executed based on their priority. Which Java collection would you use, and what advantages does it offer for this scenario?