In this project, the metaheuristic algorithm is used for tuning machine learning algorithms hyper-parameters. A fraud detection project from the Kaggle challenge is used as a base project. The Project composed of three distinct sections.
- Metahurestic Algorithm (MA): Differential Evolution Algorithm (DEA) selected as an intelligent searching tool. The DE Algorithm is work on top of the ML Algorithm (in this case XGBoost) to find the best set of hyper-parameters.
- Machine Learning Algorithm: The XGBoost which is a powerful machine learning algorithm is selected and the DEA is applied to find the best set of hyper-paratmers.
- Final step: The Tuned ML algorithm is applied to the Fraud detection challange (training, validation, and test). The results was promising and showed 89% accuracy on test data.
In this notebook, we apply the Intelligent search methods like Differential Evolution Algorithm to find the best ML algorithm hyper-parameters. Previous options are using either predetermined or randomly generated parameters for the ML algorithms. Some of these searching methods are actually a simulation of Intelligent agents in nature like the folk of birds or school of fishes.
XGBoost_Hyperparameters_Tuning
|__ code/
| |__ xgboost-hyperparameters-and-ai.ipynb
|__ datasets/
|__ assets/
|__ figures/
|__ README.md
In this project the DE algorithm is selected as a intelligent searching tool. You may use your favorite one and replace it into the provided notebook in this project. The DE algorithm code borrowed from this work. We change these codes in another project here and make them to takes several objective functions simultaneously which would be more applicable to broad range of problems. The DE algorithm is a branch of evolutionary methods developed by Storn and Price (1997) and it is used to find the optimum solution for extensive, continuous domains. The DE algorithm begins with a population of random candidates and it recombines them to improve the fitness of each one iteratively using a simple equation.
Each random pair vectors (X1,X2) give a differential vector (X3 = X2 – X1). The weighted difference vector, X4 = F × X3, is used to perturb the third random vector, X5 using Eqation (X6 = X5 + X4) to achieve the noisy random vector, X6. The "F" term is called weighting or scaling factor and it is primarily within the range of 0.5 to 2. The weighting factor determines the amplification of differential variation among candidates. A crossover (CR) factor regulates the amount of recombinations between candidates. The CR is applied to the noisy random vector by taking the target vector into account to achieve the trial vector. The fitness of the trial vector is then compared to the target vector and it is replaced if it is a better fit. The DE algorithm repeats the mutation (weighting factor), recombination (crossover factor) and selection steps until a predetermined criteria is achieved. The four major steps for evolutionary methods are provided at the following figure. The DE algorithm, like any other metaheuristic algorithm, doesn't guarantee that an optimal solution is ever found (Atashnezhad et al., 2017).
Let's use the most Common ML Competition algorithm XGBoost for this project. You may choose a different one and replace it into the codes.
Let's use the TalkingData set which is available here on Kaggle.
Fraud challenge data set
|__ data/
| |__ ip
| |__ app
| |__ device
| |__ os
| |__ click_time
| |__ attributed_time
| |__ is_attributed
Two columns including attributed_time and click_time droped from data set and the rest are used for training a ML algorithm.
Several functions were defined at the begining of the project which help in writing codes more efficient. An example is provided at the following.
def read_train_test_data_balanced(address_train):
#Read Training data, all class 1 and add same amount 0
iter_csv = pd.read_csv(address_train, iterator=True, chunksize=10000000, parse_dates=['click_time'])
df_train_1 = pd.concat([chunk[chunk['is_attributed'] > 0] for chunk in iter_csv])
iter_csv = pd.read_csv(address_train, iterator=True, chunksize=10000000, parse_dates=['click_time'], skiprows = range(1,120000000), nrows=2000000)
df_train_0 = pd.concat([chunk[chunk['is_attributed'] == 0] for chunk in iter_csv])
#seperate same number values as train data with class 1
df_train_0 = df_train_0.head(len(df_train_1))
#Merge 0 and 1 data
df_train = Merge_data(df_train_1, df_train_0)
return df_trainUsing above function read all 1 values from the train data set and then add the same number of 0 and keep it.
df_train = read_train_test_data_balanced(address_train)
df_train.head(3)Now we do have a balance data set with an equal number of 0 and 1.
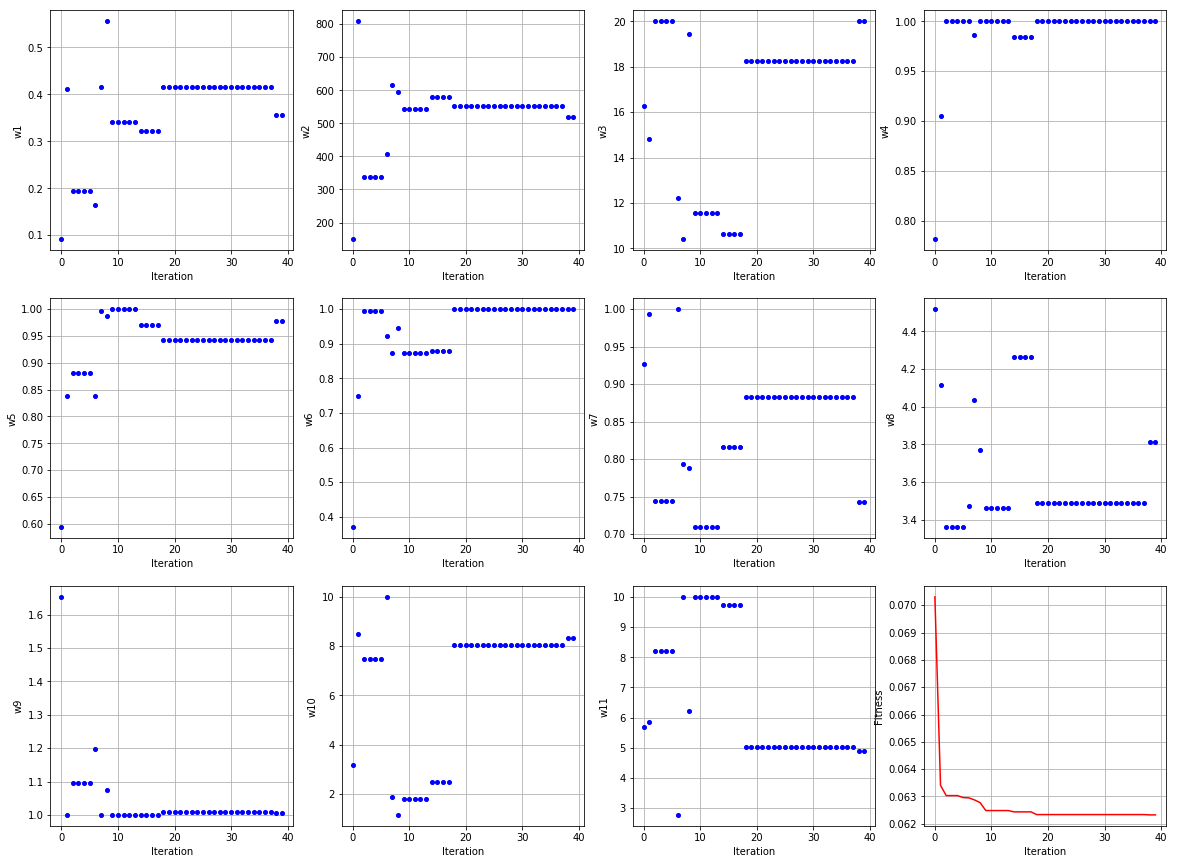
The DE algorithm along with a objective function are called to tune the XGBoost algorithm hyperparameters. The Objective fucntion uses XGBoost algorithm along with set of hyperparamters and returns the (1-accuracy) as a fitness value. The goal of DE algorithm is to find the hyperparamters that returns the lowest (1-accuracy) value. The hyperparameters ranges are selected at the following. Note that the fitness function does not take the effect of time into account. The user also can define different fitness function as he/she wishes. The best hyper XGBoost Algorithm hyper-parameters found as the follow:
eta 0.355402
max_leaves 520.000000
max_depth 20.000000
subsample 1.000000
colsample_bytree 0.978686
colsample_bylevel 1.000000
min_child_weight 1.000000
alpha 4.000000
scale_pos_weight 1.000000
nthread 8.000000
random_state 5.000000
Name: 39, dtype: float64
Following plot shows the searching progress of agents in the space of solutions.
Now that the hyperparameters were found, they are fed into the XGBoost algorithm and the XGBoost is applied for training and testing procedures respectively.
[0] train-auc:0.969407 valid-auc:0.968665
Multiple eval metrics have been passed: 'valid-auc' will be used for early stopping.
Will train until valid-auc hasn't improved in 25 rounds.
[5] train-auc:0.975196 valid-auc:0.97457
[10] train-auc:0.976906 valid-auc:0.975752
[15] train-auc:0.977917 valid-auc:0.97621
[20] train-auc:0.978799 valid-auc:0.976472
[25] train-auc:0.979276 valid-auc:0.976656
[30] train-auc:0.979782 valid-auc:0.976689
[35] train-auc:0.980202 valid-auc:0.97673
[40] train-auc:0.980494 valid-auc:0.976759
[45] train-auc:0.98077 valid-auc:0.976747
[50] train-auc:0.981003 valid-auc:0.976796
[55] train-auc:0.981273 valid-auc:0.97675
[60] train-auc:0.98154 valid-auc:0.976738
[65] train-auc:0.981777 valid-auc:0.97674
[70] train-auc:0.981938 valid-auc:0.976712
Stopping. Best iteration:
[49] train-auc:0.980968 valid-auc:0.976798The model accuracy on test data was found 89%.
- The click_time can potentially helps the ML algorithm to seperate between fraud clicks from those that are not. The same procedure can be done, taking the click_time into account.
- The time can be used as a separate parameter so the best hyper-parameters would result in faster solutions are selected. Without time there is a chance for the DE algorithm to increase the number of max_leaves and max_depth to the upper boundaries which results in a very time-consuming training procedure.