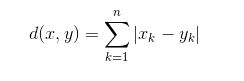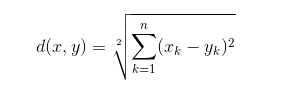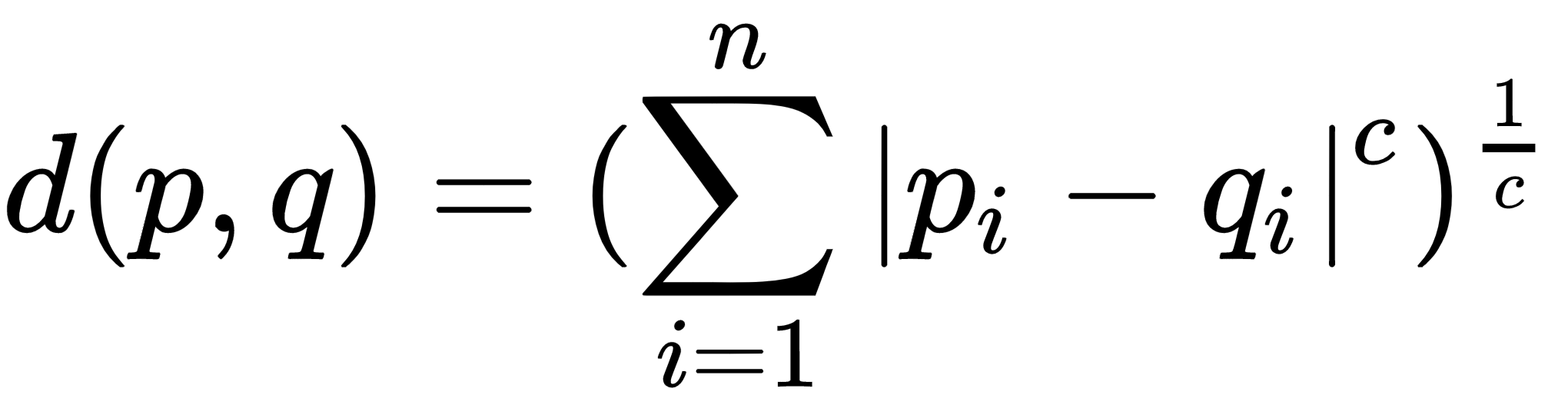In this lesson, we'll learn about various kinds of distance metrics that we can make use of in Data Science as a way to quantify similarity!
You will be able to:
- Calculate Manhattan Distance between 2 points
- Calculate Euclidean Distance between 2 points
- Compare and contrast Manhattan, Euclidean, and Minkowski Distance
In this section, we'll be focusing on a foundational Supervised Learning algorithm, K-Nearest Neighbors, or KNN for short. In order to understand how this algorithm works, we first have to understand some Distance Metrics, and we can use them to tell us how similar two objects are.
The assumption that distance-based classifiers like KNN are built on is that distance helps us quantify similarity. Objects that are more alike are more likely to be the same class. By treating each column in our dataset as a separate dimension, we can plot each data point that we have, and measure the distance between them!
You might remember learning about how to calculate the distance between two points on a cartesian plane from school. That's a certainly an important distance metric that we'll be using--however, there is more than one distance metric we can use, and all of them can be useful depending on the context of the problem. In this lesson, we'll learn how to calculate different distance metrics so that we have a tool to evaluate how similar or different data points are from one another when we begin exploring the KNN algorithm!
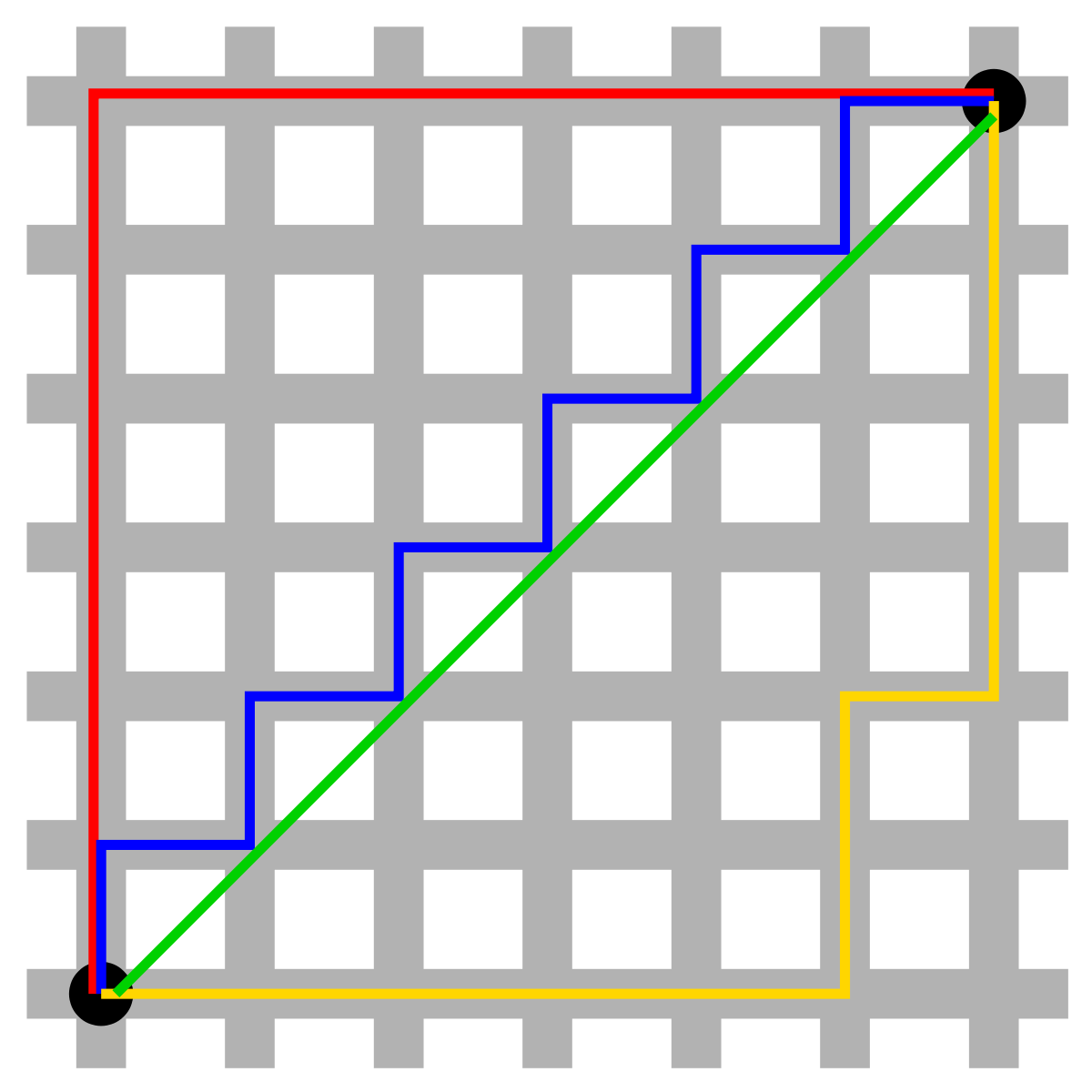
The first (and easiest) distance metric we'll cover is Manhattan Distance. Manhattan distance is aptly named, because it measures the distance from one point to another traveling along the axes of a grid. Take a look at the following image:
In this image, all the lines except for the green line measure the Manhattan Distance between the two points. You'll notice that if you start from the point in the bottom left corner of the grid and count the number of units moved in the X dimension (left and right) and the number of units moved in the Y dimension (up and down), the distance is the for the red, blue, and yellow lines.
The easiest way to remember Manhattan Distance is to use the analogy that provides this distance metric it's name--look at the picture above, but picture this grid as the famous grid of streets in Manhattan. If you were to take a taxi from point A (bottom left) to point b (top right), how many blocks east or west would the taxi have to travel? How many blocks north or south? How many blocks total? By calculating the total number of blocks we have to drive, we're actually calculating the Manhattan Distance between point A and point B.
So far, we've been talking about Manhattan Distance in a 2-dimensional space. However, all of the distance metrics we're going to learn can generalize to an n-dimensional space. For instance, in 3 dimensions, it's no harder to calculate the distance from one square on a Rubik's Cube to any other square--all we do is take into account how many squares we need to move towards or away from ourselves to measure depth, as well as left/right and up/down. Once we know the total units we need to move in each of these 3 dimensions, we just sum them to calculate the Manhattan Distance in 3 dimensions.
Here's the formula for Manhattan Distance:
Let's break this formula down a bit.
The left side of the equals sign just means "the distance between point x and point y".
The right side of the equals sign looks like it has a bit more going on, but don't let the mathematical notation scare you. In basic english, Manhattan Distance essentially just means "calculate the number of units you move in each distinct dimension, and then sum them all up". This is just saying the same thing with some mathematical notation.
The
Let's think about what this would look like in code. Let's assume that each point is stored as a tuple of values. If we wanted to calculate the distance between them, we can easily do this with a for loop!
point_1 = (2, 3, 5)
point_2 = (1, -1, 3)
manhattan_distance = 0
for i in range(3):
manhattan_distance += np.abs(point_1[i] - point_2[i]) # 7Anytime you see mathematical notation that includes the
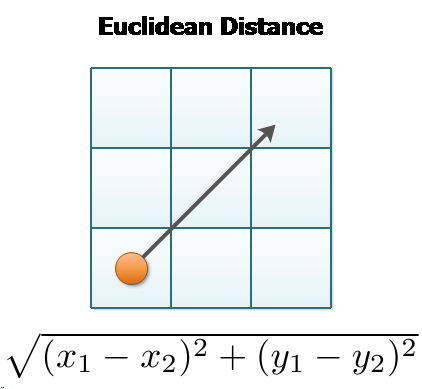
The next distance metric we'll cover is Euclidean Distance, although you may also have heard it referred to as Pythagorean Distance. The equation at the heart of this one is probably familiar to you:
In this case, that is:
Just as with Manhattan Distance, we can generalize this equation to
Let's take a look at the Euclidean Distance formula:
This is a straightforward equation--for dimension, we subract one point's value from the other's to get the length of that "side" of the triangle in that dimension, square it, and add it to our running total. The square root of that running total is our Euclidean Distance.
NOTE: We use the analogy of sides of a triangle here for simplicity's sake, but if you think about it, that analogy doesn't really work with more than 2 dimensions, because we are capable of visualizing things past 3 dimensions. (DISCLAIMER: Flatiron School takes no responsibility if you accidentally summon Cthulhu while trying to visualize multi-dimensional triangles.)
In python, we can easily calculate Euclidean Distance as follows:
point_1 = (2, 3, 5)
point_2 = (1, -1, 3)
euclidean_distance = 0
for i in range(3):
euclidean_distance += (point_1[i] - point_2[i])**2
euclidean_distance = np.sqrt(euclidean_distance)
euclidean_distance # 4.58257The final distance metric we'll talk about in this lesson is Minkowski Distance. This one is a bit technical, so try and bear with us here. Minkowski Distance is a generalized distance metric across a Normed Vector Space. A Normed Vector Space is just a fancy way of saying a collection of space where each point has been run through a function. It can be any function, as long it meets two criteria: the zero vector (just a vector filled with zeros) will output a length of 0, and every other vector must have a positive length.
Don't worry too much about the specifics of the mathematical definition above--on it's own, that's not something you should probably understand unless your a mathematician. Instead, we can gain an intuition for what Minkowski Distance actually measures another way. Both Manhattan Distance and Euclidean Distance are actually special cases of Minkowski Distance. Let's compare and contrast all 3 formulas and see if we can find the common thread:
Do you see it? It's the exponent! In this case, the function is just an exponent. If we were to define a value for the exponent, we could say that:
# Manhattan Distance is the sum of all side lengths to the first power
manhattan_distance = (length_side_1 + length_side2 + ... length_side_n)**1
# Euclidean Distance is the square root of the sum of all side lengths to the second power
euclidean_distance = np.sqrt((length_side_1 + length_side2 + ... length_side_n)*2)
# Minkowski Distance with a value of 3 would be the cube root of the sum of all side lengths to the third power
minkowski_distance_3 = np.cbrt((length_side_1 + length_side2 + ... length_side_n)**3)
# Minkowski Distance with a value of 5
mink_distance_5 = np.power((length_side_1 + length_side2 + ... length_side_n)**5, 1./5)You'll often see Minkowski Distance used as a parameter for any distance-based machine learning algorithms inside sklearn. This isn't a concept you'll have to worry about often, but it's definitely worth knowing about Minkowski Distance as a concept!
Knowing what we now know about Minkowski Distance, and its two special cases, Manhattan and Euclidean Distance, think about how you could write a generalized distance function that can calculate any of these, because it's exactly what we'll be doing in our next lab!