A repository containing different models that might work in effectively modeling Genshin pity (and, to a greater extent, pity on other miHoYo and gacha games).
There are actually quite a few problems to the approaches that have been used for pity in the past. For one, there is not convincing evidence to conclude that, indeed, there is a soft pity system. For another, these websites do not show the models they have used to conclude that there is soft pity. The aim of this repository is to refute some of the claims being made about the overall pity system.
The most important goal of this is replicability - that is, someone should be able to replicate what I did on their machine to attempt to model the observations that these websites might have seen.
An example of one of many charts showing the distribution of 5-star drops for the character banner. Source: Paimon.moe (MIT license)The above is an example graph showing the distribution of all 5-star drops from 1-90. This chart can be a bit misleading, particularly the line. The chart claims to be showing the probability of all drops from 1-90. However, it is showing the average of where 5-star pulls fall, given a hard pity system. By definition, soft pity implies that the probabilities change with each pull, which may not be the case. Rather, the "soft pity" observed here may be a mirage, and generated purely by hard pity. The data is also not representative of all Genshin Impact players, being only representative of all the users who visited that specific website. Confirmation bias may also be at play; a player who claims to observe "soft pity" may be more likely to submit their data to a website that shows what they claim.
The most that can be said for the above chart (and similar) is that the data (which is modeling a binomial distribution for pity counters up to 89) is approximately normal.
This repository requires Node.js to be installed on your machine. Download or clone the repository using git clone to get started after installing Node.js.
Several parameters are able to be adjusted in the files that allow you to collect different sample sizes as well as experiment with different probability distributions. The default sample size provided by this repository is 1048575, largely because Excel does not allow more than 1048576 rows, and this allows a file with 1048576 lines to be generated that can then be copied into Excel.
A model Excel spreadsheet is provided in this repository to allow you to quickly analyze the drops generated by the simulation. Useful stats you will get include average (including conditional) probabilities (similar to the chart above), where each rarity tends to fall, and, for the entire sample, which outcomes are most common.
This model simulates the gacha drops in a very simple manner: 4-star pity is triggered on the 10th pull, and 5-star pity is triggered on the 90th pull (for character banner) and 80th pull (for weapon banner). This is an absolute minimum as to achieve any less than this would be to depart from the pity system.
This model simulates the gacha drops in a similar manner as the minimum. 4-star pity is still triggered on the 10th pull, but 5-star pity is triggered on the 9th 4-star guarantee (for character banner) and 8th 4-star guarantee (for weapon banner), awarding a 5-star instead of a 4-star.
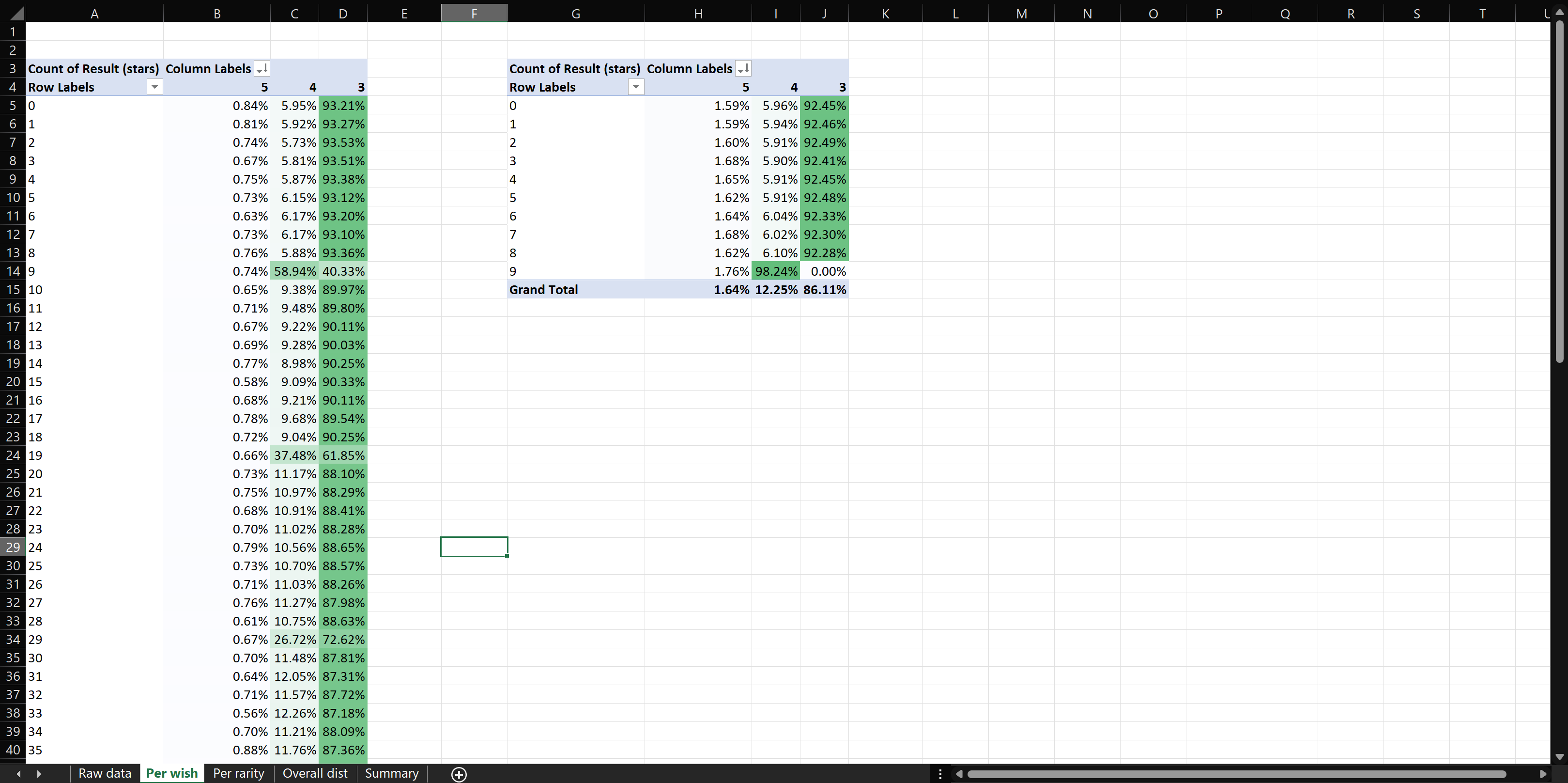
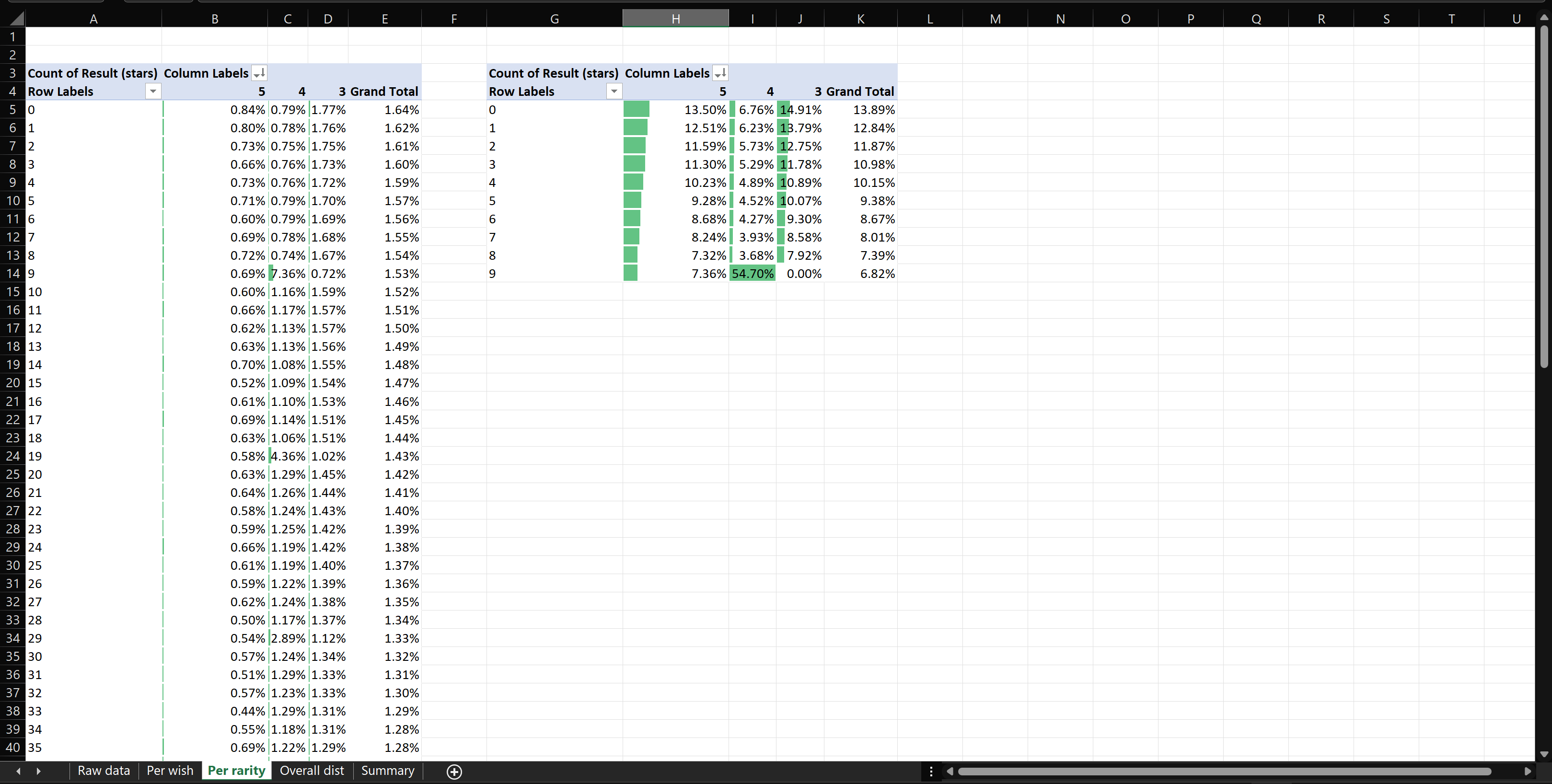
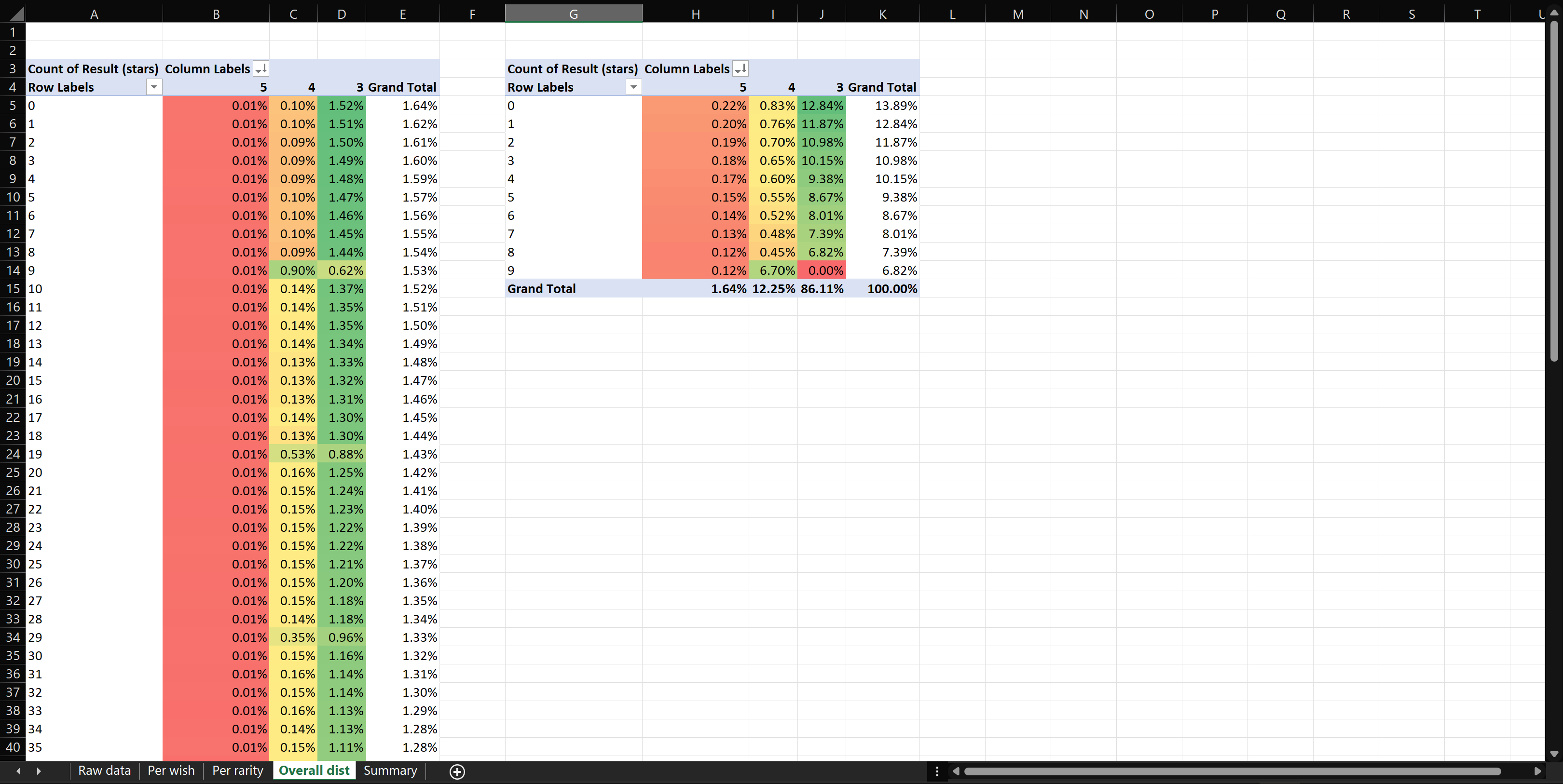
The attached spreadsheet has five different tabs to help analyze the results of your simulation (or a similar simulation). For each of the tabs "Per wish", "Per rarity", and "Overall dist", the right chart shows 4-star pities, while the left chart shows 5-star pities.
This is where you paste your raw data from the simulation. Delete all the rows except the first row, then select cell A1, and paste your data. You may need to refresh the spreadsheet (by going to Data > Refresh all) for all the charts to be refreshed.
The other tabs contain pivottables. The last tab contains a 5-number summary and the mean, median and mode for your data, as well as a tool to visually compare the average rarity based on your data to the expected rarity based on the five-number summary. The spreadsheet does not build confidence intervals or significance tests.
This tab contains conditional probabilities. The top of the charts is pretty straightforward, however, remember to mention that these probabilities are averages. All the other probabilities are conditional ("Probability of B given A") probabilities.
- Example: "On average, the probability of getting a 4-star given I did not get a 5-star on pulls 0-8 (respective to 5-star pity) is 58.94%."
- Another example: "On average, the probability of getting a 5-star given I did not get a 4-star on pulls 0-8 (respective to 4-star pity) is 1.76%"
This tab contains distributions by rarity (i.e. which pity numbers each wish is likely to fall at). These charts are best read as the proportion of drops that will fall on each pity counter.
- Example: "For 5-star pity, 7.36% of my 4-star drops happen on pull #9 (10th pull)"
This tab contains the average distribution of all of the data. Each cell shows the proportion of the data that have a specified rarity and are on a specified drop.
- Example: "0.62% of my data are 3-stars on pull #9 for 5-star pity."
This tab contains a summary of the entire data, as well as a tool for computing expected value given the average rates advertised by miHoYo. For character wishes, that would be (in order of increasing rarity) 85.4%-.13%-1.6%. For weapon wishes, that would be (in order of increasing rarity) 83.65%-14.5%-1.85%.
Fill in the data to get the expected value and standard deviation. A significance test can then be performed by calculating the appropriate test statistic and determining the probability that a mean or proportion is observed that is n standard deviations away from the population mean. A confidence interval can also be built with this method.
None of these simulations may be representative of the actual data. The average rates advertised by miHoYo mean that if infinitely many trials are conducted using miHoYo's gacha algorithm (which no one except the designers know), then on average the drop rates will be that which is advertised. The data generated by the simulations is finite, it may not be exactly miHoYo's gacha algorithm, and it gives different average rates than what miHoYo advertised.
If you notice any errors, please feel free to submit a pull request. Unfortunately, because I have real-life matters to tend to, I may not see your pull requests until after some time. You are also welcome to fork this repository and use it for any purpose, subject to the license terms.