BWsix/yee

Let us do our medieval mathematician friends a favor by finding out what the number 𝑒 is.

yee

Let us do our medieval mathematician friends a favor by finding out what the number 𝑒 is. Here, I'll be using C like what real computer programmers do. Python will also be used as a complementary tool since it has a builtin decimal module that can help us do some really high decimal precision calculations.

This is part of a bonus homework from the single variable calculus class I took here in my local college. I need to submit my code so I uploaded them here. In this homework, we were asked to write programs to find what number 𝑒 is using the following 3 methods.

Method A - Definition of 𝑒 as the Natural Logarithm Base

The number 𝑒 is the number in the domain of the natural logarithm that satisfies:

$$ \ln(e) = \int_{1}^{e} \mathrm{d}t = 1 $$

Intuition

We know that Riemann Sum can help us programatically find out area under a curve. Here, I'll be using a similar method to Riemann Sum to find out what 𝑒 is: only set the left bound and start doing mid-point sum with delta x until the accumulated area exceeds 1. When that happens, the right bound will be what we're looking for.

It's important to point out that when calculating slices of areas in Riemann Sum, two numbers are multiplied together, causing the precision to be doubled. Since C's double data type only has 15 decimal digits of precision, delta x can only has up to 7 decimal digits of precision. Anything more than that will cause underflow (assuming f(x) also has 7 decimal digits of precision).

Therefore, when we set delta x to be 10e-7, we'll get an estimation of 𝑒 that has a precision of 7 decimal digits. Which, to be fair, is good enough considering C's float data type only has 7 decimal digits of precision.

Implementation

This is how I implemented method a.

double area = 0.f;
double x = 1.f;
double delta_x = 10e-7;

for (; area < 1.f; x += delta_x) {
    double next_x = x + delta_x;
    double midpoint = (1.f / x + 1.f / next_x) / 2.f;
    area += midpoint * delta_x;
}

float e = x;

It would be nice to further optimize the code, but the approximation is already close enough (7 decimal digits to be exact), so I decided to leave it like that.

Performace

It takes us 10 million iterations just to get an estimation of 𝑒 with 7 decimal digits of precision. We can further generalize this precision-iteration ratio: to compute 𝑒 with n decimal digits of precision, we need to iterate 10 to the power of n times.

Method B - Definition of 𝑒 as a Limit

$$ 𝑒 = \lim\limits_{\delta \to 0} (1 + \delta)^{\frac{1}{\delta}} = \lim\limits_{n \to \infty} \left(1 + \frac{1}{n}\right)^{n} $$

A non-iterative method

If we were to estimate 𝑒 with this method, the code won't be iterative. To further explain, for method b we'll need to set a small enough delta for the formula on the left or a large enough n for formula on the right. Either way, we then only need to take the base to some power N.

An interesting relation between n and precision

With a little bit of help from python's builtin decimal module, I found that if we use the formula on the right, we'll get an interesting relation between N and number 𝑒's decimal precision: when N is 10 to the power of n, the estimated 𝑒 will (most of the time) have a decimal precision of n.

See for yourself by running yee.py with the following argument:

python yee.py b

First 15 rows of output:

10^n    correct decimal digits
1       1
2       2
3       3
4       4
5       5
6       6
7       7
8       8
9       9
10      10
11      11
12      11 <- oops
13      13
14      14
15      15

Implementation

It takes us only 2 lines of code to implement the formula on the right in C. Note that our n is 10e7, so the 𝑒 estimated will have a decimal precision of 7 digits.

double n = 10e7;
float e = pow(1.f + 1.f / n, n);

Surprisingly, the function pow() introduces small errors when n is larger than 10e6. So, in theory, the program above should give us 2.7182818, but it actually gives 2.7182817 instead.

Performace

Since it's a constant function, method b's performace is great.

Method C - Definition of 𝑒 as a Series

$$ 𝑒 = \sum_{{n=0}}^{\infty} \frac{1}{n!} $$

Intuition

Since in this definition, 𝑒 is defined by summing up things, we can easily convert this into a loop. We terminate the iteration when the difference between the accumulated 𝑒 from current step and the accumulated 𝑒 from the previous step is less than our target precision.

Implementation

size_t ITERATION_CAP = 1000;
double EPSILON = 10e-7;

double e = 0.f;
double prev_e = 0.f;
double one_over_factorial = 1.f;

for (size_t i = 1; i < ITERATION_CAP; i++) {
    prev_e = e;
    e += one_over_factorial;
    one_over_factorial *= 1.f / (double)i;
    if (fabs(e - prev_e) < EPSILON) {
        break;
    }
}

Performace

It only takes 11 iterations to get to our desired decimal precision (as usual, 7 since that's what C's float data type supports). I doubled the precision and this time, it takes 18 iterations. It's really performant even for higher precisions! I wonder if we can go even further with method c...

Infinitely precise representation of e

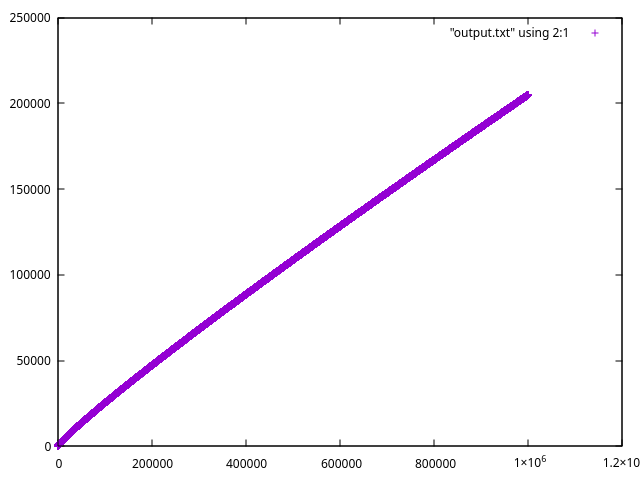
With python's builtin decimal module, I wrote a script and found that the precision of our approximation of e grows steadily with each iteration. In fact, it's even possible to get a precision of 1 million decimal digits with 200k iterations. The graph below help illustrate the relation between the number of iteration(x axis) and number of decimalprecision (y axis):

The graph above is generated by plotting method_c.1mil.txt with gnuplot. You can generate your own by running yee.py with the following argument:

python yee.py c

or

python yee.py c_optimized

Conclusion

For our medieval mathematician friends who do calculations by hand, method c is the only feasible way since it will only take them a few mathematical operations to get a good enough estimation of the number e. And the precision can be further increased by adding more terms to the calculated e in the future.

For us, if we only need a rough approximation (for example, 7 decimal digits of precision like what C's float data type supports), both method b and method c can get the job done under little to no time. Considering method b only takes 2 lines to implement, I'll definitely reccommend that to our medieval mathematician friends!

If we, for some reason, need a precision higher than 7 decimal digits, method b is out of town because of the error pow() introduces (assuming we're using C like a real computer programmer). Method c is perfect here since it's still very performant and can get us however many decimal digits of precision we want.

In yee.c, there's a function for benchmarking. Below is output of the benchmarking result for estimating e (7 decimal precision) 10,000 times. It showed us that method b and c are equally performant.

Benchmarking result for estimating e 10000 times:
Method  Time Taken(sec)
a       43.185198
b       0.000119
c       0.000218

That's about it! Hope our medieval mathematician friends can learn something from this report.

Quick Start

$ ./build.sh
$ ./yee -m a
$ ./yee -b abc 10000

or

$ cmake -S . -B build
$ cmake --build build
$ ./build/yee -m a
$ ./build/yee -b abc 10000