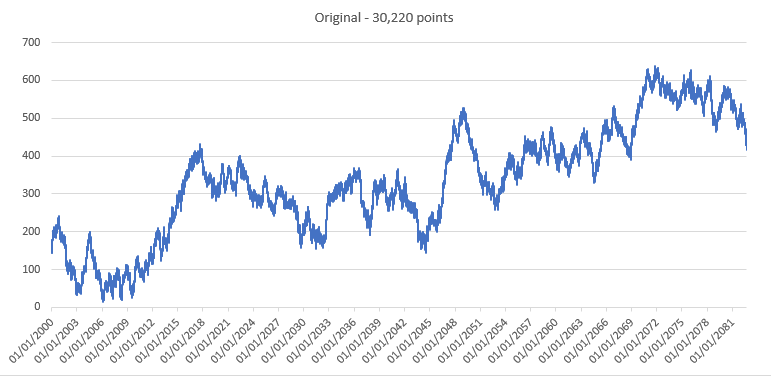
An algorithm that decimates a curve composed of line segments to a similar curve with fewer points.
The purpose of the algorithm is, given a curve composed of line segments (which is also called a Polyline in some contexts), to find a similar curve with fewer points. The algorithm defines 'dissimilar' based on the maximum distance between the original curve and the simplified curve (i.e., the Hausdorff distance between the curves). The simplified curve consists of a subset of the points that defined the original curve.source wiki
The pseudo-code is available on the wikipedia page. In this implementation, we use the perpendicular distance.
In order to make the algorithm faster, we consider the squared distance (and epsilon) so that we avoid using the absolute value and square root functions in the distance computation. We also split the computation of the distance so that we put in the 'for loop' only what is needed (the denominator is only computed once).
Perpendicular distance formula:
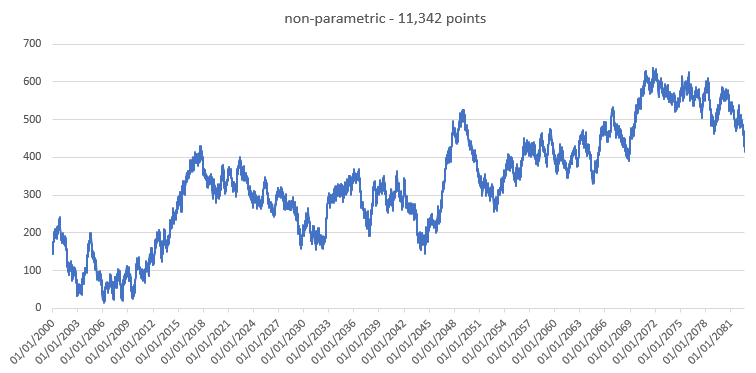
See A novel framework for making dominant point detection methods non-parametric by Prasad, Leung, Quek, and Cho.
3.1.2. Non-parametric adaptation of RDP
In the above method, at each step in the recursion, if the length of the line segment that is fit most recently on the curve (or sub-curve) is s and the slope of the line segment is m, then using Eq.(4), we compute dmax and use it in Eq.(7) as dtol=dmax. The pseudocodes of the original and the modified methods are given in Fig. 3 and the changes are highlighted for the ease of comparison. As a consequence of theproposed modification, the original method does not require any control parameter and adaptively computes the suitable value of dtol automatically.