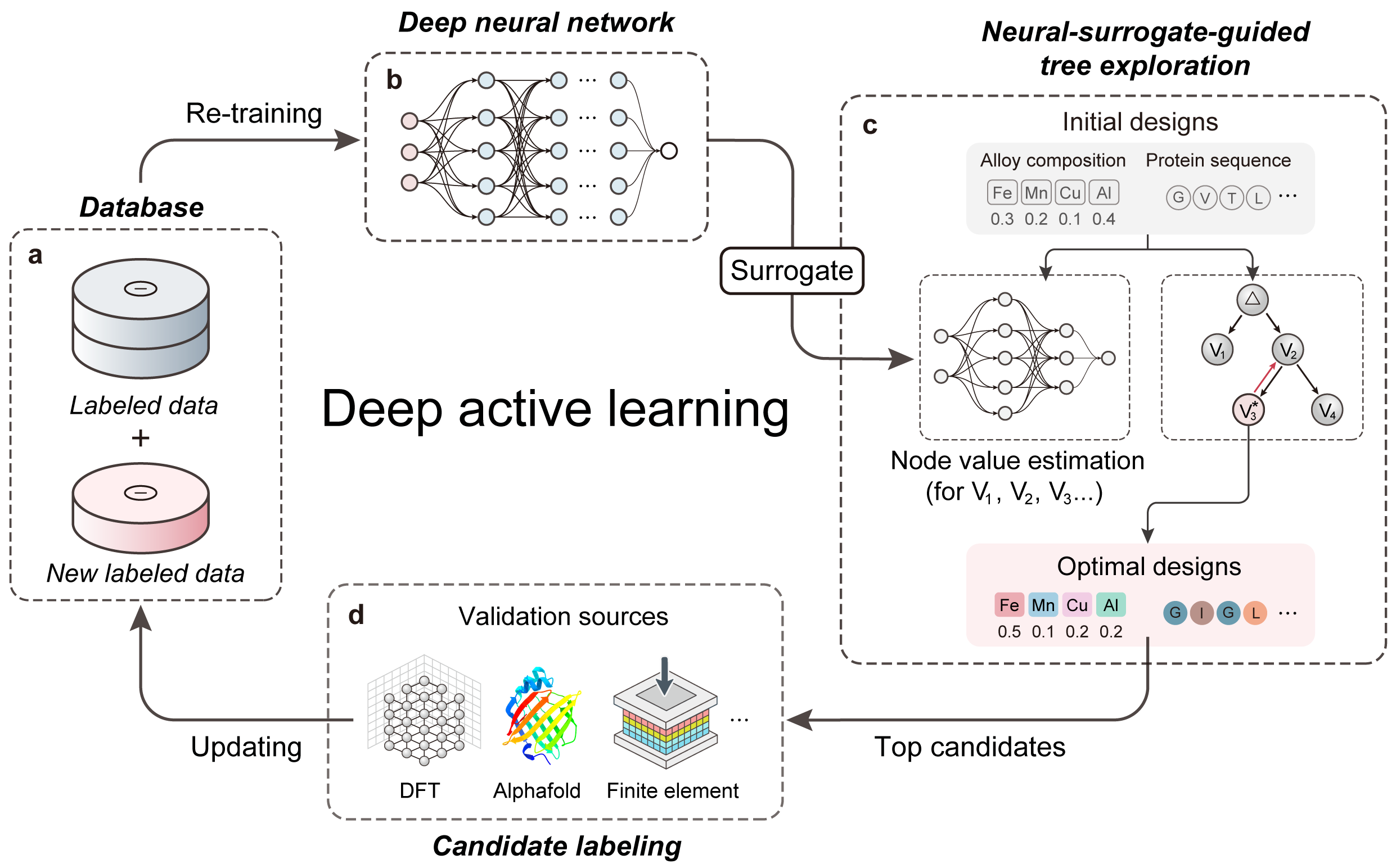
DANTE is a deep active learning pipeline that combines deep neural surrogate models and a novel tree search explorationalgorithm to find superior solutions in high-dimensional complex problems characterized by limited data availability and non-accumulative objectives.
For more details, please refer to our paper.
DANTE requires python>=3.10. Installation of TensorFlow and Keras with CUDA support is strongly recommended.
To install DANTE, run:
pip install git+https://github.com/Bop2000/DANTE.gitAlternatively, you can clone the repository and install it locally:
git clone git@github.com:Bop2000/DANTE.git
cd DANTE
pip install -e .To run tests for DANTE, execute the following command in the project root directory:
python -m pytest -m "not slow"Here's a minimal example of how to use DANTE:
import numpy as np
from dante.obj_functions import Ackley
from dante.neural_surrogate import AckleySurrogateModel
from dante.tree_exploration import TreeExploration
from dante.utils import generate_initial_samples
# Define parameters
NUM_DIMENSIONS = 20
NUM_INITIAL_SAMPLES = 200
NUM_ACQUISITIONS = 1000
SAMPLES_PER_ACQUISITION = 20
# Initialise the objective function and surrogate model
obj_function = Ackley(dims=NUM_DIMENSIONS)
surrogate = AckleySurrogateModel(input_dims=NUM_DIMENSIONS, epochs=500)
# Generate initial samples
input_x, input_y = generate_initial_samples(
obj_function, num_init_samples=NUM_INITIAL_SAMPLES, apply_scaling=True
)
# Main optimisation loop
for i in range(NUM_ACQUISITIONS):
# Train surrogate model and create tree explorer
trained_surrogate = surrogate(input_x, input_y)
tree_explorer = TreeExploration(func=obj_function, model=trained_surrogate, num_samples_per_acquisition=SAMPLES_PER_ACQUISITION)
# Perform tree exploration to find promising samples
new_x = tree_explorer.rollout(input_x, input_y, iteration=i)
new_y = np.array([obj_function(x, apply_scaling=True) for x in new_x])
# Update dataset with new samples
input_x = np.concatenate((input_x, new_x), axis=0)
input_y = np.concatenate((input_y, new_y))
print(f'number of data is {len(input_y)}')
print(f'current best y value is {input_y.max()}')
# Check for convergence
if np.isclose(np.array([obj_function(x, apply_scaling=False, track=False) for x in input_x]).min(), 0.0):
print(f"Optimal solution found after {i+1} iterations.")
break
# Print results
best_index = np.argmax(input_y)
print(f"Best solution: {input_x[best_index]}")
print(f"Best objective value: {obj_function(input_x[best_index], apply_scaling=False, track=False)}")To incorporate your own function into DANTE, please encapsulate it within a class as demonstrated below. You can find several examples in the obj_functions.py file for reference.
@dataclass
class myFunction(ObjectiveFunction):
dims: int = 10
turn: float = 0.1
name: str = "my_function"
def __post_init__(self):
self.lb = -5 * np.ones(self.dims) # Define the lower bounds for each dimension of the problem
self.ub = 5 * np.ones(self.dims) # Define the upper bounds for each dimension of the problem
self.tracker = Tracker("my_function") # Initialise a tracker to monitor the function's performance
def scaled(self, y: float) -> float: # Define a scaling function for better surrogate training
return 100 / (y + 0.01)
def __call__(self, x: np.ndarray, apply_scaling: bool = True) -> float:
x = self._preprocess(x)
y = some_function(x) # Define your function here
return y if not apply_scaling else self.scaled(y)The source code is released under the MIT license, as presented in here.