RIS components

This is a python project for RIS(reconfigurable intelligent surface) simulations.

related works

My first paper Link to my paper / Pdf to my paper:

[1] X. Guo, Y. Chen and Y. Wang, "Learning-based Robust and Secure Transmission for Reconfigurable Intelligent Surface Aided Millimeter Wave UAV Communications," in IEEE Wireless Communications Letters, doi: 10.1109/LWC.2021.3081464.

DDPG structure

Refer to the following code on github:
$\qquad$ a. tf-agent this is the easiest way the use the official RL(reinforcement learning) api.
$\qquad$ b. open source RL api using tensorflow: (coming soon) $\qquad$ c. DDPG structure refters to [3](pdf). There has already been some works on the combination of the DDPG and the RIS [4](pdf)

RIS simulation Refer to the paper Link to this paper / Pdf to this paper. This paper provide a simulation code in matlab, we refer to this project to provide a python version.

[2] E. Basar and I. Yildirim, "SimRIS Channel Simulator for Reconfigurable Intelligent Surface-Empowered Communication Systems," 2020 IEEE Latin-American Conference on Communications (LATINCOM), 2020, pp. 1-6, doi: 10.1109/LATINCOM50620.2020.9282349.

What this project aims ?

This project aims to redo the simulations shown in the paper below Link to this paper:

[3] Zhang, Zijian, et al. "Active RIS vs. Passive RIS: Which Will Prevail in 6G?." arXiv preprint arXiv:2103.15154 (2021).

Specifically, in this project we will simulate the active RIS. And to maximum the universality, this project will provide modular simulation tool for RIS-aided system.

File structure

./cite

The cited paper for this project

./learning

The code to initialize the agents

$\qquad$ ./learning/official

$\qquad$ The offical RL agents api (tf-agent)

$\qquad$ ./learning/custom

$\qquad$ The third party open source RL agent api

RIS theory

this section mainly refers to [2] (SimRIS1.0) and [2.2] (SimRIS2.0).

RIS-Assisted LOS channels(SISO)

According to the plate scattering theory[2,(1)], the transmitted signal is captured by each RIS element, then rescattered to the medium in all directions. Focusing on he $n$-th RIS element, the captured power on it can be readily obtained as $$ P_{n}^{RIS}=\frac{P_tG_tG_e^{Tx}\lambda^2}{(4\pi)^2a_n^2} \tag{1} $$ where $P_t$ is the transmit power,$G_t$ is the transmit antenna gain in the direction of the $n$-th RIS element (or the RIS in general), $G_e^{Tx}$ is the gain of the corresponding RIS element in the direction of the transmitter (Tx), $\lambda$ is the wavelength, and $a_n$ is the distance between the transmitter and this element. The effective aperture of the $n$-th RIS element is $G_{e}^{\mathrm{Tx}} \lambda^{2} /(4 \pi)$, and the power flux density incident on it given by $P_{t} G_{t} /\left(4 \pi a_{n}^{2}\right)$. Then the captured power is re-radiated to the medium with an efficiency factor $\epsilon$, which in [2] is assumed to be unity.

The captured power at the receiver (Rx) is obtained as

$$ P_{n}^{\mathrm{Rx}}=\frac{P_{n}^{\mathrm{RIS}} G_{e}^{\mathrm{Rx}} G_{r} \lambda^{2}}{(4 \pi)^{2} b_{n}^{2}}=\frac{P_{t} G_{t} G_{r} G_{e}^{\mathrm{Tx}} G_{e}^{\mathrm{Rx}} \lambda^{4}}{(4 \pi)^{4} a_{n}^{2} b_{n}^{2}}\tag{2} $$

where $G_r$ is the receive antenna gain in the direction of the $n$-th RIS element and $G_{e}^{\mathrm{Rx}}$ is the gain of the corresponding RIS element in the direction of the receiver. For the same scenario, let us consider the radar range equation given by

$$ P_{r}=\frac{P_{t} G_{t} G_{r} \lambda^{2} \sigma_{\mathrm{RCS}}}{(4 \pi)^{3} a_{n}^{2} b_{n}^{2}} \tag{3} $$

where $\sigma_{\mathrm{RCS}}=4 \pi A^{2} / \lambda^{2}$ is the radar cross section (RCS, in $m^2$) of the RIS element with $A$ being its physical area. (2) and (3) are actually the same, given $\sigma_{RCS} =\lambda^{2} G_{e}^{2} / 4 \pi$.

Let's assum the parameters as:

Parameter
$P_t = 0\ \text{dBW}$
$G_t= G_r = 1\ (0\ \text{dBi})$
$ G_{e}=\pi\ (5\ \mathrm{dBi})$ (Reference)[2-9]

Then the received power through $n$-th RIS element is: $$ P_{n}^{\mathrm{Rx}}=\frac{G_{e}^{2} \lambda^{4}}{(4 \pi)^{4} a_{n}^{2} b_{n}^{2}}\tag{4} $$ The total path loss is: $$ L_{n}=L_{n, 1} \times L_{n, 2}=\frac{G_{e} \lambda^{2}}{(4 \pi)^{2} a_{n}^{2}} \times \frac{G_{e} \lambda^{2}}{(4 \pi)^{2} b_{n}^{2}}\tag{5} $$ In general, the received signal at the receiver is: $$ y=\left(\sum_{n=1}^{N} \sqrt{P_{n}^{\mathrm{Rx}}}\left(\alpha_{n} e^{j \phi_{n}}\right) e^{-j k\left(a_{n}+b_{n}\right)}\right) x\tag{6} $$ Where $\alpha_n$ and $ \phi_n$ respectively stand for controllable magnitude and phase response of the nth element, $k=2 \pi / \lambda$ is the wave number, and $x$ is the transmitted signal. . One can easily observe from (6) that the received signal power can be maximized by adjusting RIS element phases as $\phi_{n}=k\left(a_{n}+b_{n}\right)$. Finally, it is worth noting that the direct link between Tx and Rx can be incorporated into the model by $$ y=\left(\sum_{n=1}^{N} \sqrt{P_{n}^{\mathrm{Rx}}}\left(\alpha_{n} e^{j \phi_{n}}\right) e^{-j k\left(a_{n}+b_{n}\right)}+\sqrt{P_{\mathrm{T}-\mathrm{R}}} e^{-j k d_{\mathrm{T-R}}}\right) x\tag{7} $$ Where $P_{\mathrm{T}-\mathrm{R}}=\lambda^{2} /\left(4 \pi d_{\mathrm{T}-\mathrm{R}}\right)^{2}$ and $d_{T-R}$ being the Tx-Rx distance.

RIS-Assisted channels(MIMO)[2.2]

Parameter	Meanings	Dimension
$N_{t}$	transmiter antennas number	${\mathbb R}$
$N_{r}$	receiver antennas number	${\mathbb R}$
$\mathbf{C}$	End-to-end channel matrix	${\mathbb C}^{N_r \times N_t}$
${\mathbf D}$	Direct channel matrix	${\mathbb C}^{N_r \times N_t}$
${\bf H}$	The matrix of channel coefficients between the Tx and the RIS	${\mathbb C}^{N \times N_t}$
${\bf G}$	The matrix of channel coefficients between the Tx and the RIS	$\mathbb{C}^{N_{r} \times N}$
${\bf \Phi}$	The response of the RIS array	$\mathbb{C}^{N \times N}$

$$ \mathbf{C}=\mathbf{G} \mathbf{\Phi} \mathbf{H}+\mathbf{D} $$

$$ R=\log {2} \operatorname{det}\left(\mathbf{I}{N_{r}}+\frac{P_{t}}{\sigma^{2}} \mathbf{C}^{H} \mathbf{C}\right) \mathrm{bit} / \mathrm{sec} / \mathrm{Hz} $$

channel generation

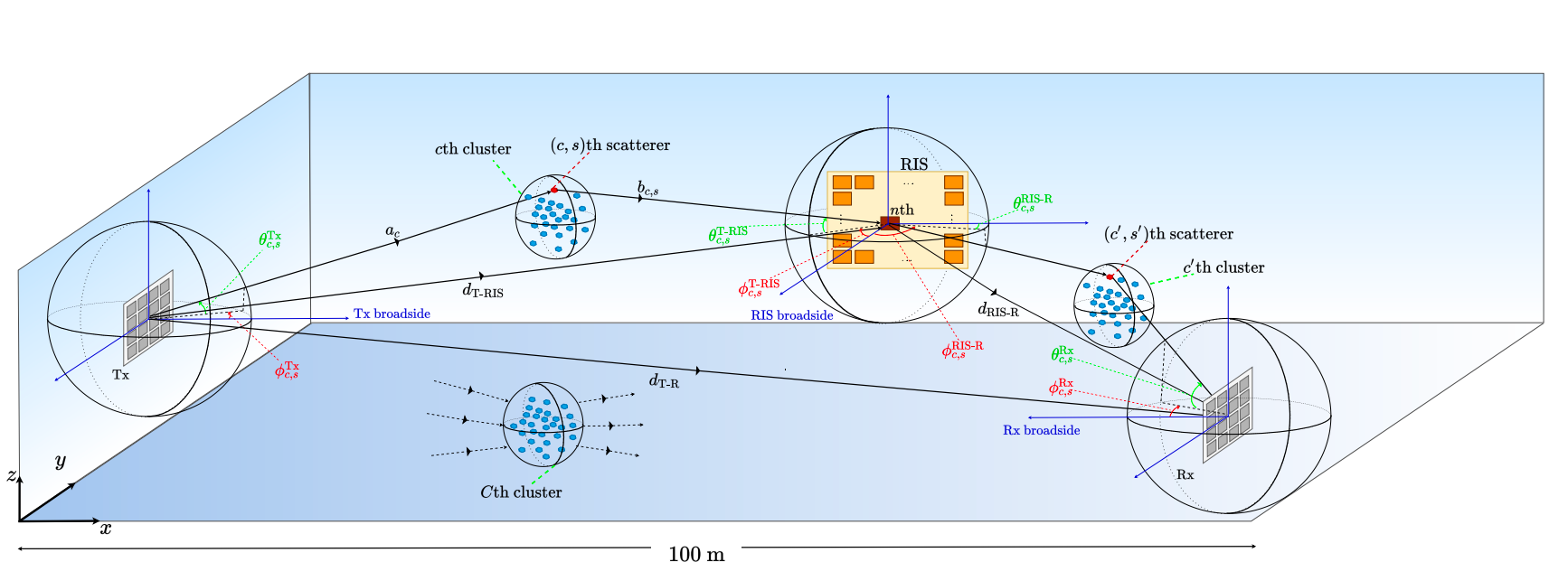
The detailed channel modeling can be seen in 3GPP 38.901 [5].

The basic idea to model the mmWave channel is to consider the channel under SISO senirio and then by multiplexing the array response, we can get the result of a mmWave channel under MIMO senirio.

The detailed SISO channel model can be found in [6]

path loss

cluster and sub-ray

array response

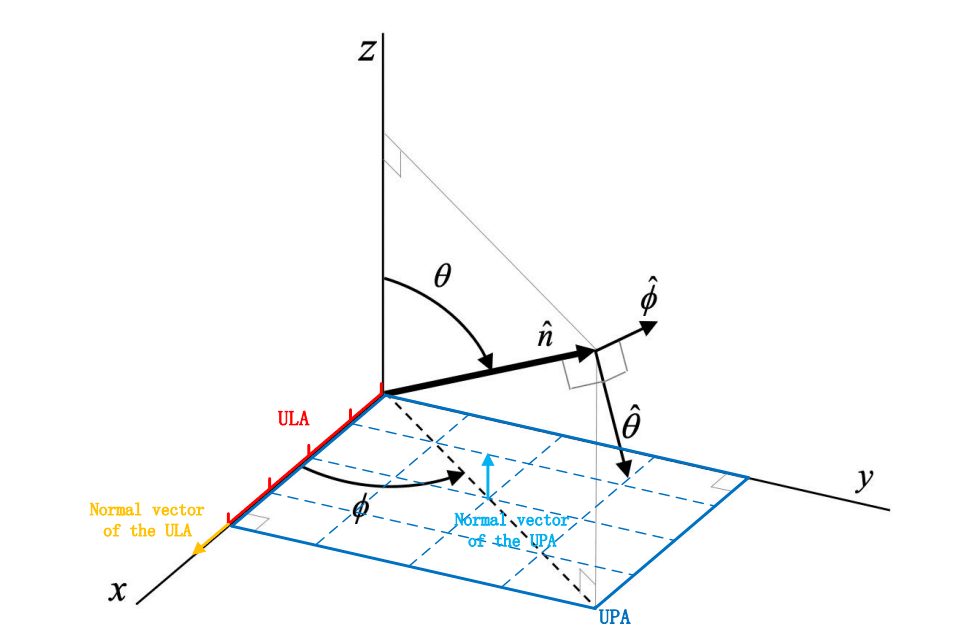
the defination of the AoA and AoD is shown below:

Others

coding platform: Win10 pro, anaconda3

nvidia driver: 466.47

cuda version: cuda_11.1.1_456.81_win10

cuddn version: cudnn-11.2-windows-x64-v8.1.1.33

tensorflow version: 2.4.0

python version: 3.8.10

Cited papers

[1](pdf) X. Guo, Y. Chen and Y. Wang, "Learning-based Robust and Secure Transmission for Reconfigurable Intelligent Surface Aided Millimeter Wave UAV Communications," in IEEE Wireless Communications Letters, doi: 10.1109/LWC.2021.3081464.

[2.0] E. Basar and I. Yildirim, "SimRIS Channel Simulator for Reconfigurable Intelligent Surface-Empowered Communication Systems," 2020 IEEE Latin-American Conference on Communications (LATINCOM), 2020, pp. 1-6, doi: 10.1109/LATINCOM50620.2020.9282349. note this and [2.1] is corresponding to the SimRIS1.0 which considers the SISO system

[2.1] E. Basar, I. Yildirim, “Indoor and Outdoor Physical Channel Modeling and Efficient Positioning for Reconfigurable Intelligent Surfaces in mmWave Bands“, ArXiv:2006.02240, May 2020

[2.2] E. Basar, I. Yildirim, “SimRIS Channel Simulator for Reconfigurable Intelligent Surfaces in Future Wireless Networks”, ArXiv:2008.01448, Aug. 2020.this is corresponding to the SimRIS2.0 which considers the MIMO system

[3](pdf) Lillicrap, Timothy P., et al. "Continuous control with deep reinforcement learning." arXiv preprint arXiv:1509.02971 (2015).

[4](pdf) Wang, Liang, et al. "Joint trajectory and passive beamforming design for intelligent reflecting surface-aided UAV communications: A deep reinforcement learning approach." arXiv preprint arXiv:2007.08380 (2020).

[5] 3GPP, “Study on channel model for frequencies from 0.5 to 100 GHz,” 3rd Generation Partnership Project (3GPP), Technical Specification (TS) 38.901, 01 2020, version 16.1.0. [6] E. Basar and I. Yildirim, “Indoor and outdoor physical channel modeling and efficient positioning for reconfigurable intelligent surfaces in mmWave bands,” Aug. 2020. [Online]. Available: https://arxiv.org/abs/2006.02240

Brook1711/RIS_components